3. Определители третьего порядка.

Пусть дана квадратная матрица третьего порядка

.

ОПРЕДЕЛЕНИЕ 4.1. Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число

(7)

Определитель третьего порядка обозначается символом

, (8)

где числа называются его элементами.

Индексы и у элемента показывают номера строки и столбца, на пересечении которых записан этот элемент.

Например, элемент расположен на пересечении второй строки ( ) и третьего столбца ( ).

Элементы образуют главную диагональ определителя, а элементы - побочную диагональ.

Определение 4.1 имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила. Так, согласно правилу треугольников необходимо:

1. вычислить с собственными знаками произведения элементов, лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали (рис.1);

2. найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками (рис.2);

3. найти общую сумму всех произведений.

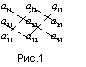
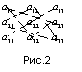
ПРИМЕР 4.1. .

Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (7).

Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,

Аналогично проверяется справедливость и других свойств.

Пусть дан определитель (8) третьего порядка.

ОПРЕДЕЛЕНИЕ 4.2. Минором элемента , где определителя третьего порядка, называется определитель второго порядка, полученный из данного вычеркиванием строки и столбца. Так, например, минор элемента есть определитель

, а минор элемента есть .

С помощью миноров определитель (7) можно записать в виде

.

ОПРЕДЕЛЕНИЕ 4.3. Алгебраическим дополнением элемента , где , называется минор этого элемента, взятый со знаком .

Согласно определению 4.3. имеем.

, где . (10)

Например,

,

и т.д.

ТЕОРЕМЕ 4.1. (Разложение определителя по элементам строки или столбца).

Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:

(11)

Проверим, например, справедливость равенства:

.

Согласно определениям минора и алгебраического дополнения получим

ТЕОРЕМЕ 4.2. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.

Для определенности выберем элементы первой строки и алгебраические дополнения элементов второй строки определителя. Составим сумму произведений и покажем, что эта сумма равна нулю.

Действительно,

Аналогично проверяется равенство нулю и всех других подобных сумм.

В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.

ПРИМЕР 4.2. Вычислить определитель .

Решение. Разложим определитель по элементам третьей строки.

ПРИМЕР 4.3. Вычислить определитель .

Решение. Прибавляя ко второй строке первую, умноженную на -8, получим . Раскладывая этот определитель по элементам второй его строки, найдем

.