17. Плоскость. Уравнение плоскости по точке и нормальному вектору.

Положение плоскости в пространстве вполне определяется заданием:

1. любых трех точек, не лежащих на одной прямой;

2. точки плоскости и вектора , перпендикулярного .

Н

z

айдем уравнение плоскости в каждом из перечисленных случаев ее задания. Пусть в пространстве дана точка и вектор (рис.21). Требуется найти уравнение плоскости , проходящей через точку перпендикулярно заданному вектору .

M₀

M

0

y

x

Выберем в произвольную точку и построим вектор

.

Рассмотрим два случая:

1. если точка , то   

 ; (34)

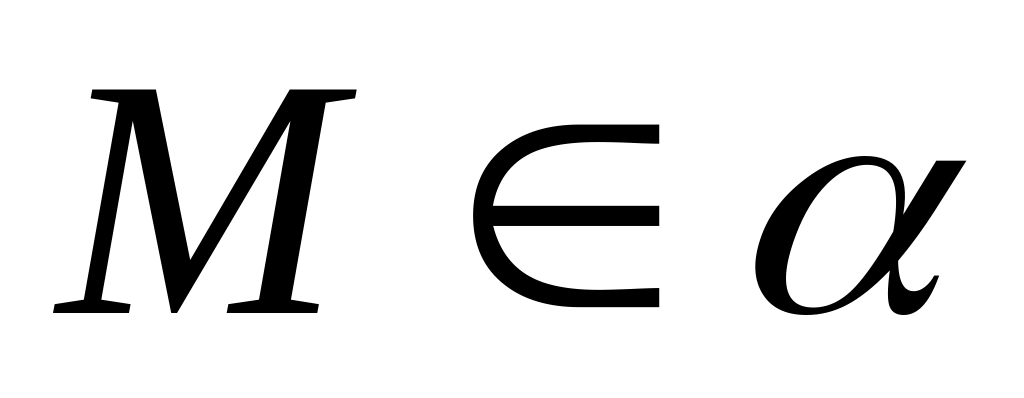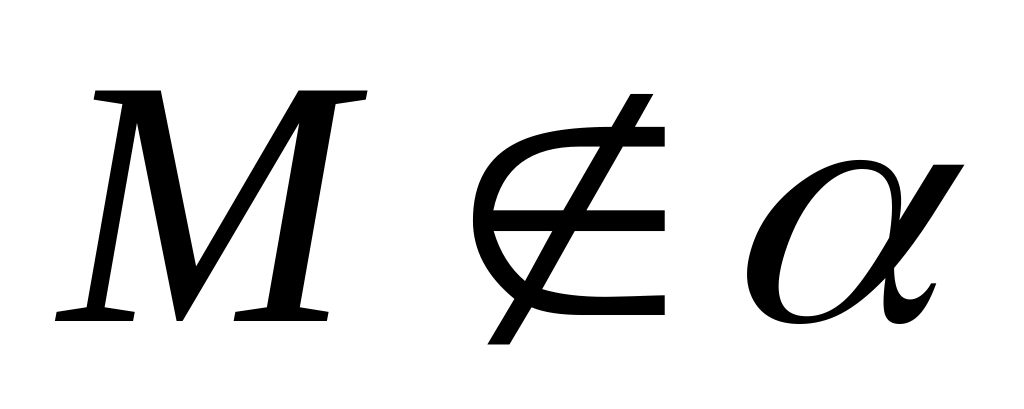2. если точка , то

   .

Из случаев 1) и 2) и определения уравнения поверхности следует, что уравнение (34) есть уравнение искомой плоскости . Уравнение (34) называется уравнением плоскости по точке и нормальному вектору. Вектор , перпендикулярный плоскости , называется нормальным вектором этой плоскости.

ПРИМЕР 16.1. Составить уравнение плоскости, проходящей через точку перпендикулярно вектору .

Решение. Уравнение искомой плоскости будем искать в форме . Полагая в уравнении (34) , получим .

18. Уравнение плоскости по трем точкам.

Пусть в пространстве даны три точки , , , не лежащие на одной прямой. Выберем в этом пространстве произвольную точку и построим три вектора , , .

z

M

M₂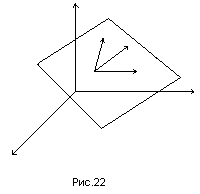

M₁

M₃

0

y

x

Предположим, что точка лежит на плоскости (рис.22), проходящей через заданные точки . Тогда векторы и лежат на этой плоскости. Следовательно, 

. (35)

Если же точка , то векторы и некомпланарны. Тогда и их смешанное произведение отлично от нуля. Согласно определению 15.1 уравнение (35) является уравнением искомой плоскости .

Заметим, что если расписать определитель (35), то полученное уравнение так же, как и уравнение (34), будет алгебраическим уравнением первой степени относительно трех переменных .

19. Общее уравнение плоскости.

Пусть задано произвольное алгебраическое уравнение первой степени относительно переменных

. (36)

Покажем, что уравнение (36) при любых допустимых значениях коэффициентов всегда является уравнением некоторой плоскости.

По условию по крайней мере один из коэффициентов или отличен от нуля. Тогда, предположив для определенности, что , перепишем уравнение (36) в форме

.

Сравнивая это уравнение с уравнением плоскости (34), найдем, что оно является уравнением плоскости, проходящей через точку и имеющей нормальный вектор . Следовательно, уравнение (36) является уравнением некоторой плоскости при любых допустимых значениях коэффициентов .

Итак, всякой плоскости в пространстве соответствует алгебраическое уравнение первой степени относительно трех переменных и всякому уравнению вида (36) соответствует плоскость. Уравнение (36) называется общим уравнением плоскости. Рассмотрим некоторые частные случаи этого уравнения:

1) . Тогда плоскость проходит через начало координат, так как точка принадлежит этой плоскости при любых значениях и ;

2) . Уравнение плоскости запишется в виде . Так как старшие коэффициенты и являются проекциями нормального к плоскости вектора , то вектор перпендикулярен этой плоскости. Но вектор перпендикулярен и координатной оси . Следовательно, рассматриваемая плоскость параллельна оси ;

3) если , то плоскость параллельна оси (доказать самостоятельно);

4) если , то плоскость проходит через начало координат и параллельна оси . Следовательно, плоскость проходит через ось ;

5) если , то  совпадает с плоскостью .

ПРИМЕР 18.1. Определить, перпендикулярен ли вектор плоскости .

Решение. Коэффициенты являются проекциями нормального вектора плоскости. Тогда, если вектор перпендикулярен заданной плоскости, то векторы и дожны быть коллинеарными. Согласно коллинеарности двух векторов проекции этих векторов должны быть иррациональными между собой. Но , следовательно, вектор не перпендикулярен данной плоскости.