
- •I. Алгебра.
- •Матрицы и их виды.
- •2. Операции над матрицами.
- •2.1. Равенство матриц.
- •2.2. Сложение матриц.
- •2.3. Умножение матрицы на число.
- •2.4. Умножение матриц.
- •Определители второго порядка.
- •Определители третьего порядка.
- •Определители n-го порядка.
- •Обратная матрица.
- •Системы линейных уравнений. Общие понятия.
- •Система n линейных уравнений с n неизвестными и ее решение матричным способом. Формулы крамера.
- •Решение системы линейных уравнений методом гаусса.
- •Плохо обусловленные системы линейных уравнений.
- •Скалярные и векторные величины.
- •Линейные опреции над векторами.
- •Угол между векторами. Проекция вектора на ось.
- •Линейная комбинация векторов. Базис.
- •Прямоугольная декартовая система координат.
- •Линейные операции над векторами, заданными в координатной форме.
- •Пройстейшие задачи аналитической геометрии.
- •Задачи определения расстояния между двумя точками.
- •Задача деления отрезка в данном отношении.
- •Скалярное произведение векторов.
- •Свойства скалярного произведения векторов.
- •Векторное произведение векторов.
- •Смешанное произведение векторов.
- •II. Элементы аналитической геометрии. Введение.
- •Плоская линия и ее уравнение в .
- •Прямая линия на плоскости. Уравнение прямой по точке и нормальному вектору.
- •Уравнение прямой по точке и направляющему вектору. Пусть на плоскости дана точка и вектор (рис.4).
- •Пусть прямые и даны уравнениями и . Требуется определить угол между ними. Предположим, что прямые не перпендикулярны и вычислим . Непосредственно из рис.9 найдем, что . Тогда
- •Общее уравнение прямой.
- •Кривые второго порядка. Окружность.
- •Эллипс.
- •Гипербола.
- •Парабола.
- •Уравнение кривых второго порядка с осями симметрии, параллельными осями координат.
- •Исследование уравнения кривой второго порядка, не содержащего члена с произведением текущих координат.
- •Неравенства второй степени относительно двух переменных.
- •Поверхности и линии в пространстве .
- •Плоскость. Уравнение плоскости по точке и нормальному вектору.
- •Уравнение плоскости по трем точкам.
- •Общее уравнение плоскости.
- •Угол между плоскостями.
- •20. Прямая в пространстве . Векторное, канонические и параметрические уравнения прямой.
- •Уравнение прямой по двум ее точкам.
- •Общие уравнения прямой.
- •Угол между двумя прямыми.
- •Прямая и плоскость в пространстве .
- •Угол между прмой и плоскостью.
- •Точка пересечения прямой с плоскостью.
- •Поверхности второго порядка.
- •Цилиндрические поверхнсоти.
- •Эллипсоид.
- •Эллиптический параболоид.
- •Однополостный гиперболоид.
- •Двуполостной гипрболоид.
Парабола.
ОПРЕДЕЛЕНИЕ 11.1. Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Выберем на плоскости
произвольную точку
![]() и произвольную прямую
и произвольную прямую
![]() ,
не проходящую через эту точку. Назовем
точку
фокусом, а прямую
директрисой. Обозначим расстояние от
точки
до прямой
через
,
не проходящую через эту точку. Назовем
точку
фокусом, а прямую
директрисой. Обозначим расстояние от
точки
до прямой
через
![]() и построим систему координат
так, как это изображено на рис.16.
и построим систему координат
так, как это изображено на рис.16.

Рис.16
Тогда фокус будет
расположен в точке
![]() ,
а директриса будет иметь уравнение
,
а директриса будет иметь уравнение
![]() .
.
Пусть точка
произвольная точка плоскости
.
Предположим, что точка
лежит на параболе. Тогда, по определению
этой кривой
![]() ,
где
,
где
![]()
.
Точка
.
Точка
![]() по построению имеет координаты
по построению имеет координаты
![]() .
Следовательно, равенство
запишется в виде
.
Следовательно, равенство
запишется в виде
![]() .
.
Освобождаясь от иррациональности, получим
![]() . (20)
. (20)
Пусть точка
не лежит на параболе. Тогда
![]() .
Следовательно, и
.
Следовательно, и
![]() .
.
Итак, согласно
определению 1.1 уравнения плоской кривой
уравнение (20) является уравнением искомой
параболы. Оно называется каноническим
уравнением параболы, а число
![]() называется ее параметром.
называется ее параметром.
Определим форму
параболы. В уравнение (20) переменная
входит в четной степени. Следовательно,
кривая симметрична относительно оси
.
При
![]() .
Значит, кривая проходит через начало
координат. При
.
Значит, кривая проходит через начало
координат. При
![]() ,
,
![]() ,
так как по условию
.
При
,
так как по условию
.
При
![]() существует, причем при увеличении
переменная
также увеличивается. По полученным
данным построим параболу (рис.16).
существует, причем при увеличении
переменная
также увеличивается. По полученным
данным построим параболу (рис.16).
Терминология. Точка называется фокусом параболы. Точка называется вершиной параболы. Прямая называется директрисой. Ось, на которой расположен фокус, называется фокальной осью. Расстояние от фокуса до директрисы называется параметром параболы.
Дополнение. Если фокальную ось параболы принять за ось , то уравнение параболы запишется в виде
![]() . (21)
. (21)
ПРИМЕР 11.1. Найти
фокус и уравнение директрисы параболы
![]() .
.
Решение. Так как
каноническое уравнение параболы имеет
вид
![]() ,
то
,
то
![]() .
Следовательно,
.
Следовательно,
![]() ,
а
,
а
![]() .
Фокус параболы расположен в точке
.
Фокус параболы расположен в точке
![]() .
Директриса имеет уравнение
.
Директриса имеет уравнение
![]() .
.
Уравнение кривых второго порядка с осями симметрии, параллельными осями координат.
Рассмотрим
предварительно одну из частных задач
преобразования системы координат. Пусть
на плоскости введены две прямоугольные
декартовы системы координат
и
![]() с центрами в точках
и
с центрами в точках
и
![]() и соответственно параллельными осями
координат (рис.17).
и соответственно параллельными осями
координат (рис.17).
 Рис.17
Рис.17
Пусть точка
в системе
имеет координаты
![]() .
Выберем на плоскости произвольную точку
и обозначим ее координаты через
.
Выберем на плоскости произвольную точку
и обозначим ее координаты через
![]() и
и
![]() в соответствующих системах
и
.
Поставим задачу установления формул
связи между координатами точки
в старой (
)
и новой (
)
системах координат. Очевидно, что в
системе
вектор
в соответствующих системах
и
.
Поставим задачу установления формул
связи между координатами точки
в старой (
)
и новой (
)
системах координат. Очевидно, что в
системе
вектор
![]() ,
вектор
,
вектор
![]() .
В системе
вектор
.
В системе
вектор
![]() .
.
Согласно правилу сложения векторов
![]() или
или
![]() (22)
(22)
Формулы (22),
связывающие между собой старые и новые
координаты точки плоскости, называются
формулами параллельного переноса
системы координат. Пусть теперь на
плоскости
задан эллипс с полуосями
и
,
центр которого находится в точке
![]() ,
а оси симметрии параллельны осям
координат
и
.
Требуется найти уравнение эллипса.
Введем новую систему координат
с помощью параллельного переноса системы
,
расположив ее начало координат в центре
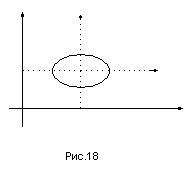
эллипса (рис.18). Тогда в новой системе
каноническое уравнение эллипса запишется
в виде
,
а оси симметрии параллельны осям
координат
и
.
Требуется найти уравнение эллипса.
Введем новую систему координат
с помощью параллельного переноса системы
,
расположив ее начало координат в центре
эллипса (рис.18). Тогда в новой системе
каноническое уравнение эллипса запишется
в виде
![]() .
Из (22) найдем, что
.
Из (22) найдем, что
![]() .
Тогда в заданной системе координат
уравнение эллипса примет вид
.
Тогда в заданной системе координат
уравнение эллипса примет вид
![]()
 . (23)
. (23)
y
y’
y0
0’
x’
0
x0
x
Уравнение (23) является уравнением эллипса с полуосями и , центром в точке и осями симметрии, параллельными координатным осям.
Решая аналогичным образом задачу относительно уравнения гиперболы с центром в точке , с осями симметрии, параллельными осям координат, с действительной полуосью, равной , мнимой, равной , получим уравнение
![]() . (24)
. (24)
Аналогично найдем, что уравнение параболы, ось симметрии которой параллельна оси абсцисс, вершина которой находится в точке , а ее параметр равен , имеет вид
![]() . (25)
. (25)
Если же ось параболы параллельна оси ординат, то
![]() . (26)
. (26)
