3. Сложение сил. Система сходящихся сил. Главный вектор системы сил. Разложение сил по двум и по трем направлениям.

Сложение сил, операция определения векторной величины R, равной геометрической сумме векторов, изображающих силы данной системы и называется главным вектором этой системы сил. С. с. производится по правилу сложения векторов, в частности построением многоугольника сил. Механический смысл величины R определяется теоремами статики и динамики. Так, если система сил, действующих на твёрдое тело, имеет равнодействующую, то она равна главному вектору этих сил. При движении любой механической системы её центр масс движется так же, как двигалась бы материальная точка, имеющая массу, равную массе всей системы, и находящаяся под действием силы, равной главному вектору всех действующих на систему внешних сил. Систе́ма сходя́щихся сил — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке. Задачи с системой сходящихся сил могут быть решены как аналитически, так и графически (методами графостатики). Главный вектор F'гл представляет собой геометрическую сумму всех сил, составляющих систему и перенесенных в центр приведения. Модуль главного вектора можно определить через проекции на координатные оси всех сил системы.

4. Проекция силы на ось и проекция силы на плоскость. Аналитический способ задания сил. Аналитический способ сложения сил.

Проекцией силы F на ось Ox называется скалярная величина F_x, равная произведению ее модуля F на косинус угла между силой и положительным направлением оси: F_x=F·cos.Проекция силы на ось:

• положительна, если угол-острый;

• равна нулю, если угол 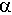- прямой ( сила перпендикулярна оси );

• отрицательна, если угол 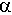- тупой.

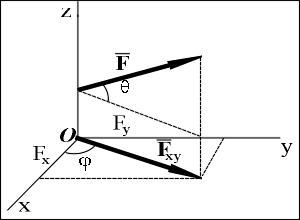
Проекцией силы F на плоскость Oxy называется вектор F_xy, заключенный между проекциями начала и конца силы F на эту плоскость. В отличие от проекции силы на ось, проекция силы на плоскость является векторной величиной и характеризуется не только числовым значением, но и направлением в плоскости Oxy. По модулю F_xy=F·cos, где- угол между векторамиF и F_xy. Проекция силы на плоскость используется, например, для нахождения проекций силы на оси, лежащие в этой плоскости (см. рис.): F_x=F_xy·cos; F_y=F_xy·sin.Аналитическое сложение сил основано на известной теореме векторной алгебры: проекция вектора суммы на ось равна алгебраической сумме проекций слагаемых векторов на ту же ось:

  Модуль (численное значение) главного вектора

Действие силы на твердое тело может вызвать вращательный эффект, который для плоской системы сил оценивается моментом силы относительно какой-либо точки О на плоскости (рис. 13):

;    ,

где h₁ и h₂  плечи сил и  относительно точки О.

5. Равновесие системы сходящихся сил. Теорема о трех силах. Понятие о статической определимости системы сил.

Равновесие системы сходящихся сил.Из законов механики следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инерции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.Отсюда получаем два важных вывода: 1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции». 2) Уравновешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравновешенных сил. Для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме.

1. Геометрическое условие равновесия. Так как равнодействующая R сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то R может обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой, т. е. когда многоугольник замкнется.

Следовательно, для равновесия системы, сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут.

1. Аналитические условия равновесия. Аналитически равнодействующая системы сходящихся сил определяется формулой

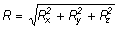
Теорема о трех силах. Если (абсолютно твердое) тело находится в равновесии под действием плоской системы трех непараллельных сил (т.е. сил, из которых хотя бы две непараллельные), то линии их действия пересекаются в одной точке. Доказательство. Пусть из трех сил F1, F2, F₃ , приложенных соответственно в точках А, В и С (рис.3), непараллельными являются F1 и F2. Продолжим линии их действия до пересечения в точке О и перенесем в эту точку обе силы. Очевидно, система {F1, F2} эквивалентна , а эта последняя уже имеет равнодействующую R. Таким образом, {F1,F2,F3}~{R, F3,}.                                                                         (3) Но система двух сил находится в равновесии только в том случае, если они направлены вдоль одной прямой. Следовательно, линия действия F3 должна совпасть с линией действия R, т.е. пройти через точку О.

Замечание. Доказанное усло­вие является необходимым, но не достаточным условием равновесия. Для достаточности нужно еще равенство нулю геометрической суммы приложенных сил (см. § 3.4).