5. Равновесие системы сходящихся сил. Теорема о трех силах. Понятие о статической определимости системы сил.

Равновесие системы сходящихся сил.Из законов механики следует, что твердое тело, на которое действуют взаимно уравновешенные внешние силы, может не только находиться в покое, но и совершать движение, которое мы назовем движением «по инерции». Таким движением будет, например, поступательное равномерное и прямолинейное движение тела.Отсюда получаем два важных вывода: 1) Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции». 2) Уравновешенность сил, приложенных к свободному твердому телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела; в покое тело будет при этом находиться лишь в том случае, если оно было в покое и до момента приложения к нему уравновешенных сил. Для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме.

1. Геометрическое условие равновесия. Так как равнодействующая R сходящихся сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил, то R может обратиться в нуль тогда и только тогда, когда конец последней силы в многоугольнике совпадает с началом первой, т. е. когда многоугольник замкнется.

Следовательно, для равновесия системы, сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут.

1. Аналитические условия равновесия. Аналитически равнодействующая системы сходящихся сил определяется формулой

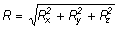
Теорема о трех силах. Если (абсолютно твердое) тело находится в равновесии под действием плоской системы трех непараллельных сил (т.е. сил, из которых хотя бы две непараллельные), то линии их действия пересекаются в одной точке. Доказательство. Пусть из трех сил F1, F2, F₃ , приложенных соответственно в точках А, В и С (рис.3), непараллельными являются F1 и F2. Продолжим линии их действия до пересечения в точке О и перенесем в эту точку обе силы. Очевидно, система {F1, F2} эквивалентна , а эта последняя уже имеет равнодействующую R. Таким образом, {F1,F2,F3}~{R, F3,}.                                                                         (3) Но система двух сил находится в равновесии только в том случае, если они направлены вдоль одной прямой. Следовательно, линия действия F3 должна совпасть с линией действия R, т.е. пройти через точку О.

Замечание. Доказанное усло­вие является необходимым, но не достаточным условием равновесия. Для достаточности нужно еще равенство нулю геометрической суммы приложенных сил (см. § 3.4).