
- •Тема 4.1. Інтерполяція функцій. Інтерполяційний многочлен Лагранжа. -2 год.
- •Поняття про наближення функції
- •Точкова апроксимація
- •Обчислення значень многочлена за схемою Горнера
- •Наближення функцій багаточленами Тейлора
- •Інтерполяційний багаточлен Лагранжа
- •Багаточлени Чебишева
- •Властивості багаточленів Чебишева:
- •Вузли, що мінімізують похибку інтерполяції
- •Порівняння багаточленів Лагранжа та Тейлора
- •Контрольні питання для самоперевірки
- •Завдання
Інтерполяційний багаточлен Лагранжа
Нехай
відомі значення деякої функції
у
![]() -й
різних точках
-й
різних точках
![]() .
Позначимо їх наступним чином:
.
Позначимо їх наступним чином:
![]() ,
,
![]() .
.
Ці значення можуть бути отримані експериментально або знайдені за допомогою обчислень.
Виникає
задача знаходження значення функції у
довільній точці
.
Часто для розв’язання цієї задачі
використовується алгебраїчний багаточлен
![]() ступеню
,
який в точках
,
,
приймає ті ж самі значення, що і функція
ступеню
,
який в точках
,
,
приймає ті ж самі значення, що і функція
![]() :
:
![]() ,
.
,
.
Такий
багаточлен називається інтерполяційним
багаточленом,
а точки
![]() -
вузлами
інтерполяції.
-
вузлами
інтерполяції.
Наближене
обчислення функції
за
формулою
![]() називається
інтерполяцією
функції
за
допомогою алгебраїчного багаточлена
.
Якщо точка, в якій треба знайти значення
функції
,
розташована за межами мінімального
відрізку, що містить всі вузли інтерполяції
,
то заміну функції
називають
екстраполяцією.
називається
інтерполяцією
функції
за
допомогою алгебраїчного багаточлена
.
Якщо точка, в якій треба знайти значення
функції
,
розташована за межами мінімального
відрізку, що містить всі вузли інтерполяції
,
то заміну функції
називають
екстраполяцією.
Теорема. Існує єдиний інтерполяційний багаточлен порядку , що задовольняє умові , .
Доведення: Існування інтерполяційного багаточлена встановимо безпосередньо, записавши його вираз.
Нехай
![]() .
Тоді існує два значення аргументу
.
Тоді існує два значення аргументу
![]() .
Можна записати рівняння прямої, що
проходить через дві точки -
.
Можна записати рівняння прямої, що
проходить через дві точки -
![]() та
та
![]() (рис.
4.1.2):
(рис.
4.1.2):
 .
.
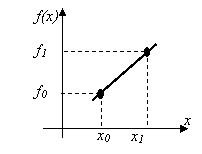
Рис. 4.1.2.
В загальному випадку формула для інтерполяційного багаточлена має вигляд:
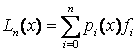 ,
(13)
,
(13)
де
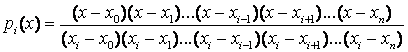 ,
причому очевидно, що
,
причому очевидно, що
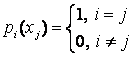 ,
оскільки якщо
,
оскільки якщо
![]() ,
то одна з дужок чисельника
,
то одна з дужок чисельника
![]() обов’язково
дорівнюватиме нулю.
обов’язково
дорівнюватиме нулю.
Багаточлен
називається інтерполяційним
багаточленом Лагранжа,
а функції
![]() -
лагранжевими
коефіцієнтами.
-
лагранжевими
коефіцієнтами.
Доведемо, що - єдиний поліном, що задовольняє умові .
Нехай
існує іншій поліном
![]() ,
такий, що
,
такий, що
![]() .
Тоді багаточлен
.
Тоді багаточлен
![]() дорівнює
нулю у вузлах інтерполяції:
дорівнює
нулю у вузлах інтерполяції:
![]() ,
,
![]() .
Отже, на всьому відрізку
.
Отже, на всьому відрізку
![]()
![]() .
Це означає, що
.
Це означає, що
![]() при
всіх дискретних значеннях
.
Отже,
–
єдиний поліном.
при
всіх дискретних значеннях
.
Отже,
–
єдиний поліном.
Теорему доведено.
Для початкової функції та інтерполяційного багаточлена можна записати рівність:
![]() ,
,
де
![]() -
залишковий член, тобто похибка
інтерполяції, оцінка якої за аналогією
з багаточленом Тейлора проводиться
згідно виразу:
-
залишковий член, тобто похибка
інтерполяції, оцінка якої за аналогією
з багаточленом Тейлора проводиться
згідно виразу:
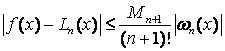 ,
,
де
![]() ,
-
вузли інтерполяції,
,
-
вузли інтерполяції,
![]() .
.
Максимальна похибка інтерполяції:
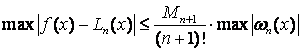 .
.
Багаточлени Чебишева
Якщо задана деяка функція на відрізку , то виникає питання: як обрати вузли інтерполяції так, щоб похибка наближення функції інтерполяційним багаточленом була мінімальною.
Розв’язок
може бути знайдений для різноманітних
часткових випадків функції
.
Але мінімізувати величину
![]() ,
що входить у праву частину виразу (14)
оцінки похибки, можна за допомогою
використання поліномів Чебишева.
,
що входить у праву частину виразу (14)
оцінки похибки, можна за допомогою
використання поліномів Чебишева.
Для
простоти розглянемо відрізок зміни
аргументу
![]() .
Багаточлен Чебишева
.
Багаточлен Чебишева
![]() ,
,
![]() на
відрізку
на
відрізку
![]() задається
формулою:
задається
формулою:
![]() .
.
Зокрема,
при
![]()
![]() ,
при
,
при
![]() .
.
Розглянемо тригонометричні формули:
![]() ,
,
![]() ,
,
![]() .
.
Покладемо
![]() .
Тоді можна записати вираз для полінома
Чебишева:
.
Тоді можна записати вираз для полінома
Чебишева:
![]() ,
,
![]() .
.
![]() ,
,
або
![]() .
.
Ми
отримали рекурентну формулу для поліномів
Чебишева. Знаючи, що
![]() ,
,
![]() і
поширюючи рекурентну формулу на всю
вісь
,
знайдемо:
і
поширюючи рекурентну формулу на всю
вісь
,
знайдемо:
:
![]() .
.
![]() :
:
![]() .
.
![]() :
: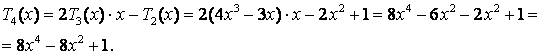
і т.д.
Властивості багаточленів Чебишева:
Властивість 1. При парному (непарному) багаточлен містить лише парні (непарні) степені , тобто є парною (непарною) функцією.
Властивість
2.
Старший коефіцієнт багаточлена
при
![]() дорівнює
дорівнює
![]() .
.
Властивість 3. Багаточлен має дійсних коренів на відрізку , які виражаються формулою:
![]() .
.
Дійсно,
![]() .
.
Властивість
4.
![]() ,
причому
,
причому
![]() ,
де
,
де
![]() ,
,
![]() .
.
Дійсно,
![]() ,
,
![]() ,
.
,
.
Властивість
5.
Багаточлен
![]() ,
серед всіх багаточленів
-го
степеня зі старшим коефіцієнтом, що
дорівнює одиниці, має на відрізку
найменше
значення максимума модуля, тобто не
існує такого багаточлена
,
серед всіх багаточленів
-го
степеня зі старшим коефіцієнтом, що
дорівнює одиниці, має на відрізку
найменше
значення максимума модуля, тобто не
існує такого багаточлена
![]() -го
степеня зі старшим коефіцієнтом, що
дорівнює одиниці, щоб
-го
степеня зі старшим коефіцієнтом, що
дорівнює одиниці, щоб
![]() .
.
Завдяки властивості 5 багаточлени Чебишева називають багаточленами, що найменше відхиляються від нуля.
