Тема 4.1. Інтерполяція функцій. Інтерполяційний многочлен Лагранжа. -2 год.
[1] Гл.4. п.4.3 С.197-199
Поняття про наближення функції
На практиці часто зустрічаються задачі, які вимагають наближення (апроксимації) функції:
1. Прискорення часу обчислення функції.
Припустимо,
що розв’язання деякої задачі пов’язане
з багатократним обчисленням функції,
заданої громіздким виразом. Тоді природно
буде замінити
близькою
більш простою функцією
з
меншим часом обчислення, щоб виконувалося
співвідношення:
,
де
–
точність апроксимації.
2. Економія пам’яті ЕОМ.
Припустімо,
що функція
задана
своїми значеннями в точках
,
де
,
на інтервалі
:
|
|
... |
|
|
|
... |
|
При
великому числі
зберігання
всієї таблиці в пам’яті ЕОМ може
виявитися взагалі неможливим. Тоді
постає задача апроксимації точкової
функції
близькою
їй функцією, що залежить від невеликої
кількості параметрів
.
При цьому в пам’яті зберігаються
значення цих параметрів, а значення
функції
обчислюються
наближено.
3. Пошук закономірностей за експериментальними даними.
Результати
експериментів зазвичай представляють
у вигляді таблиці. Експериментатор
припускає, що отримана залежність
(результати) є реалізацією емпіричного
закону з невідомим параметром
.
Тоді виникає задача визначення
та
,
які найкращим чином апроксимують
експериментальні дані.
Апроксимацією називають знаходження такої функції, яка найточніше (з точністю до ) описує функцію, задану у вигляді таблиці.
Точкова апроксимація
Одним з основних типів точкової апроксимації є інтерполяція.
Найпростіша
задача інтерполяції полягає в наступному:
на відрізку
задані
точок
,
які називаються вузлами
інтерполяції,
і значення деякої функції у цих точках:
.
Необхідно
побудувати функцію
(інтерполяційну
функцію), яка приймає у вузлах інтерполяції
ті самі значення, що й функція
.
Тобто треба знайти таку
,
щоб
.
Геометрично
це означає, що треба знайти криву
певного
типу, що проходить через задану систему
точок
,
(рис.
4):
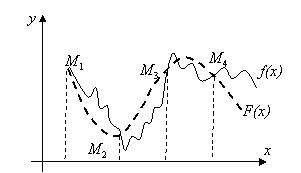
Рис. 4.1.1
В такій постановці задача інтерполяції має нескінченну кількість розв`язків.
Раніше
під інтерполяцією розуміли відшукування
значень функції у проміжних точках між
вузлами інтерполяції (наприклад,
),
значення яких відсутні у таблиці, тобто
“мистецтво читання між рядками”. В
більш широкому розумінні інтерполяція
? це процес обчислювання функції, яка
проходить крізь задані точки (вузли
інтерполяції). Теоретично, по цих точках
можливо побудувати багато функцій.
Основна
мета інтерполяції – знайти швидкий
(економічний) алгоритм обчислення
функції
для
значень
,
які не містяться у таблиці.
Обчислення значень многочлена за схемою Горнера
Розглянемо алгебраїчний многочлен
,
де
– числові коефіцієнти
– степінь многочлена. Обчислити значення
многочлена при фіксованому значенні
можна декількома способами:
за допомогою багатократного множення знайти степені
,
,
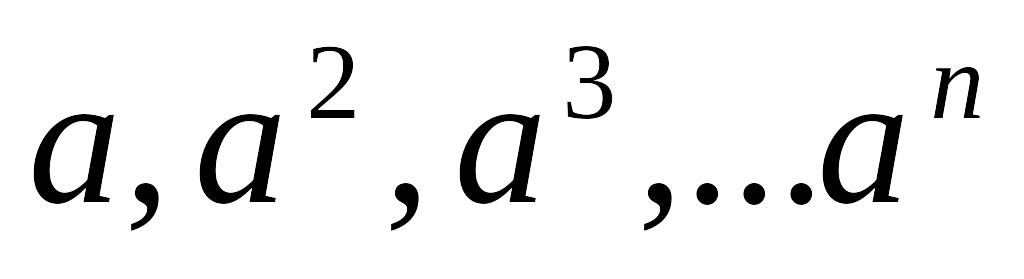потім виконати ще
множень степенів на коефіцієнти і
додавань. Цей, на перший погляд
найпростіший спосіб, вимагає виконання
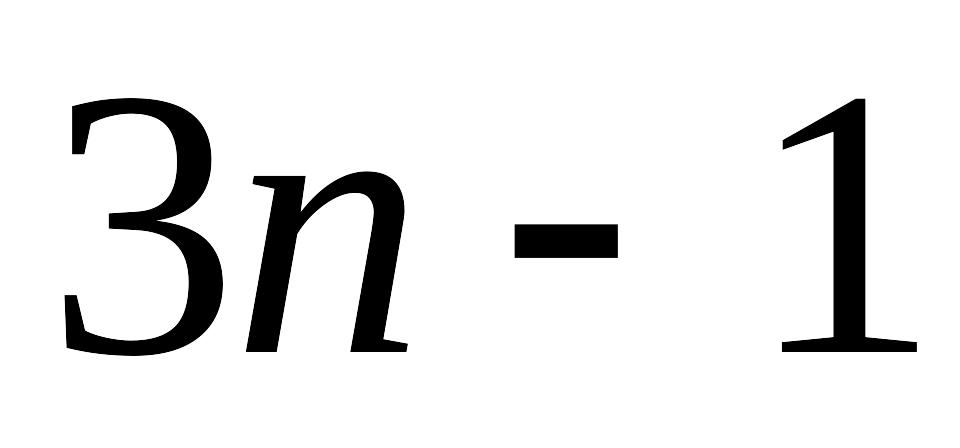арифметичних дій.Більш економічно можна обчислити значення многочлена в заданій точці, якщо його переписати у наступному вигляді:
.
Тоді обчислення значення полінома зведеться до послідовного обчислення наступних значень:
,
...
Такий
спосіб обчислення значення полінома
називається схемою Горнера. За цією
схемою для обчислення значення необхідно
виконати лише
множень і
додавань (
операції). В ручну обчислити значення
многочлена за схемою Горнера можна за
допомогою таблиці наступним чином:
|
|
|
|
... |
|
+ |
|
|
|
... |
|
|
|
|
|
... |
|
Приклад. Обчислити
при
|
-1 |
2 |
-1 |
3 |
-4 |
1 |
+ |
|
1,5 |
-5,25 |
9,375 |
-18,5625 |
33,84375 |
|
-1 |
3,5 |
-6,25 |
12,375 |
-22,5625 |
34,84375= |
Якщо многочлен є парною функцією, то його зручно представляти як
якщо – непарна, то
Необхідно зауважити, що при обчисленні значень многочленів з великими коефіцієнтами за допомогою комп‘ютера може виникнути значна втрата точності. Цього можна уникнути за рахунок використання рекурентних формул.