№ 1

Методические указания и контрольные задания

по курсу «Математика. Спецглавы.(линейная алгебра и комплексные числа)»

для студентов заочного факультета

по направлениям 210700, 220700, 230400

Санкт -Петербург

ГУТ

2012

Методические указания и контрольные задания по курсу математики для студентов заочного факультета по направлениям 210700, 220700, 230400. № 5.

Сост. Г. М. Полевая, И.С. Перфилова, Г.И. Рудинская, Е. Я. Раковщик. ГУТ СПб, 2012.

Методические указания содержат варианты контрольных работ по линейной алгебре и комплексным числам для студентов заочного отделения, а также указания по их выполнению и упражнения для самопроверки.

Комплексные числа

1. Определение комплексного числа, его геометрический смысл. Тригонометрическая и показательная формы комплексного числа.

2. Алгебраические действия над комплексными числами в алгебраической, тригонометрической и показательной формах.

3. Возведение в степень комплексного числа.

4. Извлечение корня n-й степени из комплексного числа.

Линейная алгебра

1. Матрицы. Различные виды матриц. Действия над матрицами.

2. Формулировка свойств определителей второго и третьего порядка.

3. Миноры и алгебраические дополнения. Теоремы разложения, замещения, аннулирования.

4. Определение обратной матрицы и её нахождение.

5. Системы трёх линейных уравнений с тремя неизвестными. Теорема Крамера.

Векторная алгебра и аналитическая геометрия

1. Скалярное произведение векторов, его свойства.

2. Выражение скалярного произведения через координаты перемножаемых векторов.

3. Векторное произведение векторов, его свойства.

4. Выражение векторного произведения через координаты перемножаемых векторов.

6. Смешанное (векторно-скалярное) произведение векторов, его геометрический смысл.

7. Выражение смешанного произведения через координаты перемножаемых векторов.

8. Компланарные вектора. Необходимое и достаточное условия компланарности трёх векторов.

9. Уравнения прямой в пространстве.

10. Вычисление угла между двумя прямыми в пространстве. Условия параллельности и перпендикулярности двух прямых в пространстве.

11. Уравнение плоскости.

12. Определение угла между прямой и плоскостью, его вычисление. Условие параллельности и перпендикулярности прямой и плоскости.

13. Определение эллипса, его каноническое уравнение.

14. Определение гиперболы, её каноническое уравнение.

15. Определение параболы. Вывод канонического уравнения параболы.

Комплексные числа

Комплексным числом z называется выражение вида x+iy, где x и y – вещественные числа; xназывается вещественной частью комплексного числа, y – мнимой частью, а i – мнимой единицей. По определению полагают i²=-1. Приняты обозначения – для вещественной части x=Rez, для мнимой части y=Imz. Обратите внимание, что мнимой частью комплексного числа является y, не iy! Если y=0, то число z является вещественным.

Комплексные числа z₁ и z₂ называются равными. Если Rez₁=Rez₂ и Imz₁=Imz₂. Если z=x+iy, то число называется сопряженным с числом z. Для комплексных чисел определены операции сложения и вычитания, умножения и деления, возведения в степень и извлечения корня и т.д. Напомним сначала определение первых четырёх операций:

;

;

;

если .

Отсюда видно, что умножение чисел состоит в перемножении двучленов, замене i² числом -1 и приведении подобных членов; деление состоит в умножении делимого и делителя на число, сопряженное делителю, и почленного деления вещественной и мнимой частей нового делимого на новый делитель.

Примеры.

1. Найти мнимую часть числа .

Поскольку , то Imz=-4.

2. Вычислить .

.

3. При каких вещественных x и y справедливо равенство?

?

Сначала преобразуем левую часть:

Следовательно, . Отсюда:

т.е. x=-8, y=-1.

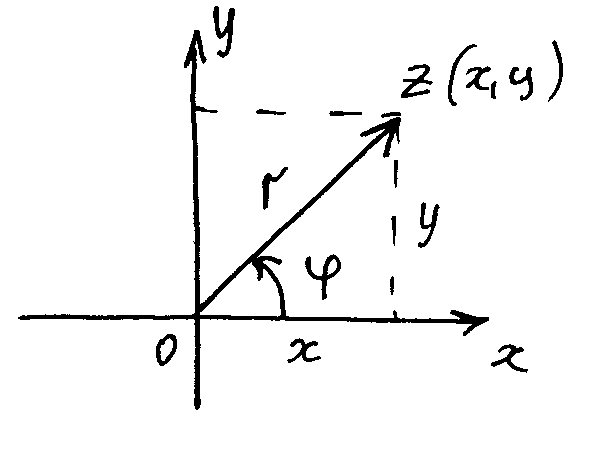Комплексное число z=x+iy изображается вектором на плоскости с началом в точке (0,0) и концом в точке (x,y). Из чертежа видно, что , где и - угол между положительным направлением оси Ox и вектором. Отсюда . Число r называется модулем комплексного числа z и обозначается через ; число называется аргументом числа z и обозначается через argz. Известно, что имеет место формула Эйлера . Поэтому

.

называется алгебраической формой комплексного числа;

называется тригонометрической формой комплексного числа;

называется показательной формой комплексного числа.

Функция обладает всеми свойствами степи, т.е.

Кроме того, при к=0, 1, 2,…,n. Обратите внимание, что корень степени n имеет в комплексной области ровно n различных значений.

Итак, , где , . Переход от алгебраической формы к показательной и тригонометрической формам комплексного числа надо осуществлять по схеме, описанной ниже.

Обязательно изобразить число z=x+iyна комплексной плоскости. Найти φ по чертежу или по чертежу и формуле . Найти .

Примеры.

4. Представить комплексные числа , в показательной и тригонометрической формах.Ясно, что ; вектор лежит в третьей четверти и , так что . Следовательно, . Это и есть показательная форма числа . Далее . Это тригонометрическая форма числа . По определению ; из чертежа видно, что . Следовательно, .

5. Записать: а) число в алгебраической форме,

б) число –i в показательной форме.

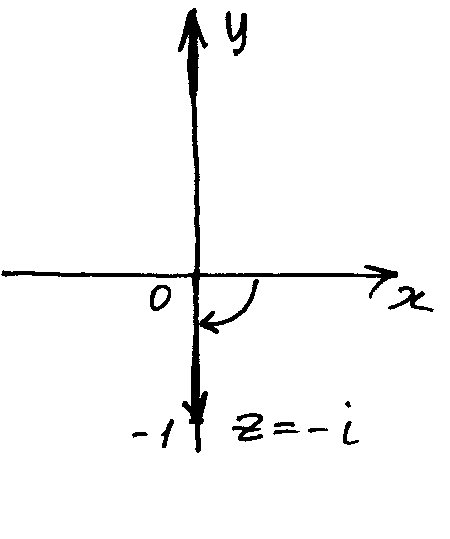
Переход от показательной к алгебраической форме осуществляется через тригонометрическую форму комплексного числа. Таким образом, . Изобразим число на чертеже. По определению ; из чертежа видно, что . Следовательно, .

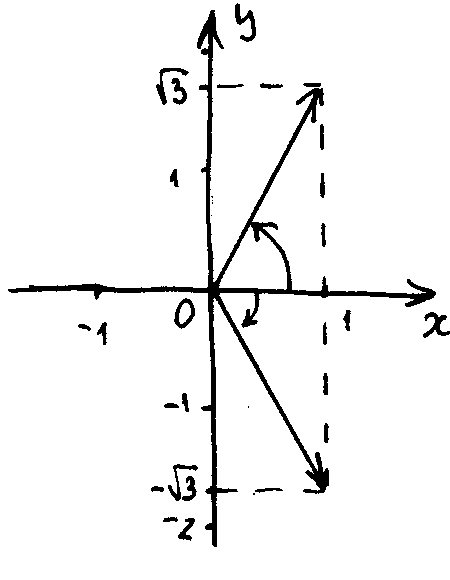
6. Найти комплексное число , сопряженное с . В алгебраической форме . В показательной форме, согласно примеру 4, имеем , из чертежа видно, что . В тригонометрической форме .

.

7. Найти произведение чисел , . Сначала представим числа в показательной форме. Ясно, что , так что . Далее, . Наконец, представим полученное число в алгебраической форме .

8. Вычислить .

Сначала представим число в показательной форме: . Затем вычислим

(Мы воспользовались 2π – периодичностью синуса и косинуса).

9. Решить уравнение

Имеем . Представим число в показательной форме . Тогда , где к=0, 1, 2.

Линейная алгебра

Матрицы

Прямоугольная таблица чисел, состоящая из m строк и n столбцов, называется матрицей строения mxn; при m=n она называется также квадратной матрицей порядка n. Матрицы одинакового строения называются равными, если они равны поэлементно, т.е. для любых ί, j элементы матриц, стоящие в пересечении ί-ой строки и j-го столбца, равны между собой. Для матриц определены следующие операции: умножение матрицы на число; сложение матриц (только одинакового строения); умножение матриц (только в случае, когда число столбцов первого сомножителя равно числу строк второго сомножителя!). Именно

λ ,

где

(сумма произведений элементов ί-ой строки первой матрицы на соответствующие элементы j-го столбца второй матрицы). Заметим, что число строк матрицы-произведения равно числу строк первого сомножителя, а число столбцов – числу столбцов второго. Обратите внимание, что при перемножении матриц сомножители менять местами нельзя, вообще говоря. Поэтому надо следить за порядком множителей (см. пример 10).

Примеры: 10

; не определено!

.