3. Термодинамика открытых систем

1.4.1.Уравнение первого закона термодинамики для открытых систем

Движущееся по каналу рабочее тело образует поток, который представляет собой открытую термодинамическую систему.

Одномерный поток – поток рабочего тела, в котором термодинамические параметры в поперечном сечении имеют постоянное значение, зависящее только от одной координаты, которая определяет положение поперечного сечения в канале.

Стационарный поток – поток, в котором термодинамические параметры в любом сечении потока не зависят от времени. В стационарном потоке выполняется условие неразрывности потока, заключающееся в постоянстве массового расхода рабочего тела в любом сечении:

, (5.1)

где массовый расход рабочего тела (кг/с),

объемный расход рабочего тела (м³/с),

площадь поперечного сечения канала (м²),

линейная скорость потока рабочего тела (м/с),

удельный объем рабочего тела (м³/кг).

Процессы преобразования энергии в потоке рабочего тела широко используются в технике.

Получим уравнение 1-го закона термодинамики для потока газа при следующих допущениях:

- движение газа по каналу установившееся и неразрывное;

- скорости по сечению, перпендикулярному оси канала, постоянны;

- пренебрегается трение частичек газа друг другу и о стенки канала;

- изменение параметров по сечению канала мало по сравнению их абсолютными значениями

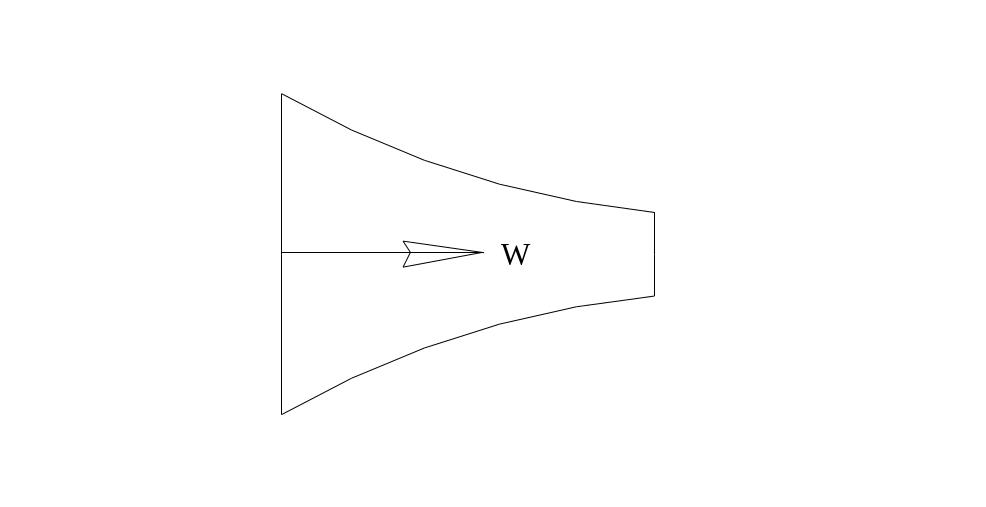
Рассмотрим тепломеханический агрегат, в который поступает рабочее тело с параметрами , , со скоростью . Каждый килограмм рабочего тела может в общем случае получать от внешнего источника (через стенку канала) теплоту и совершать техническую работу , которая отбирается из потока с помощью каких-либо технических устройств.

После этого рабочее тело покидает агрегат с параметрами , , со скоростью . Высота входного и выходного сечений от уровня горизонта составляет соответственно и (м).

К каждому элементарному объему рабочего тела можно применить первый закон термодинамики для закрытых систем в виде:

. (5.2)

Работа расширения рабочего тела в потоке расходуется в следующих направлениях:

а) совершение технической работы при взаимодействии с подвижными стенками агрегата, например, с лопатками рабочего колеса турбины,

б) совершение работы проталкивания рабочего тела от входного сечения к выходному , (5.3)

в) изменение кинетической энергии, равное для 1 кг рабочего тела:

, (5.4)

г) изменение потенциальной энергии, равное для 1 кг рабочего тела:

, (5.5)

д) преодоление сил трения рабочего тела о стенки канала: .

Окончательно:

(5.6)

Работа трения превращается в эквивалентное количество теплоты , которое передается потоку рабочего тела вместе с подведенной теплотой извне. Поэтому общее количество подведенного тепла составляет:

(5.7)

Подставляя (5.3) – (5.7) в (5.2), имеем:

.

Учитывая, что , получаем:

(5.8)

Взятые в скобки слагаемые можно исключить из этого уравнения. Уравнение (5.8) является выражением первого закона термодинамики для потока рабочего тела.

Теплота, подводимая извне к потоку рабочего тела, расходуется на изменение энтальпии рабочего тела, совершение технической работы и изменение кинетической и потенциальной энергии потока.

В дифференциальной форме уравнение (5.8) имеет вид:

(5.9)

Cравнивая это уравнение с уравнением , получаем:

, (5.10)

или в интегральной форме:

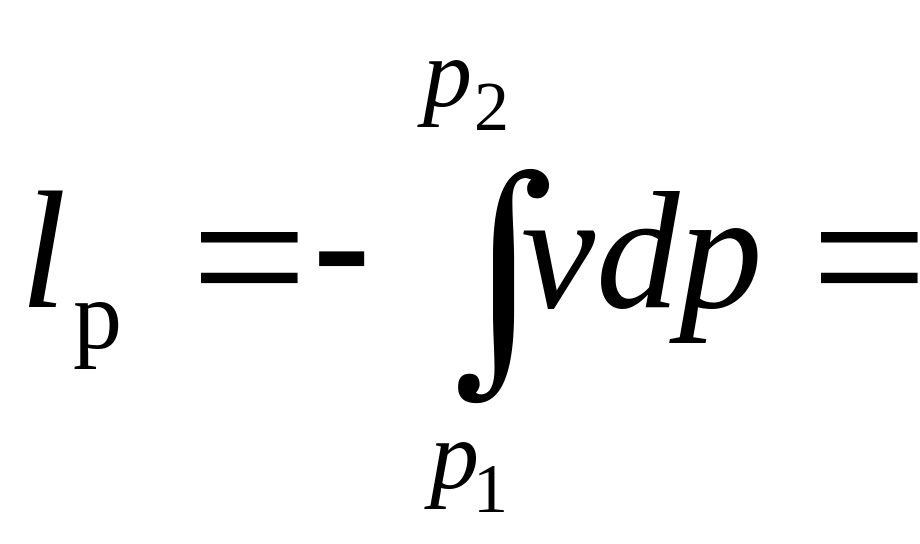
. (5.11)

Здесь - располагаемая работа. В соответствии с (5.11) располагаемая работа – это та часть работы расширения, которая может быть превращена в техническую работу или в кинетическую и потенциальную энергию потока (за вычетом потерь на трение).

Интегрируя выражение , получим:

. (5.12)

Таким образом, располагаемая работа – это работа расширения за выче- том работы проталкивания. Геометрически располагаемая работа выражается площадью между кривой процесса в координатах и вертикальной осью давлений.

Сопловой канал – устройство для увеличения кинетической энергии потока. В сопловых каналах скорости истечения газа или жидкости велики, а длина канала мала. В таких устройствах теплообмен с окружающей средой практически отсутствует, а процесс истечения считается адиабатным (q=0). Технической работы в сопловых каналах не производится =0. Первый закон термодинамики для обратимого адиабатного процесса истечения вещества в сопловом канале будет иметь вид

_.

Уравнение обращения воздействий. Сопла и диффузоры

Изменения условий течения газа, вызывающие соответствующие изменения параметров состояния потока, называются воздействиями. Существует пять видов воздействий:

1. Геометрическое воздействие изменение величины проходного сечения канала вдоль потока.

2. Расходное воздействие — изменение массового расхода газа в канале путем вдува (отсоса) дополнительной массы через боковую поверхность.

3. Механическое воздействие — обмен механической энергией в форме технической работы между потоком газа и окружающей средой.

4. Тепловое воздействие — подвод (отвод) тепла в поток.

5. Воздействие трением — учет влияния реально существующих сил вязкого трения в рамках модели идеального газа.

Течение газа описывается следующими уравнениями:

1. уравнение непрерывности G = сF ;

2. уравнение энергии (уравнение 1-го закона термодинамики):

;

3. уравнение движения (Бернулли):

;

4. уравнение состояния идеального газа p=RT;

5. число Маха М=с/а.

Проведя термодинамический анализ влияния перечисленных факторов на характеристики газового потока, Л.А. Вулис получил уравнение, которое получило название уравнение обращения воздействия.

.

Особенность этого выражения заключается в том, что знак его левой части изменяется при переходе значения скорости через критическое (M=1), поэтому характер влияния отдельных физических воздействий на газовое течение противоположен при дозвуковом и сверхзвуковом режимах. Воздействия, вызывающие ускорение (dc > 0 в дозвуковом по токе (M < 1) — сужение капала dF<0, подвод дополнительной массы газа dG > 0, совершение газом работы dl_техн > 0, трение dq_тр>0 приводят к замедлению сверхзвукового потока; воздействия обратного знака (dF > 0; dG < 0; dl_техн < 0; dl_тр; dq < 0), приводят к замедлению дозвукового потока и ускорению сверхзвукового. Отсюда следует важный вывод: под влиянием одностороннего воздействия величину скорости газового потока можно довести до критической, но нельзя перевести через нее.

Сопла и диффузоры

Рассмотрим воздействие формы канала dF на адиабатное течение в соплах и диффузорах. Сопла – это каналы, в которых происходит расширение газа и увеличение скорости его движения. В диффузорах происходит сжатие газа и уменьшение скорости его движения.

В формулировках сопел и диффузоров не оговаривается возможная геометрия этих каналов. Это не случайно, так как их продольный профиль зависит от условий течения газа.

Для геометрического воздействия уравнение Вулиса запишется в виде:

Анализ уравнения показывает, что когда скорость газа на входе в канал меньше местной (то есть в данном сечении канала) скорости звука ( <0), сопло должно быть суживающимся, а диффузор - расширяющимся; если скорость потока во входном сечении канала превышает местную скорость звука ( >0), то сопло должно быть расширяющимся, а диффузор суживающимся.

Канал	Знак	Знак	Знак	Форма канала
Сопло	<0	<0	>0
	>0	>0	>0
Диффузор	<0	>0	<0
	>0	<0	<0

Параметры торможения

Для адиабатического течения на участке 1-2 уравнение энергии имеет вид:

,

где h* - полная энтальпия, или энтальпия адиабатно заторможенного потока (при скорости потока с=0). Таким образом, при движении газа его полная энергия, состоящая из кинетической энергии видимого движения и энергии, выражаемой энтальпией h=u+pv, остается постоянной. Всякое изменение кинетической энергии вызывает соответствующее изменение его энтальпии, а, следовательно, и температуры. В соплах скорость увеличивается, а температура уменьшается. В диффузорах скорость уменьшается, а температура увеличивается.

При полном торможении потока (с=0) температура принимает наибольшее значение и называется температурой полного торможения Т*. Для идеального газа с_р=const, h=c_pT тогда полная энтальпия (энтальпия заторможенного потока) h*=c_pT*. Уравнение энергии можно записать в виде:

c_pT*=c_pT+ , или ,

где Т – статическая температура (температура движущейся среды.

Преобразуем уравнение к следующему виду:

,

M=с/a – число Маха; a²=кRT; а – скорость звука.

Тогда окончательно получим выражение для расчета скорости торможения:

.

Расчет давления торможения проводится по формуле:

.

Плотность заторможенного потока будет равна:

.

Приведенные параметры

Для расчета параметров можно использовать таблицы газодинамических функций, которые облегчают решение задач. При этом вводится приведенная скорость , где критическая скорость , а .

Тогда получим:

Приведенная температура – отношение действительной температуры потока к температуре торможения:

.

Приведенное давление – отношение действительного давления в сечении (статического давления) к давлению торможения:

.

Приведенная плотность – отношение действительной плотности газа к плотности заторможенного потока:

.

Приведенная плотность потока массы – отношение плотности потока массы в данном сечении к плотности потока массы в критическом сечении:

.

Располагая таблицами, в которых для каждого значения или М указаны значения функций , q можно быстро переходить от действительных (термодинамических) параметров потока к параметрам торможения и обратно.

Истечение газа из суживающегося сопла

При изучении этого процесса предполагается, что истечение происходит при постоянных параметрах газа на входе в сопло и на выходе из него.

Пусть давление cреды, откуда происходит истечение, равно , а давление той cреды, куда вытекает газ (так называемое противодавление), равно . Пусть начальные параметры газа (на входе в сопло) известны и равны .

С корость газа на выходе из сопла можно определить, используя формулу

откуда

если выходная скорость значительно больше скорости газа на входе ( ), т.е. , получим

.

Для идеального газа с_р=const, h=c_pT, полная энтальпия h*=c_pT*, , тогда скорость потока на выходе из сопла:

.

Обозначим отношение давлений , то получим

.

Для определения массового расхода газа используется уравнение сплошности применительно к выходному сечению площадью :

.

Таким образом, секундный расход газа G зависит от площади выходного сечения сопла F₂, начального состояния газа на входе в сопло (p₁, ₁, T₁) и степени расширения газа (от отношения давления на выходе из сопла к давлению газа на входе в сопло р₂/р₁^*).

На основании формул и экспериментальных исследований построены графические зависимости скорости и массового расхода газа в суживающемся сопле от перепада давления .

При =1, когда давление до и после сопла одинаково, движение потока отсутствует, скорость и массовый расход газа равны нулю.

По мере уменьшения  скорость потока в выходном сечении возрастает, и при  = 0, что соответствует истечению в вакуум, она достигает максимума:

где ab0 – теоретическая зависимость; abc – действительная зависимость, полученная опытным путем; I – подкритическая область истечения (дозвуковая): ; III – надкритическая область истечения (сверхзвуковая): .

В точке «b» скорость истечения газа равна местной скорости звука с=a, и скорость распространения возмущений вверх по потоку , т.е. волны возмущений не проходят вверх по потоку от среза сопла при дальнейшем уменьшении величины .

Таким образом в зависимости от отношения давлений можно выделить три характерных режима истечения газа: при − докритический, при − критический и при − сверхкритический режимы.

При равном расход газа достигает максимума и находится по формуле:

При докритическом режиме истечения в сопле происходит полное расширение газа с понижением давления от до , на срезе сопла , скорость на выходе меньше скорости звука (рис. а), располагаемая работа, соответствующая площади 1'-1-2-2'-1', полностью расходуется на увеличение кинетической энергии газа. При критическом режиме также происходит полное расширение газа в пределах сопла, на срезе сопла , скорость на выходе равна критической скорости – скорости звука (рис. б), располагаемая работа полностью расходуется на увеличение кинетической энергии газа. При сверхкритическом режиме в пределах сопла происходит неполное расширение газа, давление понижается только до критического, на срезе сопла , скорость на выходе равна критической скорости – местной скорости звука (рис. в). Дальнейшее расширение газа и понижение его давления до осуществляется за пределами сопла. На увеличение кинетической энергии расходуется только часть располагаемой работы, соответствующая площади 1'-1-2-2'-1', другая ее часть, соответствующая площади 2'-2-2₀ –2₀'-2', в суживающемся сопле остается не реализуемой.

.

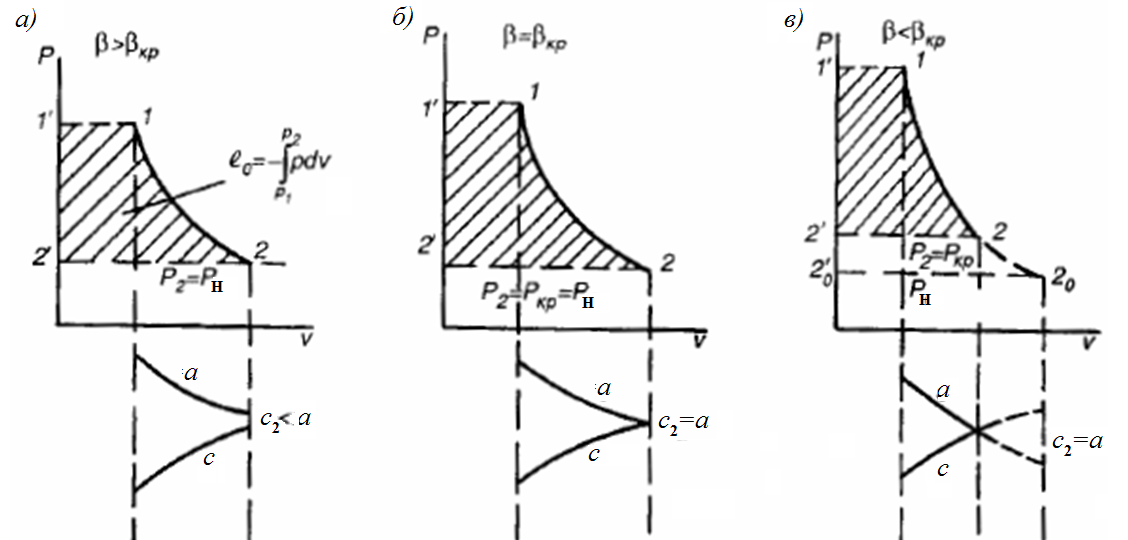
Рис. Процесс истечения газа в pv – координатах и характер изменения скорости звука и скорости истечения газа

а – при ; б – при ; в – при

Режимы работы суживающегося сопла

I режим – режим полного расширения , когда ,

Скорость газа на выходе из суживающегося сопла определяется по формуле:

.

Mассовый расход газа:

.

I I режим – режим полного расширения, когда , .

Скорость газа на выходе из суживающегося сопла равна критической скорости и определяется по формуле:

.

Mассовый расход газа:

.

I I I режим – режим недорасширения, когда , ,

.

Скорость газа на выходе из суживающегося сопла равна критической скорости и определяется по формуле:

.

Mассовый расход газа:

.

Истечение газа из сопла Лаваля.

Комбинированное сопло Лаваля предназначено для использования больших перепадов давления и для получения скоростей истечения, превышающих критическую скорость (скорость звука). Условием закритического процесса истечения рабочего тела служит p_Н/p₁ <β_кр . В сопле Лаваля выделяют три основные области.

1. Суживающаяся короткая часть, в которой скорость потока дозвуковая.

2. Узкое сечение, в котором газ движется со скоростью звука.

3. Расширяющаяся конусообразная насадка (сверхзвуковая скорость потока).

Главным условием выбора размеров широкой части сопла Лаваля для истечения рабочего тела является безотрывность его от стенок насадки. Поэтому угол раствора конуса должен быть 8-12^o, это помогает устранить существенные потери вследствие расширения газа. При больших углах наблюдается отрыв струи от стенок канала.

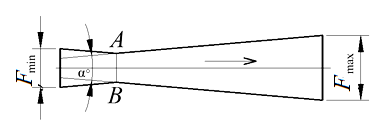
Рис. Сопло Лаваля

Рассмотрим процессы, происходящие при работе комбинированного сопла. В том случае, когда давление внешней среды p_Н < p_кр,скорость и давление потока в узком сечении сопел являются критическими.

Конструкция сопла Лаваля позволяет для каждого отношения 0< p_Н/p₁ < 1 получить полное расширение. При этом в выходном сечении сопла энергия не теряется, а при выравнивании давления рабочего тела и внешней среды скорость потока становится сверхзвуковой, что необходимо для применения сопла на практике. В таком случае массовый расход становится максимальным, его величина зависит от площади наименьшего сечения сопла (F_min).

В узкой части сопла (называемой горлом) устанавливаются критические значения параметров ρ_кр, Т_кр, p_кр, с_кр= а, G_max (где а– местная скорость звука). Движение потока по расширяющейся части характеризуется тем, что газ расширяется далее, повышается скорость от с_кр= а до с₂ > а, что ведет к уменьшению давления.

Расширяющаяся часть насадки может выполнять функцию диффузора, если в горле сопла  с < а (для p_Н/p₁ > β_кр ).

Скорость газа на выходе из сопла Лаваля определяется по формуле:

Скорость в минимальном сечении сопла:

.

Mассовый расход газа:

.

Максимальная скорость истечения

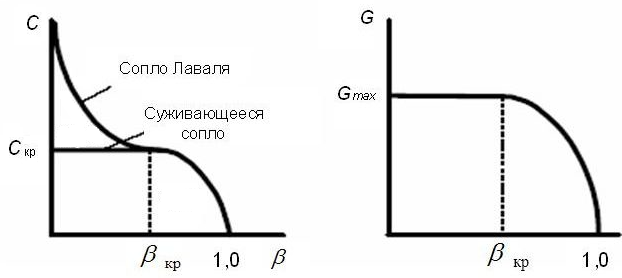
Рис. Изменение скорости истечения и расхода газа через суживающееся сопло и сопло Лаваля от отношения давлений

Площадь минимального сечения сопла определяется по формуле

.

Площадь выходного сечения сопла

.

Длина расширяющейся части сопла определяется по уравнению

,

где d₂ и d_min – соответственно диаметры выходного и минимального сечений, α– угол конусности расширяющейся части.

 Истечение газов с учетом трения

Выведенные выше формулы скорости истечения и массового расхода газа справедливы только для обратимого процесса истечения, так как не учитывают силы трения рабочего тела о стенки канала и внутреннее трение между струйками потока из-за различия скоростей по сечению канала.

В отличие от теоретического изоэнтропийного действительный процесс истечения реального газа происходит при трении частиц газа между собой и о стенки канала. При этом работа, затрачиваемая на преодоление сил трения, преобразуется в теплоту, в результате чего температура и энтальпия газа в выходном сечении канала возрастают. Истечение газа с трением становится необратимым процессом и сопровождается увеличением энтропии. На рис. в sh — координатах представлены процессы расширения газа 1—2 при истечении без трения и 1-2_д при истечении с трением. При одинаковом перепаде давлений р₁ − р₂ действительный теплоперепад ∆h_д = h₁-h_2д меньше располагаемого ∆h = h₁ − h₂. В результате этого действительная скорость истечения газа оказывается меньше теоретической.

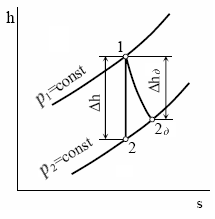
Рис. Изоэнтропийный и действительный процессы истечения газа

в sh – диаграмме

Отношение разности располагаемого и действительного теплоперепадов (потери теплоперепада) к располагаемому теплоперепаду называется коэффициентом потери энергии

ζ_с = (∆h − ∆h_д)/∆h.

Отсюда

∆h_д = (1 − ζ_с)·∆h.

Коэффициентом потери скорости называется отношение действительной скорости истечения к теоретической

.

Коэффициент потери скорости, учитывающий уменьшение действительной скорости по сравнению с теоретической, в современных соплах равен 0,95 — 0,98.

Отношение действительного теплоперепада ∆h_д к теоретическому ∆h, или действительной кинетической энергии к теоретической называется коэффициентом полезного действия канала

.

или

.