2. Теплоемкость газов

Под теплоемкостью газа (удельной теплоемкостью) понимают количество тепла, необходимое для нагревания количественной единицы газа (1 кг, 1м³, 1 киломоль) на 1⁰С (или 1 К). В соответствии с этим различают теплоемкость массовую, объемную и мольную.

, (1.35)

где удельная массовая теплоемкость (Дж/кг^.К, кДж/кг^.К),

удельная объемная теплоемкость (Дж/м^3.К, кДж/м^3.К),

мольная теплоемкость (Дж/кмоль^.К, кДж/кмоль^.К).

При этом имеют место соотношения:

. (1.36)

Величина теплоемкости зависит от рода газа, его температуры, давления и условий нагрева газа.

Теплоемкость газовой смеси определяется через теплоемкости компонентов:

(1.37)

Теплоемкость, как и теплота процесса, зависит от характера процесса, что обозначается индексом процесса например:

Чаще всего используется теплоемкость при постоянном объеме - и теплоемкость при постоянном давлении - .

(1.38)

Из (1.26) при получаем а из (1.29) при получаем . Отсюда:

. (1.39)

. (1.40)

Для идеального газа изобарная и изохорная теплоемкости связаны между собой уравнением Майера:

. (1.41)

Отношение изобарной теплоемкости и изохорной:

. (1.42)

В классической теории теплоемкости теплоемкость идеальных газов не зависит от температуры и определяется числом степеней свободы поступа-тельного и вращательного движения молекул газа - .

, , (1.43)

Для одноатомных газов для двухатомных , для трехатомных

Однако теплоемкость реальных газов зависит от температуры, что объясняет квантовая теория теплоемкости, учитывающая колебательные степени свободы. Поэтому наряду с истинной теплоемкостью, определяемой по (1.35), вводится средняя теплоемкость в интервале температур от до :

. (1.44)

Значения истинной теплоемкости при заданной температуре (^оС) и средней теплоемкости в интервале температур от 0(^оС) до (^оС) приводятся для различных газов в справочных таблицах.

Количество теплоты, необходимой для нагревания газа от температуры до температуры , определяется по формуле:

(1.45)

1.2. Термодинамические процессы идеального газа

Задачей исследования термодинамических процессов является нахождение зависимостей и величин, характеризующих эти процессы:

1. уравнений, описывающих процесс;

2. аналитической взаимосвязи между параметрами рассматриваемого процесса, т.е. связи между параметрами p, v, T;

3. величины изменения внутренней энергии за процесс;

4. величины изменения энтальпии рабочего тела за процесс;

5. величины работы изменения объема рабочего тела и располагаемой работы;

6. количества тепла, подведенного за время процесса к рабочему телу или отведенного от него.

Изохорный процесс – процесс, протекающий при постоянном объеме.

n=

Уравнение, связывающее параметры начального и конечного состояний:

. (2.1)

Работа процесса:

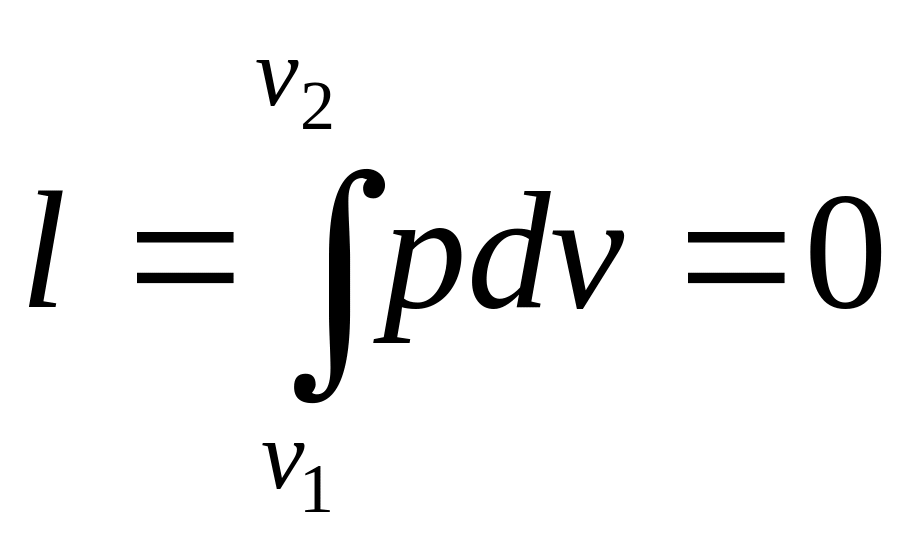. (2.2)

Располагаемая работа:

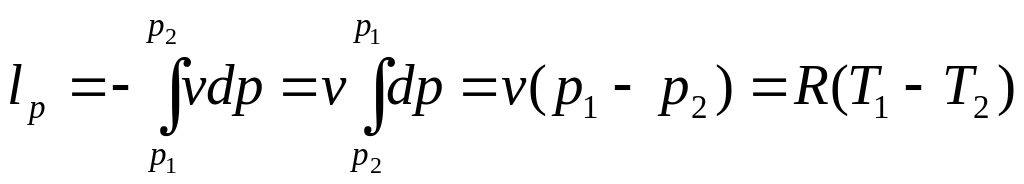. (2.3)

Теплота процесса:

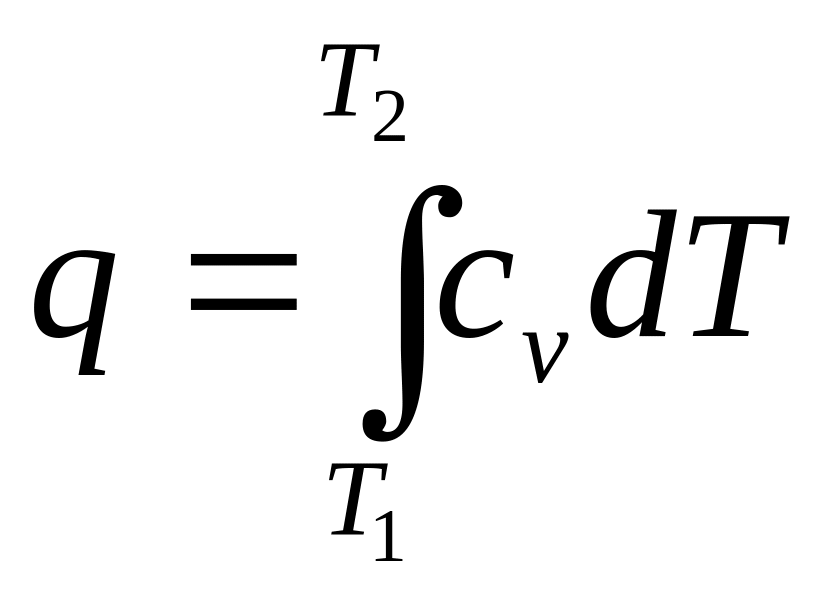. (2.4)

При : . (2.5)

. (2.7)

Изменение термодинамических функций:

. (2.8)

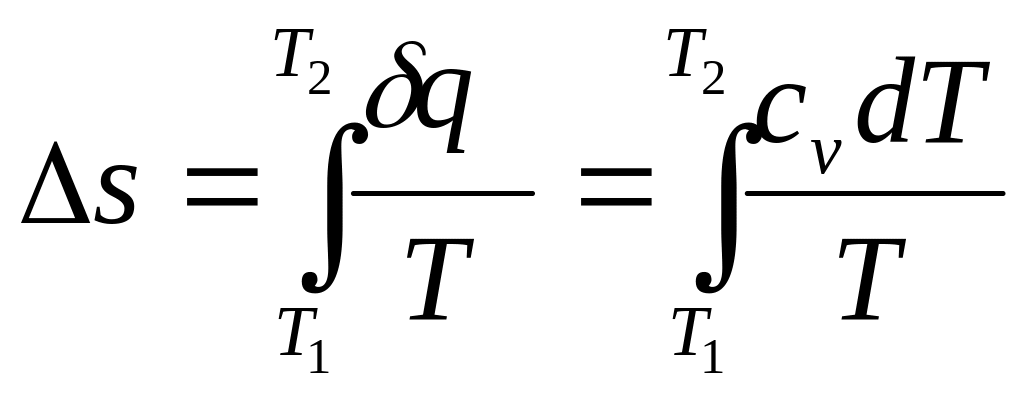. (2.9)

При : , (2.10)

Изобарный процесс – процесс, протекающий при постоянном давлении:

, . n=0.

Уравнение, связывающее параметры начального и конечного состояний:

, , . (2.13)

Работа процесса:

. (2.14)

Располагаемая работа: 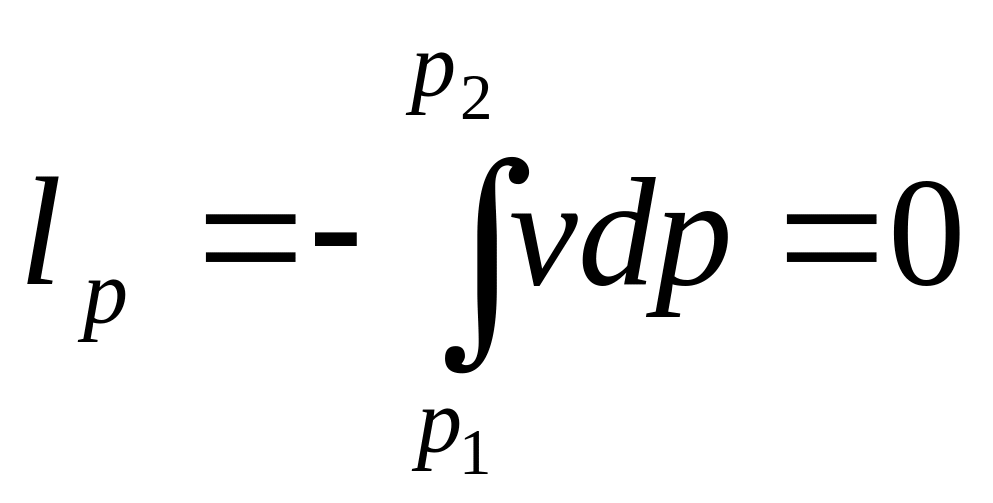. (2.15)

Теплота процесса:

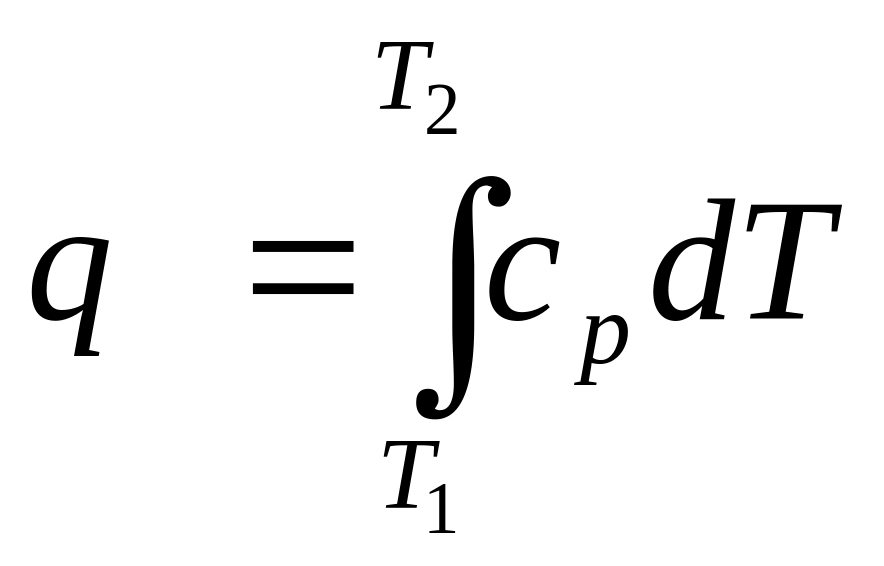, . (2.16)

При : . (2.17)

Изменение термодинамических функций:

, . (2.20)

Изменение энтропии в изобарном процессе:

. (2.23)

Изотермический процесс – процесс, протекающий при постоянной температуре: . n=1

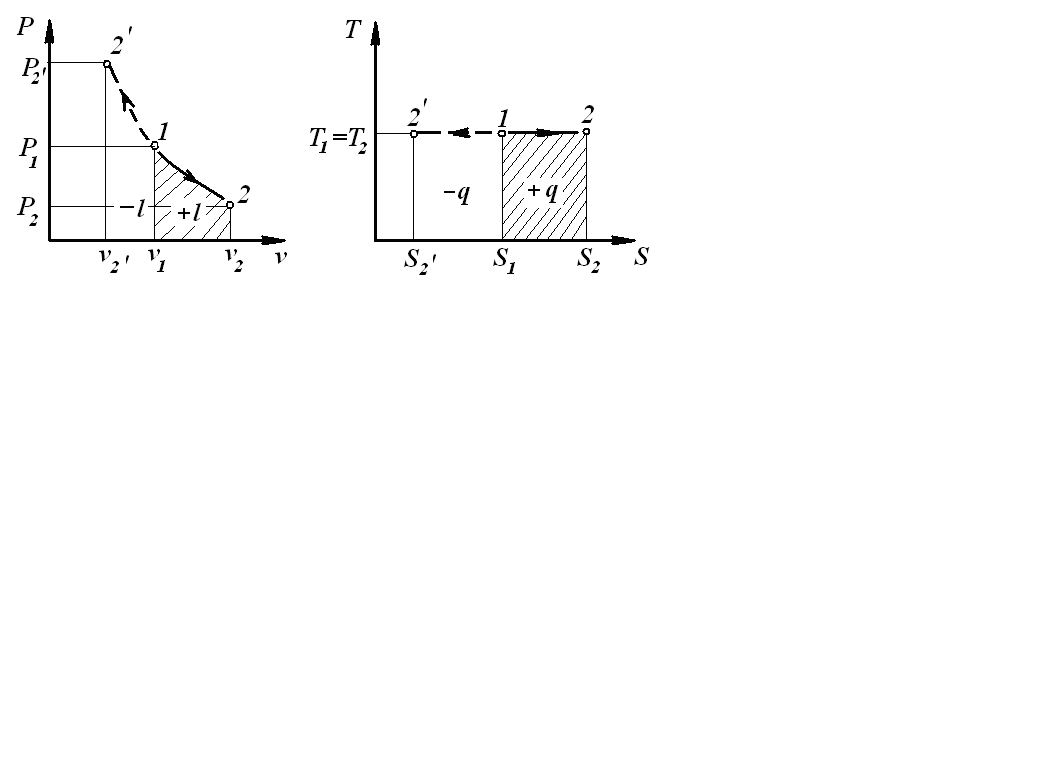
Уравнение, связывающее параметры начального и конечного состояний:

, . (2.26)

Работа процесса:

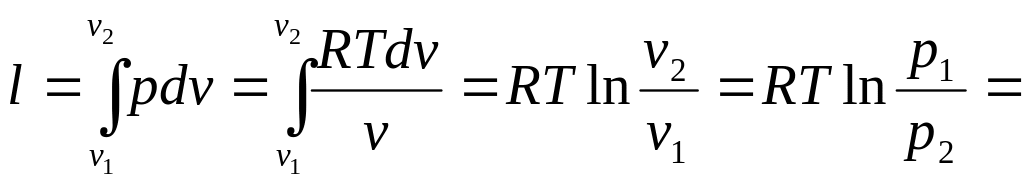
. (2.27)

Располагаемая работа:

(2.28)

Теплота процесса (с учетом того, что при для идеального газа ):

(2.29)

Изменение термодинамических функций:

, (2.30)

(2.31)

Адиабатный (изоэнтропный) процесс – процесс, протекающий без теплообмена с окружающей средой.

Уравнения, связывающие параметры начального и конечного состояний:

,

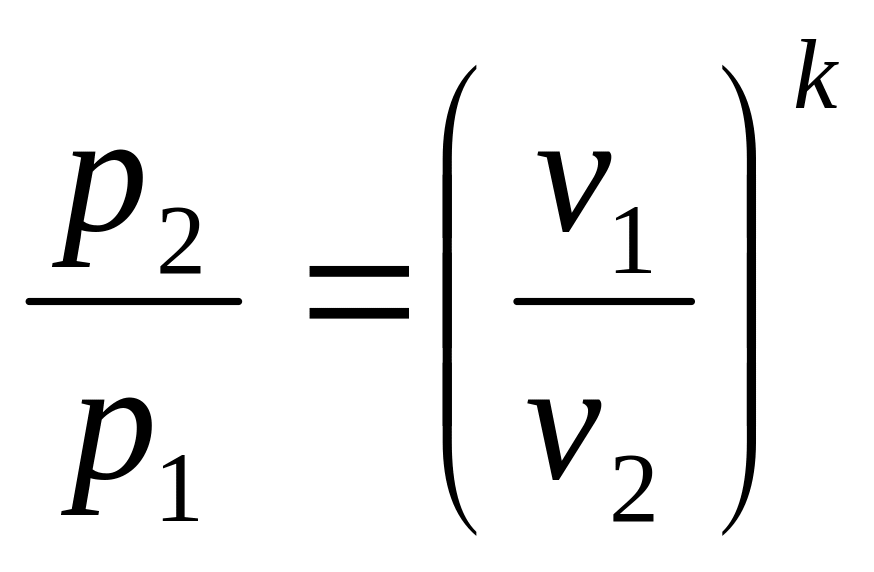. (2.32)

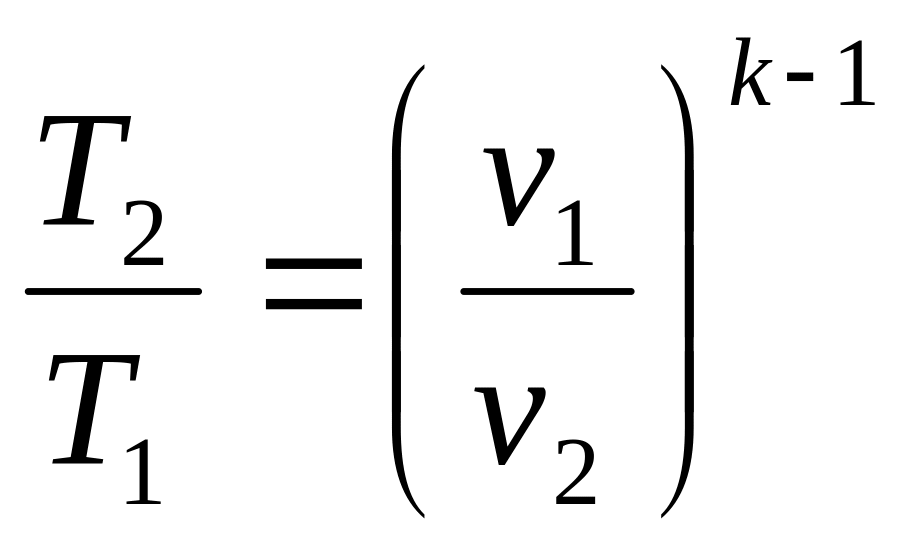, . (2.33)

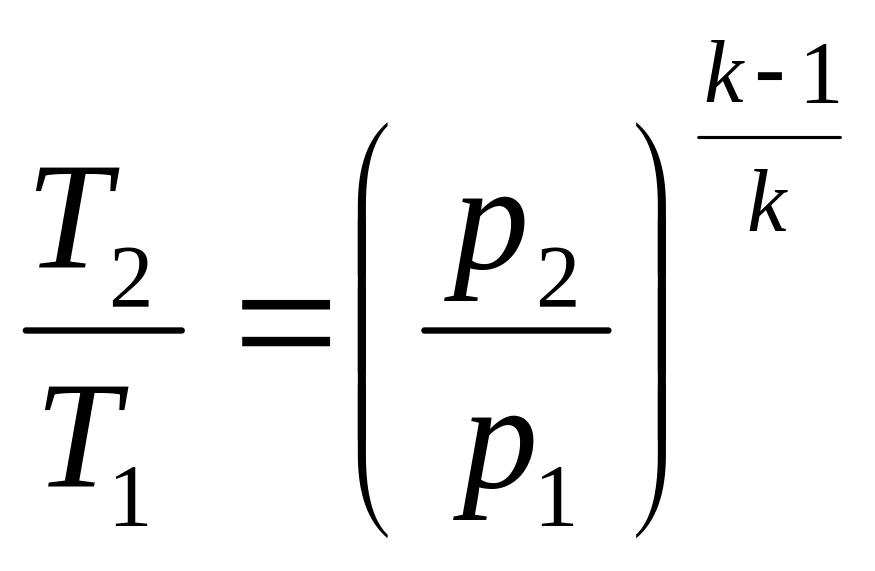, . (2.34)

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором не происходит процесс теплообмена системы с окружающими телами. С точки зрения первого начала термодинамики это означает, что работа совершается газом только за счет внутренней энергии:

q = ∆u + l = 0;

Работа процесса:

=

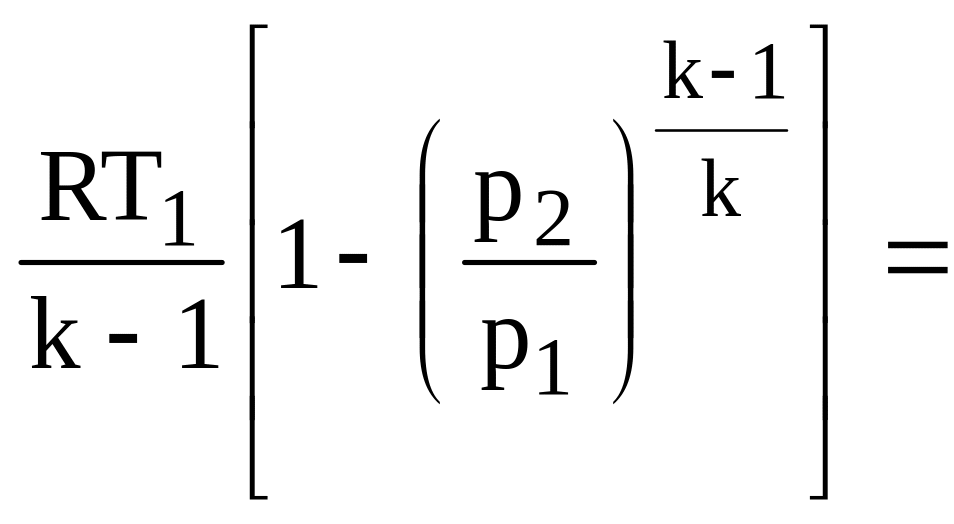
(2.35)

Располагаемая работа: . (2.36)

Теплота процесса: . (2.37)

И зменение термодинамических функций:

, (2.38)

, . (2.39)

График адиабатного процесса — более крутая кривая, чем гипербола при изотермическом процессе. Это объясняется тем, что при адиабатическом сжатии 1—3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Политропный процесс – процесс, протекающий при постоянной теплоемкости =const и удовлетворяющий уравнению:

(2.42)

где - показатель политропы .

Это уравнение отличается от уравнения адиабаты (2.30) только показателем степени ( вместо ). Поэтому уравнения для параметров и работы процесса получаются из уравнений (2.30) – (2.34) заменой на .

Соотношение параметров в процессе:

Теплота процесса:

, (2.43)

где теплоемкость политропного процесса:

(2.44)

Изменение термодинамических функций:

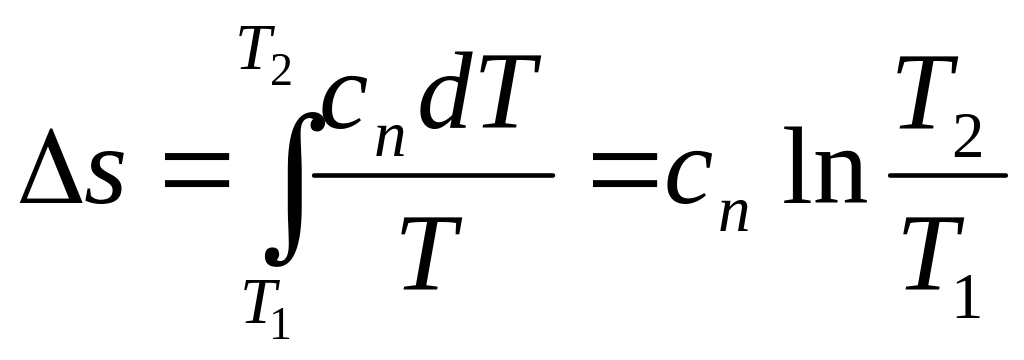, , (2.45)

Работа расширения /сжатия в политропном процессе. dl =pdv ,

.

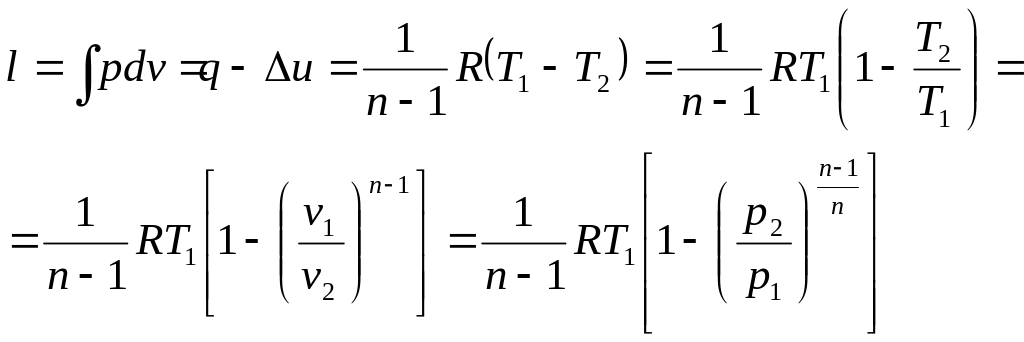Располагаемая работа

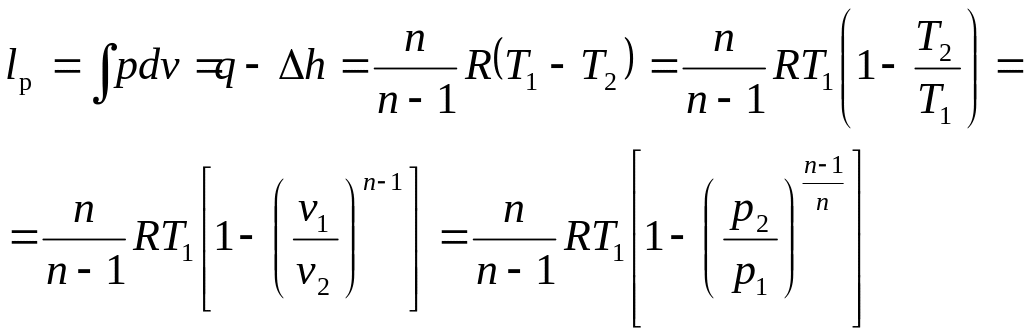
Обобщенная диаграмма политропных процессов.

Для анализа политропных процессов удобно пользоваться обобщенной диаграммой. На ней изображаются все изопроцессы и выделяются области, в пределах которых знаки слагаемых I закона одинаковы.

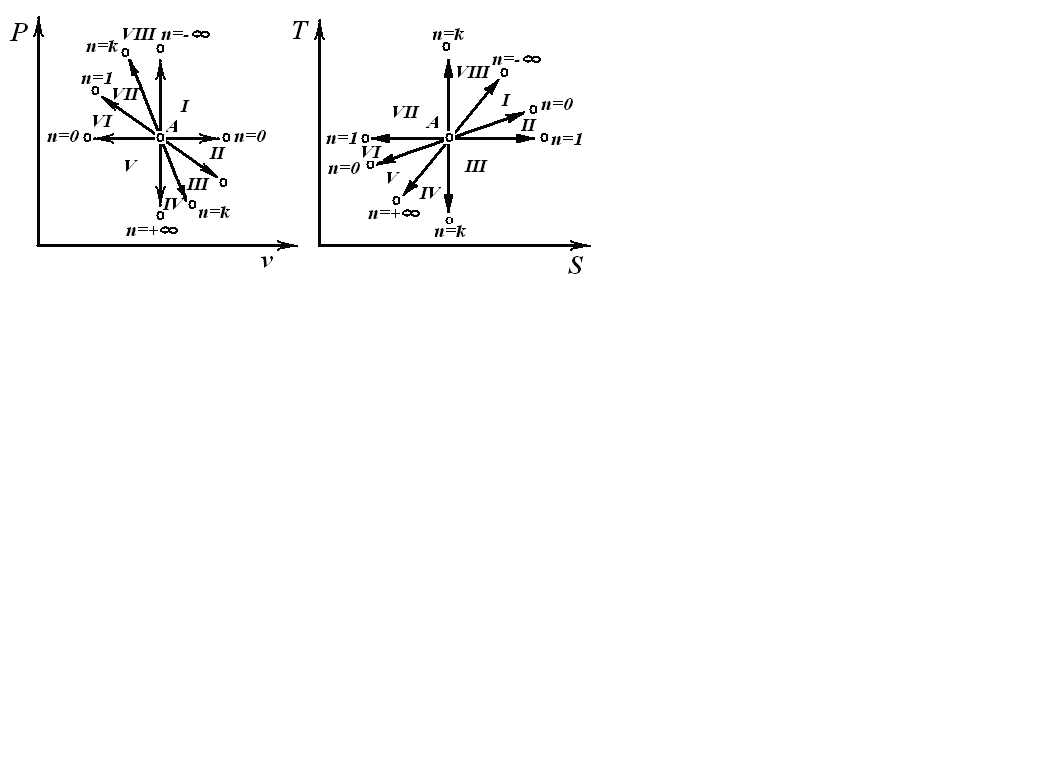
Области:

I÷IV – розширение рабочего тела, работа позитивна;

V÷VIII – сжатие рабочого тела, работа негативна;

I÷III,VIII – подвод теплоты к системе;

IV÷VIII – отвод теплоты от системы;

VII, VIII, I, II – повышение температуры системы;

III, IV, V, VI – понижение температуры системы.

Лекция