Метод трапеций
Формула трапеций имеет следующий вид:
(6)
Эта формула означает, что площадь криволинейной трапеции заменяется площадью многоугольника, составленного из п трапеций (рис. 5), при этом кривая заменяется вписанной в нее ломаной.
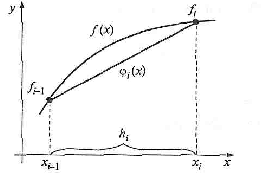
Рис. 5. Метод трапеций
Пример 5. Пользуясь формулой трапеций, вычислить определенный интеграл
при n
= 4.
Решение
Подынтегральная функция
на отрезке [0; 1] равна F(x)
=
.
Находим шаг вычислений
Отсюда точки интегрирования:
х0 = 0; х1 = 0,25; х2 = 0,5; х3 = 0,75; х4 = 1.
Тогда по формуле трапеций имеем
Ответ: = 0,764.
Пример 6. Методом трапеций вычислить определенный интеграл
Программа_________________________________________________
program integral; {метод трапеций}
uses crt;
var i,n:integer;
a,b,h,x,s:real;
function f(x:real):real;
begin
f:=(l/x)*sin(3.14*x/2);
end;
begin
clrscr; gotoxy(10,10);
textbackground(l); clrscr;
write('Введите нижний предел интегрирования');
readln(a); gotoxy(10,12);
write('Введите верхний предел интегрирования ');
readln(b); gotoxy(10,14);
write('Введите количество отрезков '); readln(n);
h:=(b-a)/n; s:=0; х:=а;
for i:=l to n-1 do
begin
x:=x+h; s:=s+f(x);
end;
s:=h*((f(a)+f(b))/2+s);
gotoxy( 10,18);
writeln('Интеграл равен' ,s:11:4);
readkey;
end.
Метод Симпсона
Геометрически иллюстрация формулы Симпсона состоит в том, что на каждом из сдвоенных частичных отрезков заменяем дугу данной кривой дугой графика квадратного трехчлена (рис. 7).
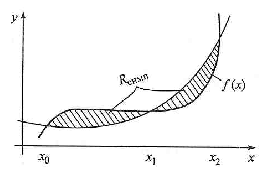
Рис. 7. Метод Симпсона
Разобьем отрезок интегрирования [a;
b] на 2n
равных частей длиной
.
Обозначим точки разбиения х0
= а; х1 = х0 +
h, ..., хi
= х0 + ih,
..., х2n =
b. Значения функции
f в точках xi
обозначим уi,
т. е. yi=f(хi).
Тогда, согласно методу Симпсона
Пример 7. Вычислить определенный интеграл по формуле Симпсона
при h = 0,25.
Решение
Вычислим значения подынтегральной функции f(x) = в точках
х0 = 0; х1 = 0,25; х2 = 0,5; х3 = 0,75; x4= 1,
получим
Ответ:
=0,702.
Пример 8. Вычислить
интеграл I
=
,
п = 10
методом Симпсона, где
п –
количество разбиений отрезка
интегрирования.
Решение
Имеем п = 10, отсюда h=
=
0,1. Результаты вычислений приведены в
таблице.
i |
хi |
y2j-1 |
y2j |
0 |
0 |
|
y0 = 1,00000 |
1 |
0,1 |
0,90909 |
|
2 |
0,2 |
|
0,83333 |
3 |
0,3 |
0,76923 |
|
4 |
0,4 |
|
0,71429 |
5 |
0,5 |
0,66667 |
|
6 |
0,6 |
|
0,62500 |
7 |
0,7 |
0,58824 |
|
8 |
0,8 |
|
0,55556 |
9 |
0,9 |
0,52632, |
|
10 |
1,0 |
|
0,50000 = уn |
|
|
3,45955( |
2,72818( |
)
2)
По формуле Симпсона получаем:
Подсчитаем погрешность полученного результата. Полная погрешность R складывается из погрешностей действий R1 и остаточного члена R2. Очевидно
где A(i)
— коэффициенты формулы
Симпсона;
— максимальная ошибка округления
значений подынтегральной функции.
Тогда
R1 = п * h * .
Программа_____________________________________________________
Procedure INTEGR (var S:real; K:integer); {Метод Симпсона}
begin
S := 0.0; X := A;
IF K<5 THEN FOR I := 0 TO N DO
begin
IF К<>З THEN X:=A+H*I ELSE X:=A+H/2+H*I;
F := FUNC (X);
IF K=4 THEN F := F/2.0;
IF (1=0) AND (K<>2) THEN S := S + F;
IF (I=N) AND ((K=2) OR (K=4)) THEN S := S + F;
IF(K>0) AND (ION) THEN
IF K<>4 THEN S := S+F ELSE S := S + F*2;
end
ELSE
begin
FOR I := 1 TO N-l DO
S := 2*FUNC(X+H*I) + 4*FUNC(X+H*I-H/2) + S;
S := S + 4*FUNC(B-H/2) + FUNC(A) + FUNC(B); S := S / 6; end;
S := S * H; end;
Пример 9. Вычислить интеграл методом Симпсона
Программа_____________________________________________________
Program integral; {Метод Симпсона}
Uses crt;
var i,n,c:integer;
a,b,h,x,s:real;
function f(x:real):real;
begin
f:=(l/x)*sin(Pi*x/2);
end;
begin
clrscr; gotoxy(10,10);
textbackground(l); clrscr;
write('Введите нижний предел интегрирования ');
readln(a); gotoxy(10,12);
write('Введите верхний предел интегрирования ');
readln(b); gotoxy(10,14);
write('Введите количество отрезков '); readln(n);
h:=(b-a)/n; s:=0; х:=а; с:=1;
for i:=l to n-1 do
begin
x:=x+h; s:=s+(3+c)*f(x); c:=-c;
end;
s:=h*(f(a)+f(b)+s)/3; gotoxy(10,18);
write('Интеграл равен ',s: 11:5);
readln;
end.
Пример 13.
Вычислить интеграл
методами трапеций и Симпсона.
Программа_____________________________________________________
program tr_s;
uses crt, graph;
var
a,b:real; { Границы отрезка }
r,r2:real; { Предыдущее и текущее значения интеграла}
minteger; { Счетчик }
{ Интегрируемая функция }
function f(x:real):real;
begin
f:=0.43429/(x*ln(x));
end;
{ Метод трапеций }
function trap(a,b:real;n:integer):real;
var
s:real; {Сумма }
h:real; { Шаг }
rminteger; { Счетчик } begin
h:=(b-a)/(n-I);
s:=(f(a)+f(b))/2; { Начальное значение суммы }
for m:=l to n-2 do s:=s+f(a+m*h);
trap:=s*h; {Значение интеграла }
end;
{ Метод Симпсона }
function simpson(a,b:real;n:integer):reaI;
var
s:real; { Сумма }
h:real; { Шаг }
mrinteger; { Счетчик }
mminteger; { Очередной множитель } begin
h:=(b-a)/(n-l); {Вычисление шаг}
s:=f(a)+f(b); { Начальное значение шага }
mn:=4; { Первый множитель }
{ Суммирование остальных элементов }
for m:=l to n-2 do
begin
s:=s+mn*f(a+h*m);
if(mn=4) then mn:=2 else mn:=4;
end;
simpson:=s*h/3; { Вычисленное значение }
end;
Begin
clrscr;
\угке('Введите нижний предел интегрирования ');
readln(a);
у/гке('Введите верхний предел интегрирования ');
readln(b);
write('Введите количество отрезков '); readln(n);
writeln('Интeгpaл равен ', trap(a,b,n), simpson(a,b,n));
readln;
end.