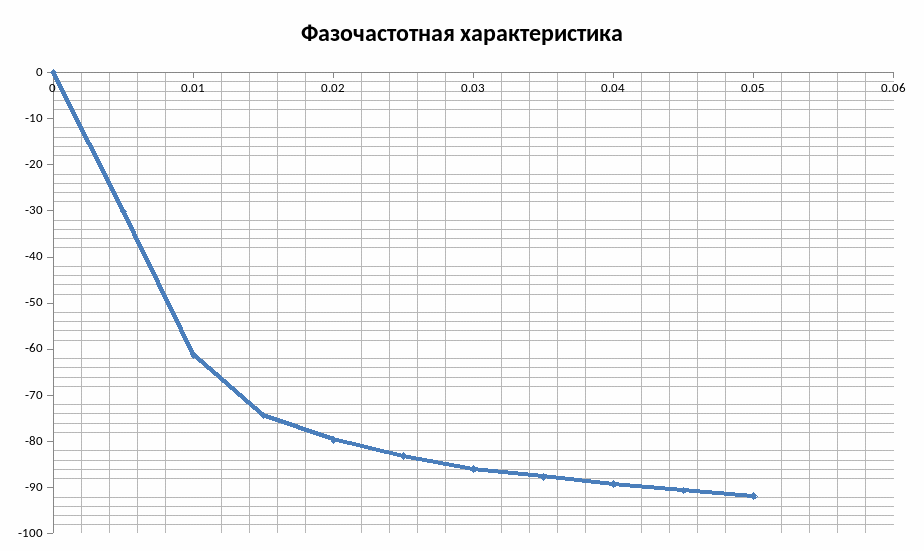
4.2Частотные характеристики объекта по каналу управления.

Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена, вызванные гармоническим воздействием на _входе.

Выражения частотных характеристик по каналу управления могут быть получены из выражения частотной передаточной функции.

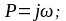
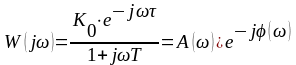
где А() - АЧХ объекта

() - ФЧХ объекта

Зависимость отношения амплитуд выходных и входных колебаний от их частоты называется амплитудно-частотной характеристикой (АЧХ). Зависимость разности фазы выходных и входных колебаний от частоты называется фазо-частотной характеристикой (ФЧХ) системы.

Найдем модуль частотной передаточной функции (АЧХ):

А(ω)= |К₀ |/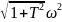 =|-5,5|/

()=-τ-аrctgT

Т.к. К₀ 0 ,то фыражение ФЧХ пишется в виде :

()=-π-τ-аrctgT

Частота _пр., определяющая полосу частот пропускания объекта, найдется из условия:

A(_пр)= А()_=0

A(_пр)= К₀

_пр = 1/Т = 1/180 = 0,005с ^-1

Частотные характеристики будем строить на диапазоне от 0 до 10-15 _пр.

Результаты расчетов сведена в таблицу 2.

Таблица 2

, с-1	0	0,005	0,01	0,015	0,02	0,025	0,03	0,035	0,04	0,045	0,05
АЧХ,	5,5	4,08	2,67	1,91	1,47	1,19	1,001	0,86	0,75	0,67	0,607
, рад.	0	-30,14	-61,25	-74,31	-79,61	-83,11	-85,94	-87,62	-89,23	-90,6	-91,79

По данным таблицы 2 построены графики АЧХ и ФЧХ.

Из графика АЧХ видно,что чем меньше частота входного сигнала, тем больше этот сигнал усиливается.При ω=0 ,коэффициент усиления максимален и равен 5,5. При больших частотах выходная величина по модулю стремится к 0. Такие сигналы объект не пропустит.

5. Структурная схема системы регулирования

Структурная схема системы – графическое изображение АСР в виде совокупности динамических звеньев с указанием связей между ними.

Исходными данными для построения схемы служат передаточные функции звеньев.

Структурная схема системы регулирования

6.Параметрический анализ сау

6.1 Построение области устойчивости в плоскости варьируемых параметров

1. Передаточная функция разомкнутой системы равна:

_{W(p)=Wрег(Р)*Wим(Р)*Wр.о(Р)*Wоб(Р)*Wд(Р)=}

_{=(К1Р+К2)*Ким*Кро*К0 е-рτ *Кд / Р(1+ТР)}

_{Обозначим К=(К1Р+К2)*Ким*Кро*К0 е-рτ *Кд / Р(1+ТР) =}

_{=-5,5*124*0,0104*0,06=-0,425}

_{Тогда :}

_{W(p)= К е-рτ (К1Р+К2) / Р(1+ТР)}

_{2. Передаточная функция замкнутой системы по каналу управления :}

_{3. Передаточная функция замкнутой системы по возмущению :}

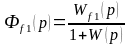
Характеристический полином замкнутой системы получим из выражения:

1+W(p)=1+Ке^-рτ(К₁+К₂) / Р(1+Тр)=0

_отсюда Д(р)=Тр²+р(1+К₁Ке^-рτ)+КК₂е^-рτ=0

_1.Уравнение апериодической границы устойчивости соответствует р=0.

Получаем: КК₂=0 или К₂=0

2.Граница ,соответствующая бесконечному корню отсутствует, так как Т не может быть равно нулю по условию.

3.Найдем колебательную границу устойчивости.Для этого подставим р=Јω.

Д(Јω)=-Тω²+ Јω(1+КК₁(cosωτ-Јsinωτ))+КК₂(cosωτ-Јsinωτ)

тогда:

U(ω)= -Тω²+ω КК₁sinωτ+КК₂ cosωτ=0

V(ω)= ω+ω КК₁cosωτ-КК₂ sinωτ=0

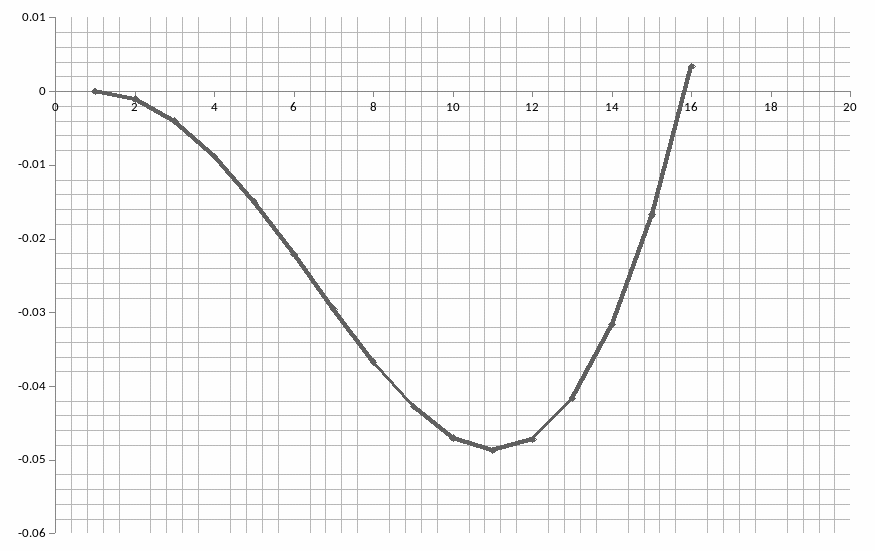
Решив уравнение относительно К₁ и К₂ , найдем выражение для колебательной границы устойчивости в виде:

К₁= Тω sinωτ- cosωτ / К

К₂= ω(sinωτ+ Тω cosωτ) / К

Рассчитаем 3 точки колебательной границы устойчивости при ω=0, ∆ω, 2∆ω.Результаты занесем в таблицу 3.

Таблица3.

 [c-1]	0	0,005	0,01
К1	2,3498	1,0415	-2,3105
К2	0	-0,0150	-0,0427

РЕЗУЛЬТАТЫ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ

ОДНОКОНТУРНОЙ ТИПОВОЙ НЕПРЕРЫВНОЙ АВТОМАТИЧЕСКОЙ СИСТЕМЫ

14.10.10

********************************************************************

ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ :

(апериодическое звено 1-го порядка с запаздыванием)

K * Exp(-Tau*P)

W(P) = ----------------- .

1 + T*P

ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :

Коэффициент передачи K = -5.500

Постоянная времени T = 180.000

Запаздывание Tau = 100.000

********************************************************************

ПЕРЕДАТОЧНАЯ ФУНКЦИЯ РЕГУЛЯТОРА С ПИ - ЗАКОНОМ УПРАВЛЕНИЯ:

K1*P + K2

W(P) = --------------- .

P

НАСТРОЙКИ РЕГУЛЯТОРА :

K1 - ПРОПОРЦИОНАЛЬНАЯ СОСТАВЛЯЮЩАЯ ;

К2 - ИНТЕГРАЛЬНАЯ СОСТАВЛЯЮЩАЯ .

********************************************************************

ЭЛЕМЕНТОВ СИСТЕМЫ УПРАВЛЕНИЯ - УСИЛИТЕЛЬНЫЕ ЗВЕНЬЯ .

ПАРАМЕТРЫ ЭЛЕМЕНТОВ:

Коэффициент передачи ДАТЧИКА   0.060

Коэффициент передачи ИСПОЛНИТЕЛЬНОГО МЕХАНИЗМА 124.000

Коэффициент передачи РЕГУЛИРУЮЩЕГО ОРГАНА 0.010

********************************************************************

РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ

НЕПРЕРЫВНОЙ ЛИНЕЙНОЙ СИСТЕМЫ

В ПЛОСКОСТИ ПАРАМЕТРОВ К1 и К2 ПИ-РЕГУЛЯТОР

УРАВНЕНИЯ ГРАНИЦ ОБЛАСТИ:

АПЕРИОДИЧЕСКАЯ ГРАНИЦА - К2 < 0 ,

КОЛЕБАТЕЛЬНАЯ ГРАНИЦА УСТОЙЧИВОСТИ ЗАДАЕТСЯ В ВИДЕ ТАБЛИЦЫ

W K1 K2

0,0000 2,3498 0,0000

0,0013 2,2651 -0,0010

0,0025 2,0133 -0,0040

0,0038 1,6016 -0,0088

0,0050 1,0415 -0,0150

0,0063 0,3488 -0,0221

0,0075 -0,4567 -0,0295

0,0088 -1,3519 -0,0367

0,0100 -2,3105 -0,0427

0,0113 -3,3042 -0,0470

0,0125 -4,3029 -0,0487

0,0138 -5,2754 -0,0472

0,0150 -6,1905 -0,0416

0,0163 -7,0173 -0,0316

0,0175 -7,7262 -0,0167

0,0188 -8,2897 0,0034

0,0201 -8,6829 0,0289

_{Область устойчивости системы в плоскости варьируемых параметров}

Определение направления вида.штриховки колебательной границы устойчивости производится в соответствии со знаком определителя вида

()= == =

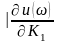
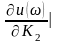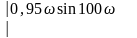
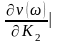
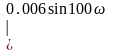
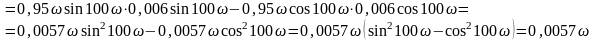
При перемещении вдоль колебательной границы в направлении возрастании частоты от 0 до  кривая штрихуется слева, т. к.  > 0. Если частоту менять в пределах от -  до 0 ( < 0), то определитель меняет знак и, двигаясь вдоль увеличения частоты, нужно штриховать правую часть кривой. Таким образом, кривая колебательной границы проходится дважды, при этом штрихуется одна и та же часть кривой двойной штриховкой. Апериодическая граница устойчивости штрихуется в сторону колебательной границы устойчивости.

Параметры регулятора K₁ ,K₂, выбранные из области устойчивости системы, обеспечат затухание переходной составляющей её движения при любых начальных отклонениях и внешних воздействиях.Однако это недостаточно для оценки системы с точки зрения её практической пригодности