2.2.4. Фрактальні параметри рельєфу

Рельєф реальних шорстких поверхонь можна класифікувати за значеннями фрактальної розмірності D_f, яка характеризує складність форми рельєфу. Значення D_f для поверхні лежить у межах від 2 до 3:

D_f = 2 – фрактал, що відповідає диференційованій гладкій поверхні;

D_f = 2,5 – броунівський фрактал (форма рельєфу складна);

D_f = 3 – "екстремальний" фрактал (найскладніша форма рельєфу).

Для реальних поверхонь D_f2,5.

2.3. Метричні моделі мікрогеометрії поверхні

У метричному (класичному) підході до опису мікрогеометрії поверхні рельєф і профіль описуються як функції z(x,y) та у(x) відповідно. Проте в різних методах діагностики поверхні, а саме при реконструкції профілю у(x), інтенсивність та напрям відбитого сигналу визначається в першу чергу не висотами, а значеннями нахилів окремих ділянок профілю поверхні [9]. Тому розглянемо більш детально кутовий розподіл профілю поверхні.

У кожній точці x профілю існує похідна

. (2.16)

Отже, до кожної точки профілю можна провести дотичну. Позначимо через γ(х) кут нахилу дотичної в точці х відносно середньої лінії, тоді .

Для гладких поверхонь із класом чистоти поверхні вище 12 (табл. 2.1) середнє значення <1, тому вираз для нахилів можна записати у вигляді

. (2.17)

У наближенні геометричної оптики профіль поверхні подається набором мікроплощадок, де нахил кожної з них дорівнює нахилу дотичної γ(х). Параметри функції γ(х) визначаються за формулами (2.1)-(2.6) аналогічно до параметрів профілю, після заміни функції у(х) на γ(х). Наприклад, досить часто використовується середньоквадратичний нахил профілю R_dq (або σ_γ), який визначається формулою, аналогічною до (2.4).

Нахили поверхні можна також описати функцією розподілу нахилів (гістограмою нахилів) F_r(γ), яка фізично означає ймовірність нахилу мікроплощадки під кутом γ. Ця функція визначається як відношення довжини профілю S(,+) з елементарними ділянками, що знаходяться в кутовому інтервалі (,+), до повної довжини профілю S₀, тобто

. (2.18)

За визначенням, для функції розподілу нахилів F_r(γ) можна записати умову нормування

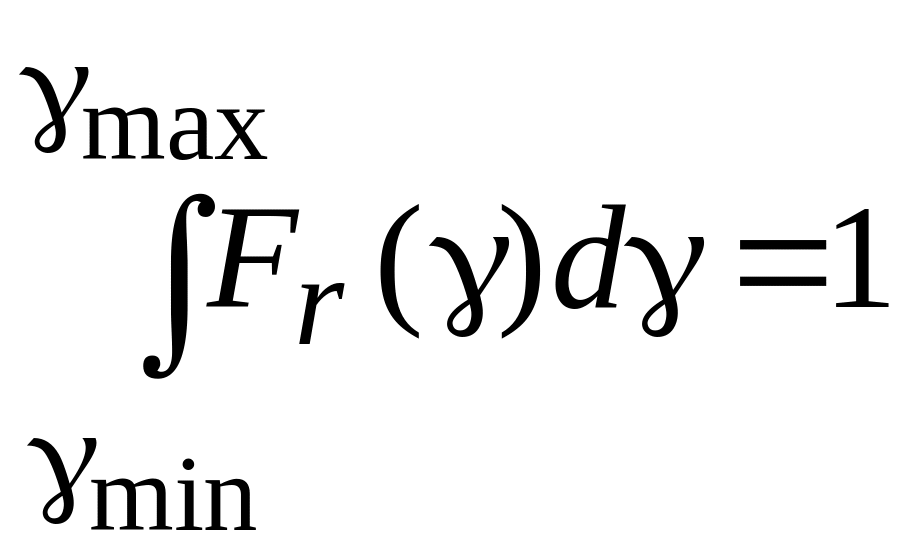, (2.19)

де γ_min, γ_max – відповідно мінімальне та максимальне значення нахилу.

Виразимо значення функції розподілу нахилів F_r(γ) через функцію нахилів γ(х). Для цього знайдемо функцію х(γ), обернену до γ(х). Похідна оберненої функції х(γ)

. (2.20)

Тоді функція розподілу нахилів визначається виразом

. (2.21)

Отже, функцію F_r(γ) можна отримати з відомої функції профілю y(x) в такий спосіб:

. (2.22)

Водночас отримання функції профілю у(х) через функцію F_r(γ) у загальному випадку неможливе, проте профілі реальних поверхонь можна описати за допомогою кількох моделей і для кожної моделі обчислити функцію нахилів γ(х) та функцію розподілу нахилів F_r(γ). В частковому випадку, коли розглядається певна модель профілю, можна відновити профіль у(х) через F_r(γ). Розглянемо деякі з моделей профілю, які відносно просто дозволяють досить точно описувати реальні поверхні зразків.