2.1.2. Просторові (крокові) метричні параметри профілю
Властивості шорсткої поверхні визначаються не тільки висотою нерівностей, а також відстанню (кроком) між нерівностями, тому розглянемо наступні просторові параметри:
1. Автокореляційна функція, за визначенням [2, 4], дорівнює
,
(2.7)
де Δх – зсув функції; символ Е означає просторове усереднення за обмеженою областю. Автокореляційна функція АСF – це детермінована характеристика ступеня періодичності профілю. Автокореляційну функцію характеризує кореляційна довжина (кореляційний інтервал) La, що, за визначенням, обмежує простір, всередині якого існує статистична когерентність процесу. Умовно за межу цього інтервалу приймають значення, при якому автокореляційна функція зменшується в е разів від максимального значення.
2. Розподіл амплітуд просторових частот C(f) у складній періодичній структурі профілю (спектр профілю в комплексній формі) визначається як дискретне Фур'є-перетворення функції у(xk) уздовж лінії довжиною L, що містить n точок профілю [5]
,
(2.8а)
де і – уявна одиниця; f – просторова частота, яка змінюється в межах від 0 до n/2L. Крім частоти f, використовується також період гармоніки T=1/f.
Отримати спектр просторових частот профілю можна й без використання комплексних чисел. У більшості випадків профіль у(x) шорсткої поверхні можна вважати неперервною функцією, що визначена на проміжку (а, b). Таку функцію можна розкласти у збіжний ряд Фур'є на проміжку (a, b) за формулою:
,
(2.8б)
де
,
.
Кількість гармонік
обмежують залежно від точності розкладу
профілю в спектр просторових частот,
якщо профіль визначений в n
точках, то кількість гармонік вибирається
n/2. Коефіцієнти ряду
Фур'є ak
та bk
знаходять зазвичай методом Сімпсона
[6]. Гармоніка з номером k
має період
або
частоту
.
Ряд Фур'є (2.8б) також можна записати тільки для синусів [5] у вигляді
,
(2.8в)
де
– амплітуда гармоніки;
– фаза.
При перетворенні Фур'є профіль поверхні задається сумою гармонік, які описують нерівності поверхні з різними горизонтальними розмірами. При цьому гармоніки з малими номерами k (низькочастотні) описують нерівності з великими горизонтальними розмірами, а гармоніки з великими значеннями номера k (високочастотні) описують нерівності з малими горизонтальними розмірами.
Використовуючи розклад у ряд Фур'є, можна оцінити періодичність профілю. Для періодичних профілів (рис.2.4а) існує одна гармоніка (синусоїда) з максимальною амплітудою (крім гармоніки з нульової частотою, яка відповідає постійній складовій профілю). Вона описує періодичну складову профілю. Для профілів із менш вираженою періодич-ністю (рис.2.4б), крім однієї гармоніки з максимальною амплітудою (періодична складова), існує також багато гармонік зі значними амплітудами (неперіодична складова).
3. Середній крок нерівностей профілю Sm (середня відстань між нерівностями). У випадку синусоїдального профілю Sm, очевидно, дорівнює періоду синусоїди. Крокові параметри дають інформацію про щільність розподілу нерівностей на поверхні [3].
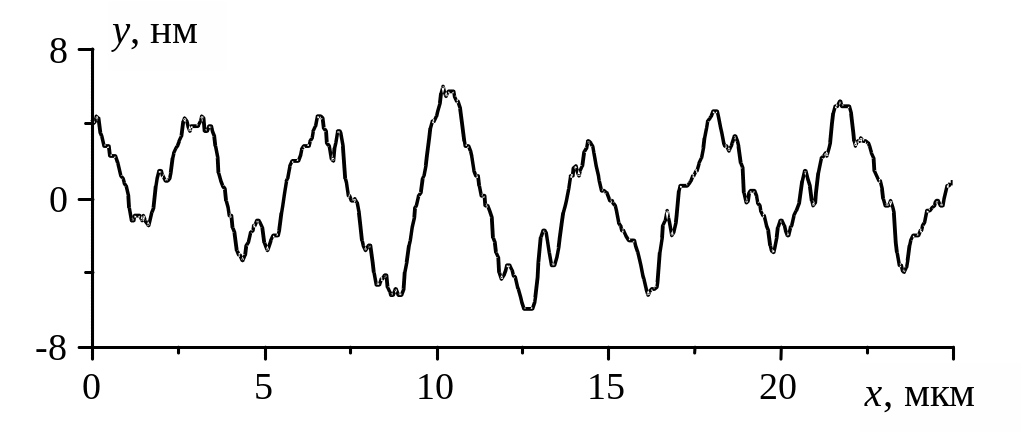а
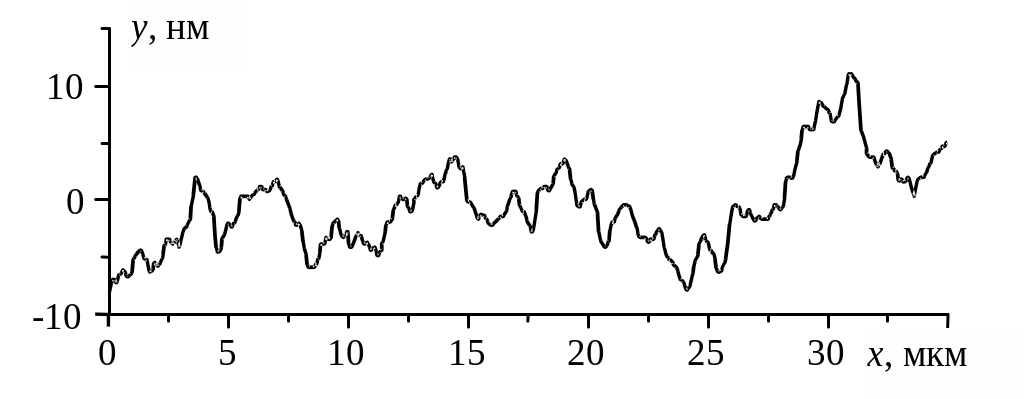б
Рис. 2.4. Розклад у ряд Фур'є профілю поверхні: а) ряд Фур'є та профіль для зразка GaAs №1 (періодичний профіль); б) ряд Фур'є та профіль для зразка GaAs №2 (профіль, близький до періодичного)