6. Связь между критерием устойчивости Попова с критерием устойчивости Найквиста
(19)
Из (19): 
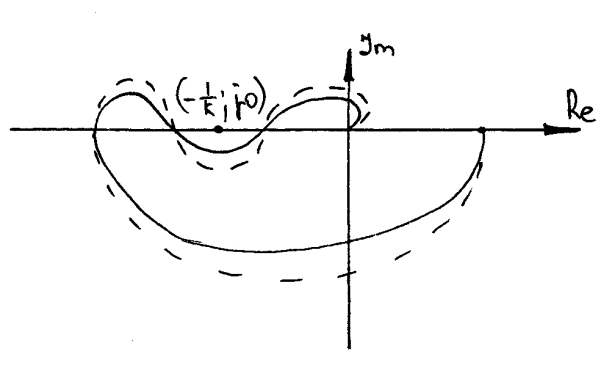
По Найквисту устойчива, по Попову – нет. Т.е. критерий Попова предполагает устойчивость с некоторым запасом.
Приближенные методы исследования нелинейных систем
Идея метода гармонической линеаризации
Важную информацию о существовании периодических режимов в нелинейных системах, их числе и параметрах может дать приближенный метод гармонической линеаризации. Достоинство частотного метода гармонической линеаризации заключается в его наглядности и в возможности получения зависимости показателей качества процессов от вида и параметров нелинейности, структуры и параметров линейной системы. Отсутствуют ограничения, накладываемые на порядок дифференциальных уравнений, описывающих динамику системы.
Рассмотрим нелинейную систему, структурная схема которой представлена на рис. 29.
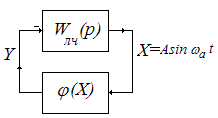
Рис.29. Нелинейная система I рода
Система состоит
из линейной части с передаточной функцией
и нелинейного элемента с характеристикой
.
Входная величина X
нелинейного элемента и выходная Y
являются периодическими функциями
времени. Метод
гармонической линеаризации основан на
предположении, что колебания на входе
нелинейного элемента являются
синусоидальными,
то есть
,
(19)
где А
– амплитуда,
- частота этих колебаний (рис.30).
Рис.30. Прохождение гармонического колебания
через нелинейное звено
В действительности автоколебания в нелинейных системах всегда несинусоидальны вследствие искажения их формы нелинейным элементом. Поэтому указанное выше предположение означает, что метод гармонической линеаризации является приближенным и область его применения ограниченна.
Достоверность результатов исследования этим методом напрямую зависит от следующего условия:
Линейная часть системы должна являться фильтром низких частот. АЧХ линейной части системы в этом случае имеет вид, как на рис.31.
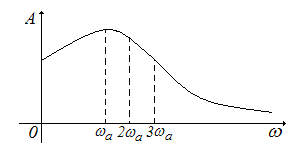
Рис.31. Вид АЧХ линейной части системы
Наибольшую амплитуду будет иметь первая гармоника. Чем выше частота автоколебаний, тем в меньшей степени линейная часть системы вследствие своей инерционности реагирует на высокочастотный сигнал. В силу этого обстоятельства высокочастотными составляющими сигнала на выходе линейной части можно пренебречь.
Если разложить выходные колебания Y(t) в ряд Фурье и отбросить высшие гармоники, получим следующее выражение:
+
высшие гармоники (20)
Здесь
, (21)
где
(22)
Продифференцировав это равенство, получаем:
(23)
Подставив выражения (22) и (23) в выражение (20) получим следующее:
(24)
Соответственно,
(25)
Коэффициенты
и
называются коэффициентами гармонической
линеаризации. Они определяются видом
нелинейности
и значениями А
и
.
Постоянная составляющая
присутствует в уравнении (24) только для
нелинейностей несимметричных относительно
начала координат. Коэффициент
равен нулю только в случае однозначных
статических характеристик нелинейных
элементов. Неоднозначность характеристик
приводит к тому, что при изменении знака
входного сигнала происходит запаздывание
в изменении выходного сигнала в связи
с переходом на другую ветвь характеристики
.
В результате при гармоническом входном
воздействии возникает запаздывание по
фазе первой гармоники на выходе
относительно входного сигнала. Поэтому
в данном случае коэффициент
при косинусоидальной составляющей не
равен нулю и отрицателен. Соответственно
отрицательным будет и коэффициент
.
Таким образом, передаточная функция нелинейной части системы может быть описана следующей зависимостью:
.
(26)
Рассмотрим пример вычисления коэффициентов гармонической линеаризации для идеального реле.
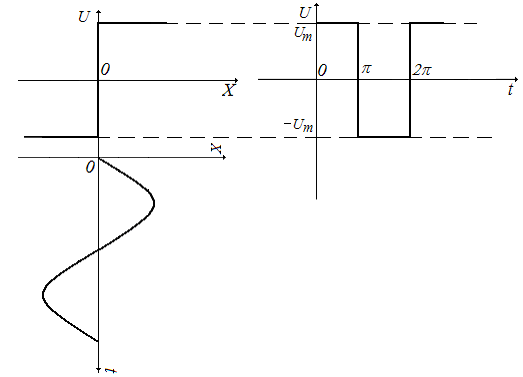
Рис.32. Прохождение гармонического сигнала через идеальное реле
Для того, что найти
коэффициенты
и
необходимо вычислить значения
и
:
;
,
здесь
Видно, что
коэффициент гармонической линеаризации
зависит от величины
- амплитуды гармонических автоколебаний
входного сигнала. В этом проявляется
нелинейность свойств данного звена.
Коэффициенты гармонической линеаризации для других типовых нелинейных звеньев вычисляются аналогично. Для решения задач можно воспользоваться готовыми справочными данными.