1. Особенности нелинейных систем автоматического управления

Нелинейной считается система, содержащая хотя бы одно нелинейное звено, то есть звено, описываемое нелинейным уравнением. Все реальные САУ в той или иной степени нелинейны, но часто существует возможность свести задачу к исследованию линейной модели реальной системы путем линеаризации последней. Процесс линеаризации невозможен в том случае, когда в системе присутствуют звенья с существенно нелинейными характеристиками.

Все реальные объекты и системы нелинейны.

Линейной называется такая САУ, которая описывается линейными дифференциальными уравнениями.

Е₁ R₂ E₂

R₁

I= ; I= *U; + - принцип суперпозиции в случае линейности.

Нелинейные объекты и системы – это те, у которых хотя бы один элемент нелинеен.

P = = K_об=( ) при I=I₁₀

Пример линеаризуемой (слабой) нелинейности.

Такая нелинейность присуща всем реальным объектам.

При К=К_min определяют точность, при К=K_max определяют устойчивость.

Но существуют такие нелинейности, которые нельзя линеаризовать (существенные).

Примеры:

1. Релейные элементы

u=sign εu_max ,т.е.

u

U_max

=u_max , при ε 0

u=-u_max , при ε 0

ε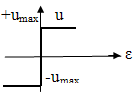

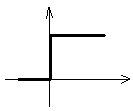с симметр. хар-кой с несимметр. хар-кой

2. Люфт:

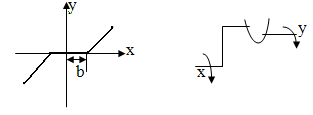
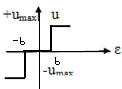
3. Гистерезис (неоднозначные нелинейные звенья):

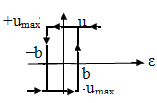u=u_max при ε≥b, если ε≥0

u=-u_max при ε b, если ε 0

4. Релейный элемент с зоной нечувствительности:

u=u_max при ε≥b

u=0 при -b ε b

u=-u_max при ε -b

Статические характеристики и математическое описание релейных элементов

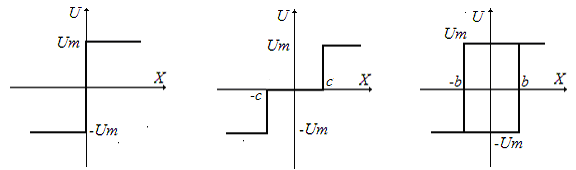
Рис. 1. Статические характеристики релейных элементов

а – идеальное реле;

б – реле с зоной нечувствительности;

в – реле с гистерезисом.

Выходной управляющий сигнал принимает следующие значения:

– для идеального реле

– для реле с зоной нечувствительности

– для реле с гистерезисом

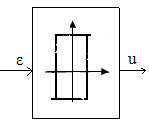
Нелинейные системы подразделяются на два класса. К нелинейным системам первого класса относят такие, которые с помощью структурных преобразований можно привести к виду (рис.2):

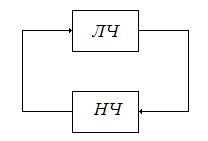
Рис.2. Нелинейные системы I класса

Системы, где подобное преобразование невозможно относят ко второму классу (рис.3). Они требуют использования более сложных с математической точки зрения методов исследования.

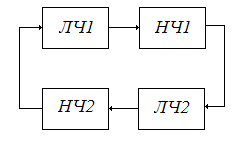
Рис.3. Нелинейные системы II класса

Методы исследования устойчивости нелинейных САУ

В линейной системе устойчивость обеспечивается тем, что в характеристическом уравнении замкнутой системы регулирования все корни имеют отрицательную вещественную часть, то есть лежат в левой полуплоскости.

Нелинейные системы имеют большое количество устойчивых, неустойчивых, полуустойчивых состояний.

абсолютно устойчивая система

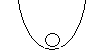
неустойчивая в большом и устойчивая в малом система (т.е. устойчива при малом отклонении и неустойчива при большом)

абсолютно неустойчивая система

Устойчивость и качество переходных процессов зависят от величины и вида внешнего воздействия

В линейных системах, где соблюдается принцип суперпозиции, устойчивость САУ не зависит от внешних воздействий и определяется параметрами только самой системы (рис. 4).

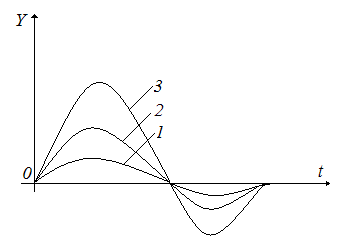
Рис.4. Переходные процессы в линейной системе

Колебательность и длительность переходного процесса не изменяются.

Период колебаний процесса в нелинейной системе не постоянен и изменяется по мере изменения отклонения (рис. 5).

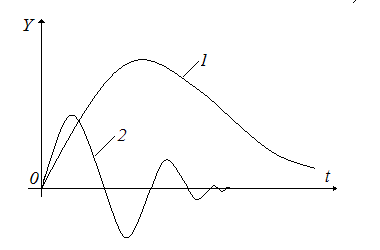
Рис.5. Переходные процессы в нелинейной системе

Кроме того, устойчивая при одних значениях внешних воздействий, нелинейная система может оказаться неустойчивой с возникновением расходящегося переходного процесса при других значениях этого воздействия или при других внешних воздействиях (рис. 6).

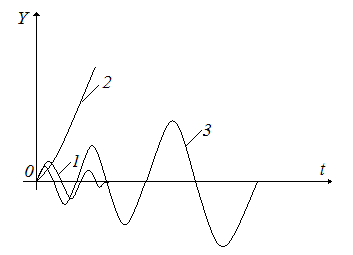
Для нелинейных систем характерен новый вид установившегося режима – режим автоколебаний

В линейных системах собственные незатухающие колебания возникают при нахождении системы на границе устойчивости. Их амплитуда пропорциональна величине внешнего воздействия. При этом, такая линейная САУ является неработоспособной. Появление автоколебаний в нелинейной системе еще не означает, что она не пригодна к эксплуатации. Этот случай проиллюстрирован на рис.7.

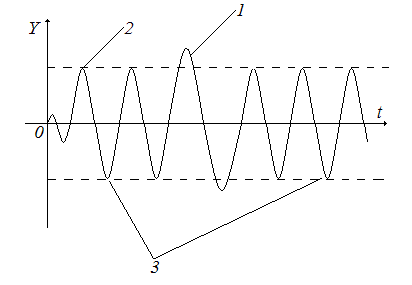
Рис.7. Режим автоколебаний

В области параметров можно выделить подобласти с многочастотными и одночастотными колебаниями.

Этот факт показан на рис.8..

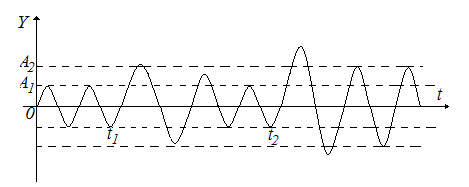
Рис.8. Автоколебания с различной амплитудой.

Таким образом, при рассмотрении вопроса устойчивости нелинейных систем необходимо оговаривать начальные условия и внешние воздействия. В отношении нелинейных систем нельзя говорить об устойчивости системы вообще, а только об устойчивости определенного динамического режима с жестко заданными параметрами.

При изучении нелинейных систем используют три понятия устойчивости.

Устойчивость в малом – это устойчивость при бесконечно малых отклонениях от исходного режима.

Устойчивость в большом – это устойчивость при конечных отклонениях, возможных в данной системе по условиям ее работы.

Устойчивость в целом – это устойчивость при неограниченных отклонениях, то есть при отсутствии каких-либо ограничений на них.

Нелинейная системах может быть устойчива в малом, но неустойчива в большом.