
- •Тест математика 2- й семестр
- •1 Исследуйте функцию на монотонность:
- •2. Найдите координаты точек экстремума функции
- •1.Вычислите площадь фигуры ограниченной линиями:
- •2.Вычислите интеграл:
- •3. Образующая конуса составляет с плоскостью основания угол в 450 . Найдите площадь полной поверхности конуса и объем, если его высота равна 6 см.
2.Вычислите интеграл:

а)2
; б) 3;
в) ; г)
-2.
; г)
-2.

а)9
; б) 7;
в) ; г)11.
; г)11.

а)5
; б)
 ;
в)
; г)
.
;
в)
; г)
.

а)3
; б)
 ;
в)
;
в) ; г)
.
; г)
.

а)2 ; б) 10; в) ; г) - .

а)0
; б) -1; в) ; г)2
; г)2

а)0 ; б) -1; в) ; г)2

а)18 ; б) 3; в) ; г)-4
 ,
,
а)8
; б)
 ; в)
; в) ; г)5
; г)5

а) ; б) 10;
в)18; г)
.
; б) 10;
в)18; г)
.

а)
8ln4; б)
4ln2
-
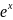 ;
в)e; г)8ln4
– 4 -
;
в)e; г)8ln4
– 4 -
 .
.
 ,
,
а)5; б)3 ; в) 9; г)4.
 ,
,
а)
2; б)
 ; в)
-
; г)
; в)
-
; г)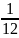 .
.
 .
.
а) 1; б) 2e +1; в)e; г)e - 1.
 ,
,
а) ; б)
;
в)6; г)
; б)
;
в)6; г) .
.
 ,
,
а)27 ; б) 64; в)20; г) 0.
 .
.
а)
 ; б)
; б)
 ; в)1; г)
0.
; в)1; г)
0.
 ,
,
а)
; б)
 ; в)1; г)
.
; в)1; г)
.

а)
; б)2
; в) ; г)
; г) .
.

а) ; б)
; б) ; в)
; в) ; г)
.
; г)
.
 ,
,
а)
-
; б)
 ; в)
; г)
; в)
; г) .
.
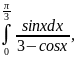
а) ; б)
; б) ; в)tg
; в)tg ; г)
.
; г)
.
 ,
,
а)
1 ; б) ; в) - 1; г)
.
; в) - 1; г)
.
 ,
,
а)
-
 ; б)
; б)
 ;
в)
;
в) ; г)
.
; г)
.
 ,
,
а)
е; б) е
– 1) ; в)
е
е
– 1) ; в)
е ; г)
; г) .
.
 .
.
а) -3
-3 ;б)2
;б)2 ; в)8
; г)8
; в)8
; г)8 .
.
Составьте уравнение касательной, проведенной к графику функции у=x – 3x2 в точке х0=2.
а)y= - 11x - 10; б)y = 13x + 10 ; в)y = -10x - 22; г)y = 4x + 13.
Составьте уравнение кривой, проходящей через точку М(1;4), если угловой коэффициент касательной к кривой в каждой ее точке равен 3х2-2х.
а)y= x3 +x2+4; б)y = 6x - 2 ; в)y = 10x3– 2x2; г)y = 4x + 13.
Точка движется прямолинейно с ускорением, а=12t2+6t. Найдите закон движения точки, если в момент времени t=1с. ее скорость v=8м/с, а путь s=6м.
а)s= t3 +t2+4;б)s = 24t +6 ; в)s = 24t; г)s = t4 +t3 +t + 3.
При каком значении α векторы а= 3i-5j+ᾳk и в= -4i-2j+k перпендикулярны?
а)2; б) -2 ; в)22; г) -22.
Тело брошено с поверхности земли вертикально вверх со скоростью v=(29,4- 9,8t)м/с. Найдите наибольшую высоту подъема тела.
а)3; б) 44,1 ; в)19,6; г) 68.
Найдите наибольшее и наименьшее значение функции в заданном промежутке, если у= х2 - х3; 1≤х≤3.
а)
-4,5 –наименьшее значение, ;
;
б)
-4 –наименьшее значение, ;
;
в)-13,5
–наименьшее значение, ;
;
г)0
–наименьшее значение, 22.
22.
2.Площадь осевого сечения цилиндра равна 81см2 . Найдите площадь полной поверхности цилиндра, если длина его образующей и длина диаметра основания равны.
а)324 ;
б)81
; в)18
г)36
;
б)81
; в)18
г)36
Найдите
функцию, дифференциал которой равен
(5х-2) зная,что
при х=2 функция принимает значение,
равное 20.
зная,что
при х=2 функция принимает значение,
равное 20.
а)y=
x3
+x2+4;
б)y
= 5 - 2x+14
; в)y
= 10x–
2; г)y
= 5x-2
- 2x+14
; в)y
= 10x–
2; г)y
= 5x-2
3.Найдите длину радиуса шара, равновеликого цилиндру радиуса 6см и высотой 3см.
Даны три вершины прямоугольника А(1;4;2;), В(2;-1;5), С(0;-2;4) прямоугольника АВСД. Найдите координаты вершины Д.
Диагонали ромба 12см и 16см. Точка М, расположенная вне плоскости ромба, удалена от всех сторон ромба на 8см. Определите расстояние от точки М до плоскости ромба.
а)2; б) -2 ; в)22; г) -22.
Составьте
уравнение линии, если угловой коэффициент
касательной в любой точке касания равен
 .
.
а)у =2; б)у =х+с; в)у = х; г) у=хс.
Ускорение движения тела, а= 24t2+8. Найдите закон движения тела, если в момент t=1с. Скорость тела v=10м/с, а путь равен12м.
а)s=8t3+8t- 6;б) s=8t3+8t+c; в)s=2t4+4t2+c г) s=2t4+4t2+6
Стороны основания прямоугольного параллелепипеда6см и 8см, а длина диагонали параллелепипеда равна 26см. Найдите высоту параллелепипеда и площадь диагонального сечения.
а)24см;240см2 б)28см,280см2 ; в)10см, 80см2; г)8см, 48см2.
Скорость движущегося тела равна v=(4t-t2)м/c. Вычислите путь пройденный телом от начала движения до остановки.
а)s=2t2
-
 +c;
б)10
в)
53
г)
3
+c;
б)10
в)
53
г)
3
Из некоторой точки пространства проведены к данной плоскости перпендикуляр, равный6см, и наклонная длиной 9см.Найдите длину проекции наклонной на данную плоскость.
а)3;
б) ; в)
; в) ; г)
; г) .
.
Скорость движущейся точки задана формулойv=2t-3(м/с).Найдите закон движения точки, если к моменту начала отсчета она прошла путь 6м.
а)s=2t3-3t- 6;б) s=2; в) s=2t2 - 3t+c г) s=t2– 3t +6
Найдите уравнение кривой, если угловой коэффициент касательной в каждой ее точке равен 2х.
а)у =2; б)у =х2+с; в)у = х2; г) у=хс.
