3. Перевірка гіпотези про істотність кореляційного зв’язку (строгий метод).

Кореляційний зв’язок вважають істотним, якщо довірчий інтервал для , обчислений з ризиком , не накриває нуль. Щоб побудувати довірчі межі для використовують, як правило, - перетворення Фішера (при ):

(5.8)

Для нашого прикладу маємо:

Довірчі межі будуємо для на основі відношення:

, (5.9)

де - квантиль, який вибирають із таблиці функції Лапласа (додаток 1) по значенню . Для нашого прикладу приймаємо , тоді . Із таблиць додатку 1 для значення , знаходимо, що . Значення обчислюють за формулою:

(5.10)

Для нашого прикладу (табл. 1): . Отже, . Довірчі межі для знаходимо по формулі (5.9):

(5.11)

Нижня межа для : .

Верхня межа : .

Тепер здійснюємо обернений перехід від до , які є границями для коефіцієнта кореляції за формулами:

, (5.12)

або за таблицею додатку 8. Для нашого прикладу маємо:

(по таблиці додатку 8 )

. Таким чином, для нашого прикладу довірчий інтервал для є наступним:

.

Якщо зобразити цей інтервал на осі , то бачимо з рис. 5 ,

Рис. 5. Довірчий інтервал для коефіцієнта кореляції .

що цей інтервал, на графіку він заштрихований, накриває нуль, а це значить, що на основі даної кількості спостережень істотність зв’язку не підтверджена, тобто, наявність зв’язку не доказана.

При обсязі пар більше 25 ( ) і нормальності генеральних сукупностей, зв’язок вважається встановленим, якщо:

, (5.13)

де обчислений за формулами (5.1) чи (5.7) коефіцієнт кореляції:

(5.14)

, - значення, яке вибирають із таблиці додатку 5 по значенням і .

4. Спрощений метод оцінки істотності коефіцієнта кореляції і його довірчого інтервалу.

Більш просто, але менш надійно, можна оцінити чи істотно обчисленій коефіцієнт відрізняється від нуля за допомогою табл. 2 яка містить критичні значення для випадку, коли істинній коефіцієнт кореляції = 0.

Наприклад, якщо вибірковій коефіцієнт кореляції = -0.844 (число тестованих студентів 10), то чи можна впевнено говорити про існування

взаємозв’язку, чи в дійсності кореляції нема, а отримане значення коефіцієнта обумовлено випадковостями вибірки?

Для того, щоб вирішити це питання, визначають спочатку число ступенів свободи для обчисленого нами за формулою:

,

де – число спостережень.

Вибираючи, як і раніше, рівень істотності знаходимо на перетині рядка для і колонки в табл.. 2 число . Вибіркове значення знаходиться значно дальше від нуля ніж критичне, тобто, кореляція між та дійсно існує. Границі для вибіркового коефіцієнта кореляції дані для рівнів значущості ; ; .

Таблиця 2

Число студентів свободи	Критичні значення коефіцієнта кореляції
2 3 4	0,900 0,805 0,729	0,950 0,878 0,811	0,990 0,959 0,917
5 6 7	0,669 0,662 0,582	0,754 0,707 0,666	0,874 0,834 0,798
8 9 10	0,549 0,521 0,497	0,632 0,602 0,576	0,765 0,735 0,708
20 30 50	0,360 0,296 0,231	0,423 0,349 0,273	0,537 0,449 0,354

Для швидкого, але наближеного визначення довірчих меж для визначеного нами вибіркового коефіцієнта кореляції , можна скористатись рис. 6. криві лінії на цьому рисунку обмежують довірчі границі для при різних обсягах вибірки. Ці обсяги вказані на рис. 2 по діагоналі з верхнього лівого до нижнього правого кута.

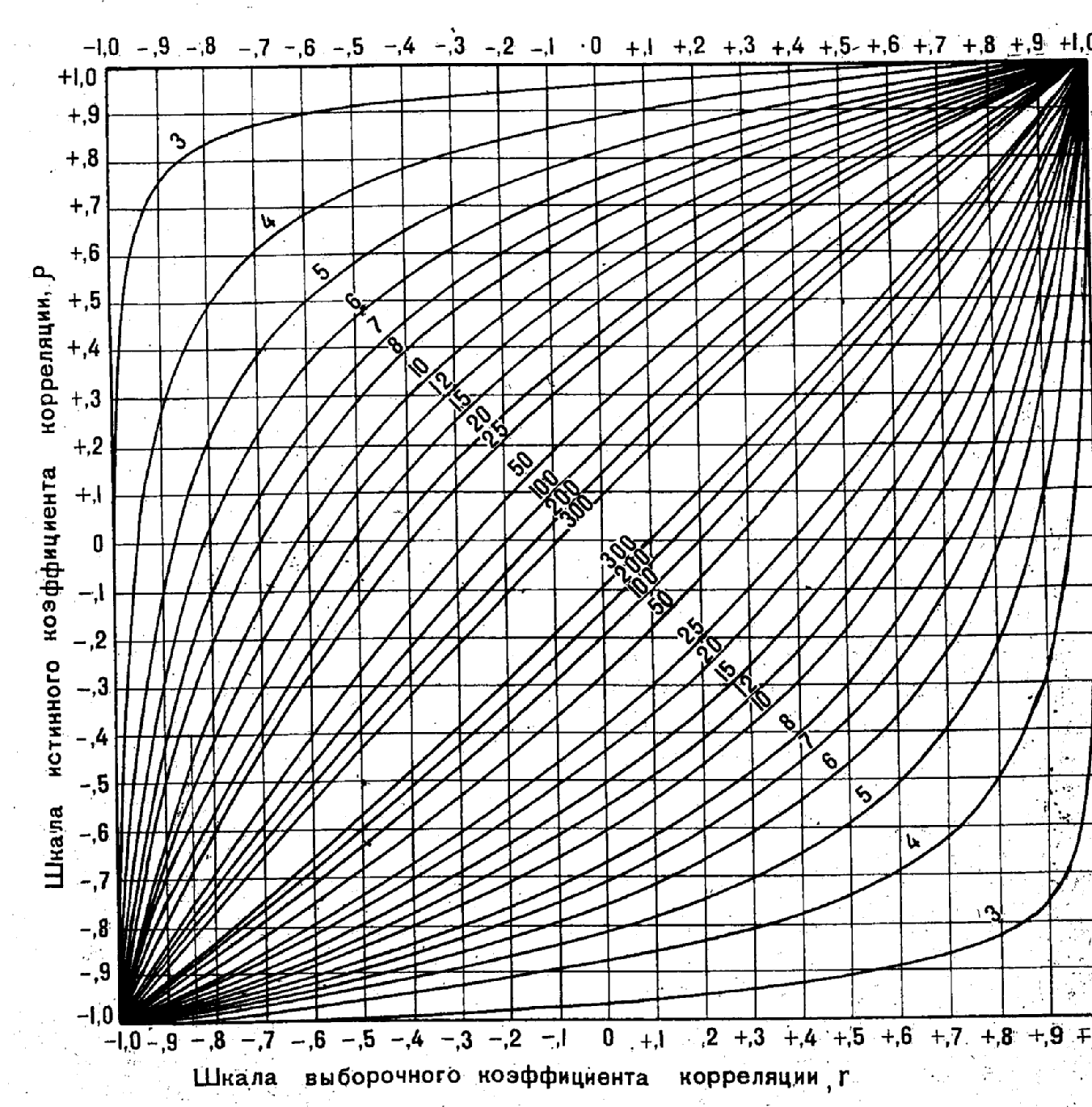
Рис.6. Графік для визначення довірчих меж вибіркового коефіцієнта кореляції для рівня значущості в залежності від обсягу вибірки.

Для того, щоб визначити довірчі межі для обчисленого нами (n = 10) проводимо вертикальну криву від точки вибіркового вверх, як показано на рис. 6. Ця вертикальна крива перетинає вриві обсягів для n = 10 в двох точках: -0.47 і -0.98: це і є граничні точки довірчого інтервалу. Отже довірчі межі для є наступними:

-0.98 < < -0.47

Як бачимо, ці довірчі межі приблизно відповідають точним межам, які знайдені нами раніше на основі z – перетворення Фішера.