Тема V Методи аналізу взаємозв’язків План

1. Види взаємозв’язків.

2. Кореляційний зв’язок, кореляційний аналіз, кореляційне поле, коефіцієнт кореляції.

3. Перевірка гіпотези про істотність кореляційного зв’язку на основі z-перетворення Фішера (строгий метод).

4. Спрощений метод оцінки істотності коефіцієнта кореляції і його довірчого інтервалу.

5. Непараметричний критерій Спірмена для оцінки сили кореляційного зв’язку.

6. Метод аналітичного групування і кореляційне відношення для оцінки взаємозв’язку при нелінійній формі залежності.

7. Кореляційно-регресійний аналіз лінійної залежності і коефіцієнт детермінації.

8. Дисперсійний аналіз і його суть.

9. Застосування однофакторного дисперсійного аналізу.

Базові поняття: факторна і результативна ознаки;функціональний і статистичний зв’язки;кореляційний зв’язок: прямий і обернений;коефіцієнт лінійної кореляції; призначення - перетворення Фішера; критерій Спірмена; емпірична лінія регресії; метод аналітичного групування; кореляційне відношення і його призначення; правило складання дисперсії; теоретична лінія регресії: лінійна та нелінійна; форма і параметри лінійної регресійної моделі і спосіб їх визначення; коефіцієнт детермінації і його призначення; дисперсійний аналіз і його суть.

Стислий огляд теми V.

1. Види взаємозв’язків.

Процеси фізичного виховання і фізичної реабілітації протікають не ізольовано, а під впливом різноманітних факторів і залежать, наприклад:

• від зацікавленості державних та інших структур у розвитку спорту;

• рівня матеріально-технічної бази підготовки спортсменів;

• частот міжнародних та національних змагань;

• масовості фізкультурно-оздоровчих та спортивних послуг;

• видів дефектів і аномалій, засобів їх корекції, тощо.

Тобто, будь-які результати у спорті чи фізичній реабілітації залежать і визначаються дією певного ряду основних і другорядних фактів. Ознаки, які характеризують причини та умови такої залежності називають факторними, а ті, які характеризують наслідки зв’язку – результативними. Вид зв’язку між факторною і результативною ознаками є різним. Наприклад, визначення прискорення по відомим даним швидкості в біомеханіці, закон Фехнера в психології, закон Хілла в фізіології характеризують так званий функціональний зв’язок, при якому кожному значенню факторної ознаки відповідає строго визначене значення результативної. До іншого виду взаємозв’язку відносять, наприклад, залежність ваги від росту спортсменам. Одному значенню росту може відповідати кілька значень ваги і навпаки. Отже, коли одному значенню факторної ознаки відповідає розподіл значень результативної, то такий взаємозв’язок є статистичним.

Вивченню статистичних залежностей між різними показниками в спортивних і реабілітаційних дослідженнях приділяють велику увагу, оскільки це дозволяє виявити найістотніші закономірності і описати їх математично з метою використання в практичній роботі тренера чи педагога.

2. Кореляційний зв’язок, кореляційний аналіз, кореляційне поле, коефіцієнт кореляції.

Серед статистичних залежностей найбільш важлива кореляційна (від лат. сorrelation - співвідношення). Кореляційним називають зв’язок, в якому кожному значенню факторної ознаки відповідає середнє значення результативної ознаки .

Статистичний метод, який використовують для дослідження взаємозв’язків називають кореляційним аналізом, основною метою якого є визначення форми, сили і напрямку зв’язку. Кореляційний аналіз (КА) дозволяє дослідити лише статистичний взаємозв’язок і широко використовується в спортивних дослідженнях в теорії тестів для оцінки їх інформативності і надійності. Різні шкали вимірів вимагають різних варіантів кореляційного аналізу.

КА починають з графічного представлення результатів вимірів в прямокутній системі координат. Допустим, що у 7 студентів, ми реєстрували такий показник як число підтягувань на перекладині на початку семестру ( - номер студента, ) і число підтягувань для них же в кінці семестру (табл. 1, колонки 1, 2, 3). Для цих результатів побудуємо графік, на осі абсцис якого відкладемо для кожного студента результат , а на осі ординат – результати .

Таблиця 1.

Номер студента			Розрахункові дані
1	10	12	120	100	144
2	9	13	117	81	169
3	12	12	144	144	144
4	10	11	110	100	121
5	11	13	143	121	169
6	11	12	132	121	144
7	10	14	140	100	196
8	10	13	130	100	169
9	12	11	132	144	121
10	11	10	110	121	100
Разом			1278

Рис.1 Кореляційне поле (діаграма розсіювання) і .

Таким чином в прямокутній системі координат кожна пара результатів (кожен студент) відобразиться точкою (рис. 1). Така графічна залежність називається кореляційним полем (діаграмою розсіювання) для залежності . Візуальний аналіз графіка є важливим етапом КА, оскільки він дозволяє виявити форму залежності. Якщо хмарка, точок близька до еліпсу, то кажуть, що між і існує лінійна форма залежності, або просто лінійна залежність.

Проте на практиці зустрічаються і інші форми залежності:

На рис.2 показана залежність між швидкістю тенісної ракетки і швидкістю вильоту м’яча . В цьому разі кореляційне поле (КП) нагадує нахилену букву „Г” (рис. 2).

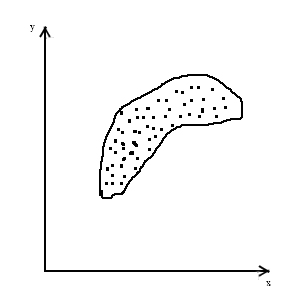
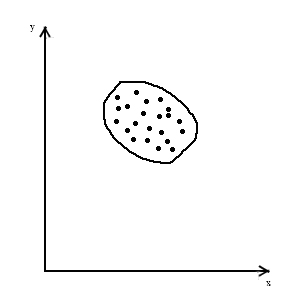
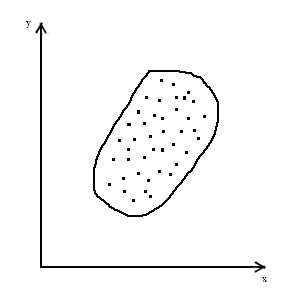
Рис.2. Кореляційне поле: Рис.3. Кореляційне поле Рис.4. Залежність між

резу льтатом

швидкість ракетки - у формі круга свідчить штовхання ядра 5 кг – вісь

швидкість м’яча про відсутність кореля- і 3 кг – вісь для групи

(нелінійна залежність) ційної залежності спортсменів

Така залежність, що експериментально отримана при подачах в тенісі, є видом нелінійного зв’язку. Візуальний аналіз КП дозволяє, також виявити відсутність зв’язку і його направленість (рис. 1 і рис. 4). На рис. 1 КП свідчить про обернений зв’язок: із збільшенням зменшується в цілому , а на рис. 4. КП ілюструє прямий характер зв’язку: із збільшенням , також збільшується .

Для оцінки тісноти і направленості зв’язку обчислюється спеціальний показник – коефіцієнт кореляції за формулою:

, (5.1)

де - середні прості для ; - число пар спостережень, - дисперсії показників .

Значення коефіцієнта кореляції може знаходитись в межах:

(5.2)

Формула (5.2) показує основну властивість коефіцієнта кореляції. Інтерпретують значення наступним чином: якщо , то кажуть, що зв’язок обернений; якщо , то зв’язок відсутній; якщо , то кажуть, що зв'язок прямий. Якщо , то кажуть, що зв’язок функціональний, відповідно прямий і обернений: в цьому разі значенню відповідає лише одне значення і тому ніякої варіації на КП не спостерігається. Далі, якщо:

, (5.3)

то це свідчить про дуже слабий статистичний зв’язок; якщо:

, (5.4)

то це є свідченням слабого статистичного взаємозв’язку; якщо:

, (5.5)

то кажуть, що між і є статистичний зв’язок середньої сили; якщо:

, (5.6)

то це свідчить про сильний статистичний взаємозв’язок.

Для обчислення коефіцієнта кореляції зручно скористатись такою формулою, яка ідентична наведеній вище:

(5.7)

За даними табл.1 маємо:

Як бачимо, зв’язок в даному є оберненим і слабим.