Тема ііі. Статистичні розподіли і їх характеристика. Показники варіації та форми розподілу. План

1. Статистичні розподіли і їх елементи.

2. Види статистичних розподілів. Їх графічне зображення.

3. Характеристики центру розподілу: середнє зважене, мода, медіана.

4. Характеристики варіації.

5. Моменти і характеристики форми розподілу: асиметрія і ексцес.

6. Пірсонівські характеристики форми розподілу і їх ідентифікація.

Базові поняття по темі ІІІ.

• ряд розподілу і його елементи: варіанти, частоти, кумулятивні частоти;

• атрибутивні і варіаційні (дискретні і неперервні) ряди розподілу;

• полігон і гістограма, комулята і огіва ряду розподілу;

• структурні середні: мода і медіана розподілу, квартилі;

• абсолютні характеристики варіації: розмах, середнє квадратичне відхилення, дисперсія, середнє лінійне відхилення;

• відносні характеристики варіації: квадратичний, лінійний, квартильний коефіцієнти варіації, коефіцієнт осциляції;

• моменти розподілу: початкові і центральні;

• характеристики форми розподілу: асиметрія і ексцес, пірсонівські характеристики форми розподілу .

Стислий огляд теми ііі.

Статистичний ряд розподілу – це впорядкований розподіл одиниць досліджуваної сукупності на групи по певній варіюючій ознаці.

Ряд розподілу складається з 2-х елементів: інтервалів або варіант – що являють собою значення групувальної ознаки і частот, які показують скільки спостережень попадає в інтервал (скільки раз повторюються задані значення варіантів). Частоти розподілу можуть заміняти інші його елементи: частки, кумулятивні частоти і кумулятивні частки, суть яких стає зрозумілою із табл. 1, де в колонці 2 дано варіанти, в колонці 3 – частоти, а в колонках 4 – 5, 6, 7 – 8 відповідно частки, кумулятивні частоти і кумулятивні частки .

Таблиця 1.

Розподіл результатів бігу 200 студентів на 100 м (хлопці)

№ і	Інтервали групува - ння (варіанти) сек.	Кількість студентів (частоти)	Частки		Кумулятив-ні частоти	Кумулятивні частки
				,%			,%
1	2	3	4	5	6	7	8
1	10,5 – 11,5	12	0,060	6,0	12	0,060	6,0
2	11,5 – 12,5	35	0,175	17,5	47	0,235	23,5
3	12,5 – 13,5	55	0,275	27,5	102	0,510	51,0
4	13,5 – 14,5	48	0,240	24,5	150	0,750	75,0
5	14,5 – 15,5	33	0,165	16,5	183	0,915	91,5
6	15,5 – 16,5	11	0,055	5,5	194	0,970	97,0
7	16,5 – 17,5	6	0,030	3,0	200	1,000	100,0
Разом			1,000	100,0	Х	Х	Х

В залежності від типу групувальної ознаки (атрибутивна чи кількісна) ряди розподілу поділяють на атрибутивні і варіаційні.

Атрибутивні – це такі розподіли, які побудовані по кількісній ознаці.

Варіаційними називають розподіли, що побудовані по кількісній ознаці. Вони поділяються на дискретні і інтервальні. Дискретними є ряди розподілу, що побудовані по дискретній ознаці (наприклад, розподіл жонатих спортсменів за кількістю дітей у сім’ї). Інтервальними є ряди розподілу, в яких значення групувальної ознаки задані у вигляді інтервалів (наприклад, в табл. 1).

Для наочного уявлення про характер зміни частот будуть полігон (для дискретних розподілів), гістограму (для інтервальних розподілів). Графік кумулятивних частот або часток називають кумулятою.

Центром тяжіння варіюючої ознаки розподілу є її типовий рівень, тобто

середня арифметична зважена (яку ми обчислюємо для даних табл.1):

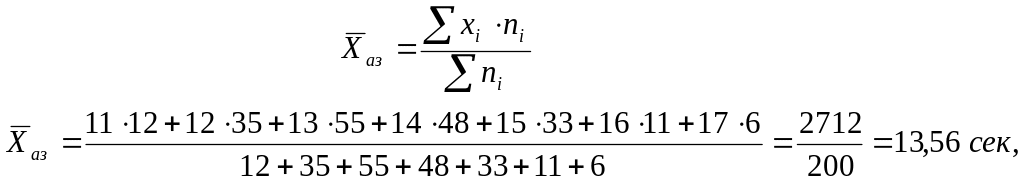
де - це номер інтервалу групування; - середнє значення ознаки в -тому інтервалі (середина інтервалу групування), - число спостережень в -тому інтервалі; ; - число інтервалів. Наприклад, в табл. 1 перший інтервал має , а частота .

Модою є таке значення ознаки, яка найчастіше повторюється. Для згрупованих даних мода обчислюється за формулою (за даними табл. 1):

де - нижня межа модального інтервалу.

Модальним є інтервал, який має найбільшу частоту , яка є модальною частотою; - відповідно частоти інтервалів, що знаходяться перед і після модального інтервалу; - ширина інтервалу групування.

Для незгрупованих даних медіаною є значення ознаки ранжированого ряду, яке ділить цей ряд на дві рівні половини за чисельністю. Для згрупованих даних медіану обчислюють за формулою (для даних табл. 1):

де - нижня межа медіанного інтервалу. Медіанним є інтервал, на який приходиться половина спостережень; - ширина інтервалу групування; - кумулятивна частота інтервалу, який передує медіанному. Кумулятивну частоту -го інтервалу обчислюють за формулою:

Квартилями незгрупованого ранжированого ряду є значення ознак, які відсікають включно частину спостережень. При цьому обсяг ряду має бути кратним чотирьом. До згрупованих даних вимога кратності не ставиться , а обчислюють за формулами (для даних табл. 1):

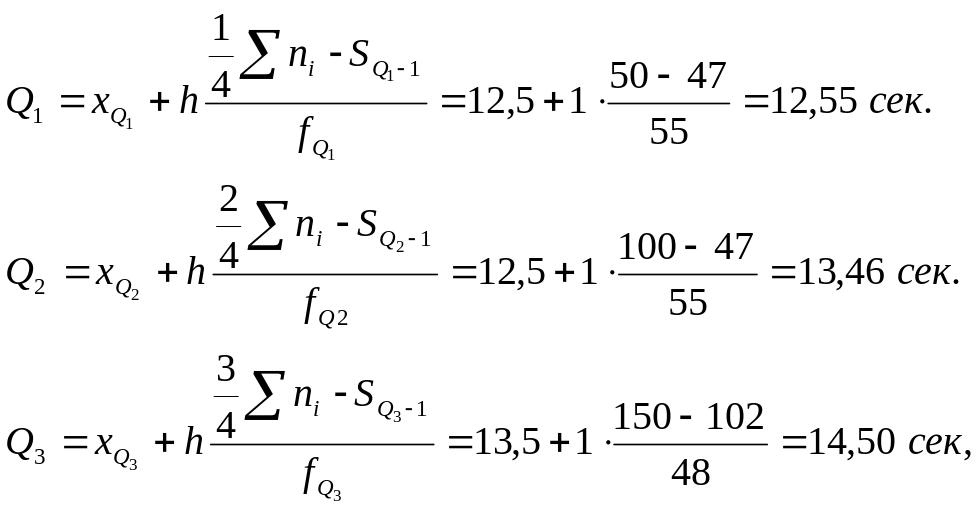
де - відповідно нижні межі першого, другого і третього квартильних інтервалів, які визначають по кумулятивним частотам, при цьому, перший квартильний інтервал - це інтервал на який припадає , другий - , третій - .

Розмах варіації для незгрупованих даних обчислюють за формулою: ,

де - максимальне і мінімальне значення ознаки в ряду спостережень.

Для згрупованих даних обчислюють як різницю крайніх значень розподілу, або як різницю центрів двох крайніх інтервалів розподілу. Розмах можна обчислювати двома згаданими способами, оскільки він є наближеною характеристикою. Наприклад, для даних табл.1

Середнє квадратичне відхилення просте , середнє лінійне відхилення просте обчислюють за формулами:

,

де - незгруповані результати спостережень; , - число всіх спостережень,

Середнє квадратичне відхилення зважене обчислюють за формулою (для даних табл.1):

Середнє лінійне відхилення зважене обчислюють так (за даними табл.1):

де - центр -го інтервалу групування; - число спостережень в -тому інтервалі; .

Дисперсія обчислюється за формулами:

Середнє квадратичне відхилення, середнє лінійне відхилення і дисперсія (прості і зважені), а також розмах – називають абсолютними характеристиками варіації. Відносні характеристики варіації обчислюють на основі абсолютних за наступними формулами:

• квадратичний коефіцієнт варіації:

;

• лінійний коефіцієнт варіації:

;

• коефіцієнт осциляції: ;

• квартильний коефіцієнт варіації:

Початковий момент порядку статистичного розподілу обчислюють за формулою:

.

Найважливішим із початкових моментів є .

Центральні моменти порядку обчислюють так:

.

Найважливішим із центральних моментів є .

Асиметрію , куртозис і ексцес розподілу обчислюють за формулами:

.

При розподіли мають лівосторонню асиметрію (лівий хвіст розподілу дуже довгий), при А>0 – правосторонню. При А=0 розподіл є симетричним.

При розподіл є плосковершинним, при - гостровершинним, при - нормальним.

В статистиці фізичного виховання і фізичної реабілітації можуть зустрітись найрізноманітніші розподіли, проте значення і дають лише приблизну уяву про форму розподілу. В той же час, як правило, потрібно знати математичну форму отриманого статистичного розподілу. Для визначення математичної форми розподілу, тобто для вирішення проблеми ідентифікації статистичного розподілу можна скористатись графіком, запропонованим К. Пірсоном (рис.), який дозволяє підібрати будь-яку математичну форму в системі кривих Пірсона в залежності від значень і .

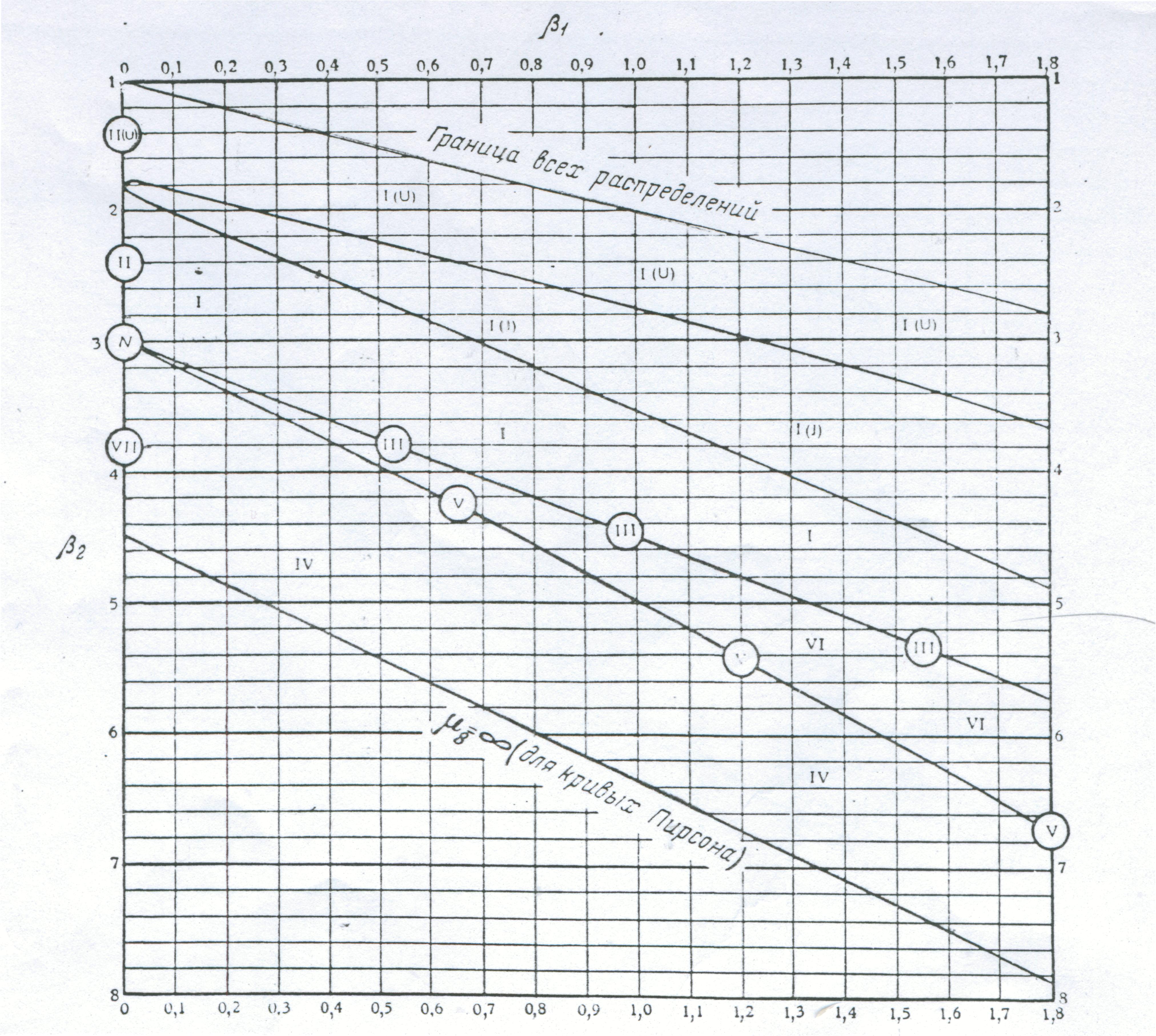
Рис. Графік для визначення математичної форми статистичного розподілу в системі кривих Пірсона.

Криві Пірсона є регулярними і охоплюють переважну більшість розподілів створених людством.

Якщо на графіку вказати точку з координатами , які обчислені для статистичного розподілу, то ця точка вкаже тип кривої Пірсона, яка може бути теоретичною формою розподілу досліджуваного явища. Наприклад, якщо точка з координатами попадає в окіл точки N, то це значить, що за теоретичну форму статистичного розподілу можна взяти нормальний закон, якщо в окіл лінії ІІ – то рівномірний розподіл і т.д.

Література: [2.8] с. 41-73; [1.4] с. 27-53

Тема ІV.

Вибірковий метод. Статистична перевірка гіпотез.

План

1. Основні поняття вибіркового методу.

2. Повторна і безповторна вибірки.

3. Точкова оцінка. Гранична похибка вибірки. Інтервальна оцінка.

4. Статистична гіпотеза і статистичний критерій.

5. Найуживаніші статичні критерії і їх застосування:

- - критерій (Пірсона);

- - критерій (Колмогорова);

- - критерій (Стьюдента);

- - критерій (Фішера).

Базові поняття по темі ІV

Поняття вибіркового методу. Генеральна і вибіркова сукупності. Похибки репрезентативності. Систематичні та випадкові похибки. Точкова оцінка. Гранична похибка вибірки. Повторна і безповторна вибірки. Статистична і наукова гіпотези. Статистичний критерій. Рівень істотності. Призначення критеріїв: Пірсона, Колмогорова, Стьюдента і Фішера.

Стислий огляд теми ІV

Вибірковий метод – є системою наукових принципів випадкового відбору певної частини сукупності, так, щоб ця частина репрезентувала всю сукупність і характеристики якої були б надійною основою статистичного висновку.

Рис. 1

Сукупність, з якої відбирають елементи для обстеження є генеральною, а сукупність, яку безпосередньо обстежують – вибірковою. (Рис.1) Статистичні характеристики вибіркової сукупності (ВС) називають статистиками, які розглядають як оцінки відповідних характеристик генеральної сукупності (ГС), які називають параметрами. Оскільки ВС не точно відтворює структуру ГС, то статистики також не збігаються з параметрами. Розбіжності між ними називають похибками репрезентативності. За причинами виникнення ці похибки поділяються на систематичні і випадкові. Систематичні похибки виникають внаслідок порушення принципу випадковості відбору або із-за неатестованих шкал вимірів. Випадкові похибки – наслідок випадковості відбору елементів сукупності для обстеження. Нехай - генеральне середнє, - вибіркове середнє, тоді дія виключно випадкових похибок буде визначати розподіл результатів навколо , рис. 2, а дія систематичних похибок означає зміщення центра розподілу , відносно на величину (рис.3).

x

Рис. 2. - область дії Рис. 3. - систематична похибка

випадкових похибок

При організації вибіркового спостереження важливо запобігти появі систематичних похибок, як найбільш небезпечних. Що стосується випадкових помилок, то уникнути їх неможливо, проте вибірковий метод дає строгий науковий метод їх оцінки. Так, відомо, що з імовірністю 0,997 випадкові похибки змінюються в межах , тобто в даному разі довірче число t=3. В межах випадкова похибка буде находитись з імовірністю 0,954, а в межах - з ймовірністю 0,683.

Існує два основних способи добору: повторний і безповторний. При повторному відборі елемент ГС навмання відбирають, фіксують його номер, потім повертають цей елемент назад у ГС. При повторному відборі той самий елемент може потрапити у ВС ще раз, оскільки склад ГС не змінюється.

Безповторним є добір, при якому відібрані елементи вибірки назад у ГС не повертаються.

Щоб забезпечити принцип випадковості відбору, як повторний так і безповторний відбір здійснюють з використанням таблиці (генератора) рівномірно розподілених випадкових чисел (додаток 10). Допустимо, що необхідно провести 10% відбір із групи 120 спортсменів з метою оцінки середнього рівня їх фізичної підготовки. Тоді, пронумерувавши всіх спортсменів, ми виписуємо 12 послідовних тризначних цифр менших 120 із таблиці додатку 10, тобто, це будуть номера: 100, 135, 63, 8, 166, 90, 15, 33, 190, 153, 131, 165. Аналогічно здійснюють безповторний відбір лише з тією різницею, що із номерів, які можуть двічі повторюватись, один закреслюють і добирають із таблиці наступний номер, але так, щоб число номерів у даній вибірці не перевищувало 12.

В практиці вибіркового методу використовують два типи вибіркових оцінок – точкові та інтервальні. Точкова оцінка – це оцінка параметра ГС за даними вибірки, наприклад, середнє по вибірці є вибірковою оцінкою параметра ГС. Для обчислення інтервальної оцінки потрібно знати граничну помилку вибірки , яка є максимально можливою похибкою для прийнятої імовірності . В даному разі довірче число вказує як співвідносяться гранична помилка і стандартна помилка вибірки .

Стандартна похибка вибірки обчислюється за формулою:

• при повторному відборі ;

• при безповторному ,

де - вибіркова дисперсія; – відповідно обсяги ВС і ГС.

При використанні наведених формул слід враховувати, що дисперсія частки:

,

де - частки певних елементів, а граничні похибки для частки в повторній і безповторній вибірках такі:

.

Отже, величини граничних похибок чи залежить від варіації чи , обсягу вибірки , та від , а також прийнятого рівня імовірності , якому відповідає квантиль . Квантиль – це число, яке є коренем рівняння , де - функція розподілу.

Інтервальна оцінка – це інтервал, що з певною імовірністю накриває шуканий параметр ГС і, яка розраховується на основі вибіркової оцінки цього ж параметра. Цей інтервал називають довірчим і його межі визначаються за формулами:

• для середньої: ,

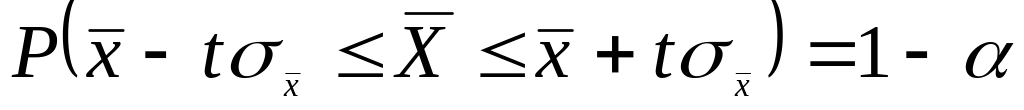• для частки: ,

де - рівень ризику, значення називають нижніми, а - верхніми межами довірчих інтервалів.

Статистична гіпотеза – це припущення щодо властивостей ГС чи її параметрів, яке перевіряють за даними вибірки. Наукова гіпотеза – це творчий акт, який пояснює виникнення явища, наприклад гіпотеза Лапласа про проходження Сонячної системи із велетенської хмари пилу.

Статистична гіпотеза, яку маємо перевірити, формулюється як відсутність розбіжностей між параметром ГС, наприклад і заданою величиною (нульова гіпотеза ). Зміст її записують так: . Кожній нульовій гіпотезі протистоїть альтернативна . Якщо вибіркові данні суперечать гіпотезі , вона відхиляється, якщо ні - приймається. Перевірка гіпотез неминуче пов’язана з ризиком помилкового рішення: помилка І роду – відхилення нульової гіпотези, коли насправді вона вірна і сформульована правильно; помилка ІІ роду – підтвердження невірної, неправильно сформульованої гіпотези. До найбільш небажаних наслідків приводять помилки ІІ роду, тому, при перевірці гіпотез, важливо правильно сформулювати .

Правило за яким приймають або відхиляють називають статистичним критерієм. Математичною основою будь-якого є статистична характеристика , закон розподілу якої відомий.

Ризик відхилення вірної (помилка І роду) називають рівнем істотності (рівнем ризику), а значення статистичної характеристики для імовірності - критичним значенням . У додатках 3-5 наведені критичні значення найпоширеніших статистичних критеріїв. Якщо вибіркове значення гіпотеза відхиляється при - приймається. У разі перевірки гіпотези проти використовують двосторонній критерій, критичне значення якого визначають для , тобто .

Критерій - Пірсона найчастіше використовують для перевірки узгодженості емпіричного розподілу з вибраним теоретичним розподілом. Якщо емпіричні частоти розподілу позначити через , то перевірка такої узгодженості зводиться до перевірки нерівності:

,

де - теоретичні частоти; - обчислюється за даними вибірки, а критичне значення вибирається із таблиці додатку 3 в залежності від і , - кількість стовпчиків (розрядів) емпіричного розподілу, - число параметрів теоретичного розподілу.

Критерій Колмогорова ( - критерій), у якому мірою розходження емпіричного і прийнятого теоретичного розподілу є максимальне значення модуля:

,

де відповідно кумулятивні частоти і значення теоретичної функції розподілу для відповідних інтервалів - число інтервалів (розрядів) розподілу. За значенням находиться величина , де - обсяг вибірки. Далі за значенням по таблиці додатку 4 знаходиться . Це і є імовірність того, що величина емпіричного розподілу дійсно відповідає закону . Якщо імовірність мала, то гіпотезу про узгодженість і відкидають як неправдоподібну; при великих - можна вважати, що емпіричний розподіл є адекватним теоретичному.

Критерій Колмогорова своєю простотою вигідно відрізняється від -критерію, тому його часто застосовують. Проте зауважимо, що його можна застосувати лише у тому випадку, коли гіпотетичний розподіл повністю відомий, тобто, коли відомий не лише вид функції , але і всі її параметри.

Критерій Стьюдента ( - критерій) використовують для перевірки істотності розходжень середніх: отриманих по двом вибіркам. Якщо результати спостережень в обох вибірках незалежні, рівноточні і нормально розподілені, то гіпотеза підтвердиться якщо буде мати місце нерівність:

,

де - обсяги першої і другої вибірок, - відповідно вибіркові дисперсії першої і другої вибірок; .

Значення вибирають із таблиць додатку 5 в залежності від . При цьому потрібно не забувати, що - критерій є двостороннім, тобто

Критерій Фішера ( - критерій) використовується для перевірки гіпотези , проти альтернативної гіпотези , де як і раніше відповідно вибіркові дисперсії обчислені по першій і по другій вибірках. Перевірка гіпотези зводиться до перевірки нерівності:

,

де - критичне значення -критерію, яке знаходиться по таблиці Фішера-Снедекора в залежності від значення трьох параметрів: (додаток 6). Якщо наведена нерівність для - відношення підтверджується, то приймається гіпотеза , якщо ні то приймається альтернативна гіпотеза

Література: [1.4] с. 54-57; [2.8] с. 95-99; [1.5] с. 129-150