Лабораторна робота № 2

Тема: Обчислення середніх величин і структурних середніх для згрупованих і незгрупованих даних.

Необхідно мати: конспект лекцій, методичні вказівки, калькулятор, лінійку.

План обчислень:

1. Середньої арифметичної і геометричної простих.

2. Середньої арифметичної зваженої.

3. Медіани для незгрупованих даних.

4. Моди і медіани для інтервальних розподілів.

Хід лабораторної роботи.

Перевірка готовності студентів до занять: усні відповіді студентів щодо суті середніх у статистиці – 5 хв.

1.1. Середню арифметичну просту обчислюємо за наступними результатами забігу 5 юнаків на 1500 м: .

Рішення: проводимо всі результати вимірів до однакової одиниці виміру, пам’ятаючи, що

Визначаємо обсяг ознаки: і визначаємо середню арифметичну просту за формулою: .

1.2. Середню геометричну просту обчислюємо для показників темпу зростання числа учасників масового забігу на 1000 м за 7 років.

Таблиця 2.1

Рік	1999	2000	2001	2002	2003	2004	2005
Число учасників забігу	105	90	110	128	130	121	140
Ланцюговий темп зростання числа учасників	-	0,857	1,222	1,164	1,016	0,931	1,157

Визначити середній темп зростання числа учасників за 6 років.

Рішення: Оскільки ланцюгові темпи зростання є відносними величинами, то для визначення середнього темпу зростання числа учасників забігу за 6 років, потрібно використати середню геометричну просту:

(2.2)

Отже, в середньому за 6 років число учасників масового забігу збільшувалось на 4,9 % в рік.

0. Обчислення середньої арифметичної зваженої:

Вихідними даними для вправи є результати групування концентрації альбуміну в крові для 70 жінок (табл. 1.2, лабораторна робота № 1). Середнє арифметичне зважене обчислюється лише за згрупованими даними по такій формулі:

(2.3)

де - середини інтервалів групування, а - число спостережень в -му інтервалі.

Обчислення по формулі (2.3) на основі даних таблиці даних 1.2 доцільно виконувати по формі таблиці 2.2.

Таблиця 2.2

Обчислення середньої арифметичної зваженої для статистичного розподілу концентрації альбуміну в крові 70 жінок-спортсменів

Інтервали розподілу	Середини інтервалів	Частоти
30-33	31,5	4	126,0
33-36	34,5	7	241,5
36-39	37,5	9	337,5
39-42	40,5	15	607,5
42-45	43,5	16	696,0
45-48	46,5	9	418,5
48-51	49,5	6	297,0
51-54	52,5	3	157,5
54-57	55,5	1	55,5

Отже, за формулою (2.3) і даними таблиці (2.2) середнє арифметична зважена для концентрації альбуміну в крові є наступною:

г/л .

0. Медіану обчислюємо для двох рядів незгрупованих даних, а саме, для результатів забігу на 100 м.

5 юнаків і 6 дівчат:

Юнаки: 13,5; 14,0; 13,2; 14,5; 14,3.

Дівчата: 17,1; 16,5; 17,4; 16,8; 17,2; 16,9.

Рішення: Ранжируємо перші і другі ряди спостережень:

Юнаки: 13,2; 13,5; 14,0; 14,3; 14,5.

Дівчата: 16,5; 16,8; 16,9; 17,1; 17,2; 17,4.

В першому ряду (юнаки) , оскільки це значення ділить ранжирований ряд на дві рівні половини за чисельністю. Для другого ряду (дівчата) :

.

4.1. Для обчислення моди інтервального ряду скористаємось даними табл.1.2 в лабораторній роботі № 1. В цій таблиці найбільшу частоту має інтервал 42-45. Отже, цей інтервал є модальним і його нижня межа . Скориставшись формулою для обчислення моди, маємо:

г/л .

4.2. Обчислення медіани виконаємо для того ж розподілу за формулою:

.

Пам’ятаючи, що і, що в п’ятій колонці таблиці 1.2 лабораторної роботи № 1 це число попадає на інтервал 39-42, визначаємо нижню межу медіанного інтервалу: г/л, отже,

г/л .

Висновок: структурні середні статистичного розподілу концентрації альбуміну у крові жінок є наступними:

Це означає, що найбільш часто у досліджуваних жінок-спортсменів концентрація альбуміну досягає 42,4 г/л, а концентрація г/л є ознакою, яка ділить розподіл рівно на дві половини за чисельністю.

Лабораторна робота № 3

Тема: Обчислення характеристик варіації для незгрупованих і згрупованих даних.

План.

1. Контроль готовності студентів до заняття.

2. Обчислення абсолютних і відносних характеристик варіації для незгрупованих даних.

3. Обчислення абсолютних характеристик варіації для згрупованих даних.

4. Обчислення кварталів для згрупованих даних.

Домашнє завдання:

1. Обчислення відносних характеристик варіації для згрупованих даних.

Хід лабораторної роботи.

1. Обчислення абсолютних характеристик варіації для незгрупованих даних за наступними даними (табл. 3.1).

Таблиця 3.1

Показники часу реакції в мілісекундах для чотирьох мотогонщиків

Прізвище спортсмена	Самородов	Цибров	Чапало	Чекушев
(ЧР), Час реакції	181+N	190	185	205-N

Рішення: для нульового варіанта маємо:

0. Розмах варіації ЧР: мс.

1. Середнє лінійне відхилення: 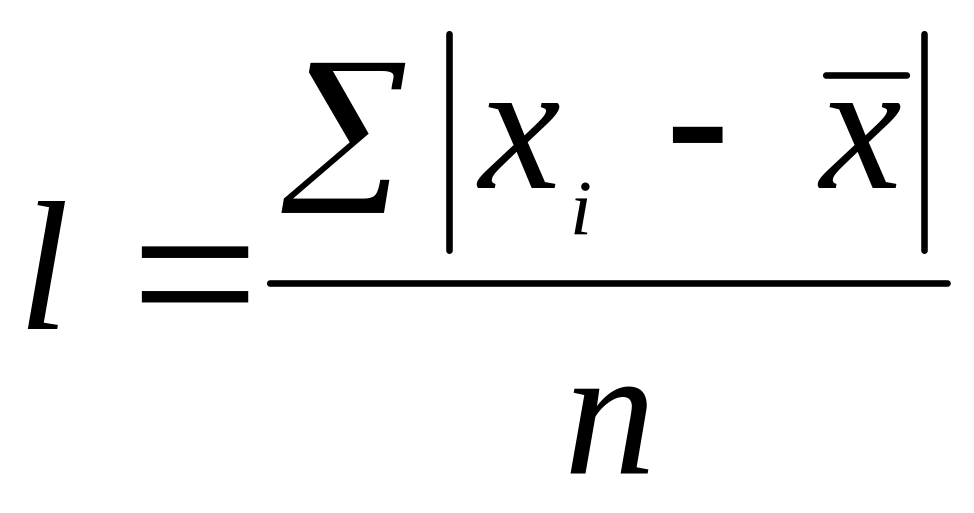; мс.

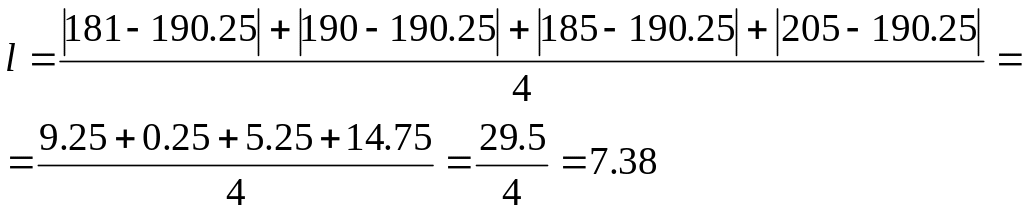
0. Дисперсія показників ЧР:

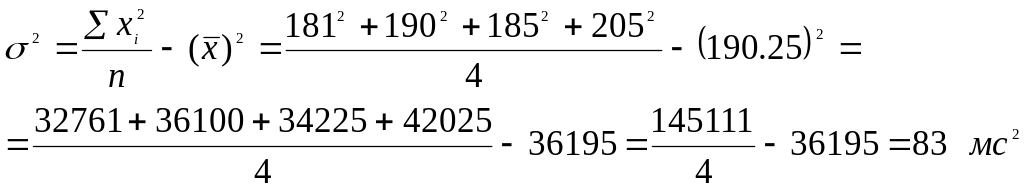
1.4. Середнє квадратичне відхилення: . Отже, значення абсолютних характеристик варіації ЧР для чотирьох спортсменів мотогонщиків є наступними:

.

2. Обчислення відносних характеристик варіації для незгрупованих даних здійснюють на основі обчислених абсолютних.

2.1. Квадратичний коефіцієнт варіації:

;

2.2. Лінійний коефіцієнт варіації:

.

2.3. Квартильний коефіцієнт варіації . Для знаходження медіани і квартилів ранжируємо ряд вихідних даних табл. 3.1:

181,\ 185,\ 190,\ 205

Таким чином Квартилі: отже,

2.4. Коефіцієнт осциляції .

Висновок: значення відносних характеристик варіації для даних табл. 3.1 є наступними:

3. Обчислення абсолютних характеристик варіації для згрупованих даних на основі табл. 1.2 (лабораторна робота №1.).

Обчислення доцільно вести по формі табл. 3.2.

Таблиця 3.2.

Розрахунки для обчислення абсолютних характеристик варіації по згрупованим даним.

Середини інтервалів,	Частоти,
1	2	3	4	5	6
31,5	4	-10,5	-42,0	42,0	441,0
34,5	7	-7,5	-52,5	52,5	393,8
37,5	9	-4,5	-40,5	40,5	182,2
40,5	15	-1,5	-22,5	22,5	33,8
43,5	16	1,5	24,0	24,0	36,0
46,5	9	4,5	40,5	40,5	182,2
49,5	6	7,5	45,0	45,0	337,5
52,5	3	10,5	31,5	31,5	330,8
55,5	1	13,5	13,5	13,5	182,2
Разом	70		-157,5 154,5	311,5	21195

3.1. Обчислюємо розмах варіації за даними колонки 2 табл. 3.2

г/л

3.2. Обчислюємо середнє лінійне відхилення . Значення ,обчислено в п. 2.1. лабораторної роботи № 2 .

3.3. Дисперсія .

3.4. Середнє квадратичне відхилення . Отже, абсолютні характеристики варіації для згрупованих даних табл. 3.2 є наступними:

4. Обчислення відносних характеристик варіації для згрупованих даних на основі абсолютних.

4.1. Квадратичний коефіцієнт варіації:

.

4.2. Лінійний коефіцієнт варіації:

4.3. Квартальний коефіцієнт варіації: . Медіана визначена в лабораторній роботі № 2.

Квартилі визначаємо користуючись колонками 1, 2 і 5 табл.1.2 пам’ятаючи при знаходженні квартильних інтервалів, що . Отже,

.

.

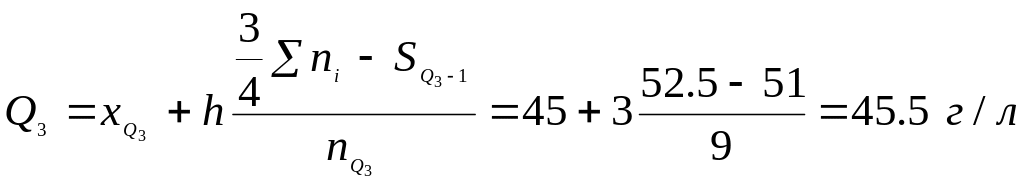
4.4. Коефіцієнт осциляції . Висновок: відносні характеристики варіації для концентрації альбуміну в крові 70 жінок є наступними: .