7. Кореляційно – регресійний аналіз лінійної залежності і коефіцієнт детермінації.

В практичних дослідженнях часто виникає необхідність описати кореляційне поле математичним рівнянням.

Для лінійної залежності це зробити просто: кореляційний еліпс заміняють прямою:

, (5.21)

яка називається рівнянням регресії. Коефіцієнти і називаються параметрами рівняння регресії, - значення визначає відрізок, який відсікає пряма на осі , - це тангенс кута нахилу прямої до осі .

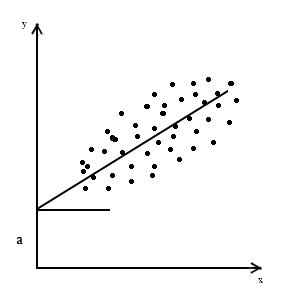
Рис. 8. Стрілкою показана пряма, яка є рівнянням регресії.

Для визначення параметрів рівняння регресії застосовують формули:

; ; (5.22)

де ; ; (5.23)

– коефіцієнт кореляції

; . (5.24)

Скористаємось даними табл.1 і визначимо параметри прямої регресії (5.21) для кореляційного поля, яке зображено на рис. 8

Скориставшись формулами (5.23) і (5.24) і даними нижнього рядка табл.2 маємо

Коефіцієнт кореляції, обчислений для даних табл.1, беремо з формули 5.7а:

= -0.442

= =1.136

= =0.916

= -0.442 =-0.548

Таким чином, рівняння регресії , для даних табл.1, має такий вигляд:

(5,24)

Для оцінки істотності зв’язку, тобто для підтвердження того, що формула (5.24) дійсно відображає реальній зв’язок, знаходять нерівність

, (5.25)

де - коефіцієнт детермінації, який обчислюють за формулою:

, (5.26)

- факторна дисперсія, яку обчислюють так:

(5.27)

- загальна дисперсія, яку обчислюють за формулою:

(5.28)

Значення в формулі (5.25) називають критичним значенням коефіцієнта детермінації, яке вибирають з таблиці додатку 7 в залежності від рівня значущості і ступенів вільності:

, (5.29)

де – число параметрів рівняння регресії (5.21).

Оцінимо істотність рівняння зв’язку (5.24), скориставшись формулами (5.25) – (5.29) і даними нижнього рядка табл.1.

Отже,

;

Обчислення залишкової дисперсії проведемо в табл.3, використовуючи значення і табл.1. Отже

Таблиця 3

№ п/п
1 2 3	10 9 12	12 13 12	12,43 12,98 11,33	-0,43 +0,02 +0,67
4 5 6	10 11 11	11 13 12	12,43 11,88 11,88	-1,43 +1,12 +0,12
7 8 9 10	10 10 12 11	14 13 11 10	12,43 12,43 11,33 11,88	+1,57 +0,57 -0,33 -1,88
			Х	-4,07 +4,07

Контроль правильності обчислень , здійснюють на основі правила складання дисперсій:

1,29=0,267+1,038

1,29=1,305 (5.30)

Отже, розходження правої і лівої частини в (5.30) знаходиться в межах точності обчислень, а це значить, що і вирахувані правильно і можна знаходити коефіцієнт детермінації

Критичне значення коефіцієнта детермінації знаходимо з таблиці додатку 7 в залежності від

Як бачимо

Таким чином:

Тобто, нерівність (5.25) не виконується, а це значить, лінія регресії не відображає істотний зв’язок, іншими словами – лінія регресії зображає недоказаний зв’язок.