11. Принципы широкополосного согласования сопротивлений

Устройства, рассмотренные выше, обеспечивают точное согласование только на одной (выбранной) частоте  . Задавшись некоторым допустимым рассогласованием _доп, мы получим полосу 2, в которой ||_доп. Ширина ее будет тем меньше, чем сильнее z_н отклоняется от w.

Построение широкополосной согласующей цепи – непростая задача. Мы здесь ограничимся только случаем чисто активной нагрузки. Согласование комплексной нагрузки – это отдельная задача, мы ее касаться не будем.

Итак, пусть z_н=R и не зависит от частоты. В частности, к этому случаю сводится задача построения согласующего перехода от линии с волновым сопротивлением w₀ к линии с другим сопротивлением w=R. Требуемыми свойствами обладает идеальный трансформатор с коэффициентом трансформации . Однако создать реальный трансформатор (на катушке с ферромагнитным сердечником), близкий по свойствам к идеальному, можно только в диапазоне НЧ. На ВЧ и особенно СВЧ подобное устройство нереализуемо и здесь применяют совершенно иные технические решения.

1) Многосекционный четвертьволновый трансформатор. Это – несколько каскадно включенных отрезков с разными волновыми сопротивлениями, длина каждого отрезка l=_ /4, где _ соответствует центральной рабочей частоте.

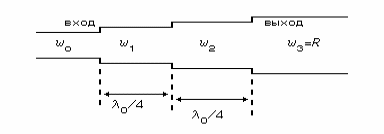
Обозначим – коэффициент трансформации (не обязательно целое число!), m – число _/4-секций, w_k – волновое сопротивление k-ой секции. Общая длина перехода равна

.

На стыке двух секций образуются ступенька – скачок волнового сопротивления. Если на k-ю ступеньку слева падает волна, то она частично отражается и частично проходит дальше, причем

1–|_k|² =|S_k|² – коэффициент прохождения.

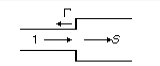
Местный коэффициент отражения равен

Допустим, что w_k и w_k–1 мало отличаются, тогда |_k|<<1, а |_k|² имеет второй порядок малости, поэтому приближенно можно считать |S_k|=1, а также пренебречь вторичными отражениями от ступенек. В этом приближении общий коэффициент отражения равен сумме местных коэффициентов отражения (пересчитанных ко входу с учетом фазовых задержек):

(1)

Отражения от ступенек суммируются на входе в разных фазах и в значительной степени взаимно компенсируются. Подбором коэффициентов _k можно добиться оптимальной формы характеристики рассогласования |(j)| в заданной полосе частот. Форма характеристики зависит от относительных значений _k, а абсолютные значения _k зависят от n. Можем записать (обозначив R=w_m+1)

, причем .

Логарифмируя с учетом малости |_k|, получим

. (2)

Сама характеристика (1) является полиномом m-ой степени

, (1а)

где играет роль обобщенной частотной переменной, так как

Для m=1 (простейший /4-трансформатор) имеем

из (2)

откуда

Но .

Пусть для определенности n>1. Тогда

, вблизи _ .

Чем больше n, тем уже полоса, в которой ||<_доп

Для m=2 выберем коэффициенты в соотношении _:_:_ =1:2:1, тогда

,

Вблизи _:

.

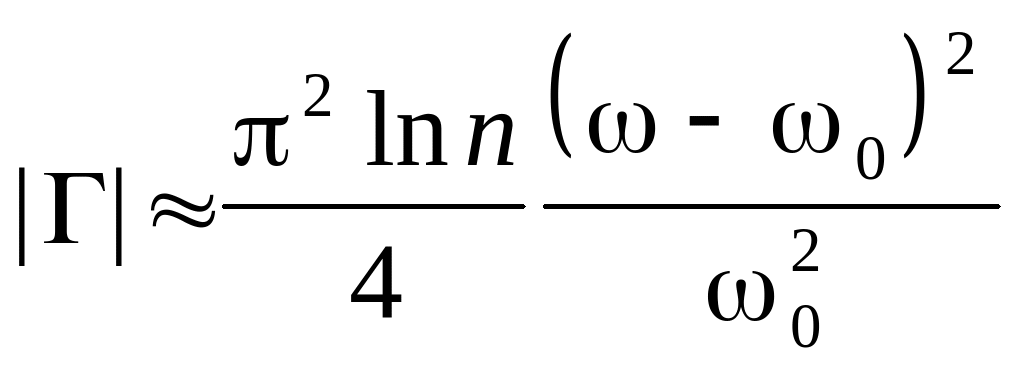Характеристика имеет параболическую форму, полоса частот значительно расширяется. Заметим, что более точная теория приводит к такому же результату, только lnn в выражении для  заменяется на , а соотношения между w_k сохраняются. Для сравнения 2-секционного трансформатора с односекционным в таблице 1 приведены значения относительной полосы частот /_ при _доп =0,1.

Таблица 1

n или 1/n	2,0	4,0
m=1	17%	7%
m=2	47%	30%

Увеличивая число секций m, можно еще более расширить полосу частот или уменьшить _доп в заданной полосе частот. Потому что скачки w_k /w_k-1 между соседними секциями с ростом m уменьшаются, уменьшаются и коэффициенты _ , а взаимная компенсация отражений с увеличением числа слагаемых в (1) улучшается.

Чаще всего применяют два варианта выбора относительных значений _k. В первом (пропорционально биномиальным коэффициентам). Тогда  описывается биномом m-ой степени

=₁(1+)^m , что дает

– (уточненная формула). Характеристика имеет форму параболы m-ой степени и называется максимально плоской (или характеристикой Баттерворта). Во втором случае w_k подбираются так, что характеристика описывается полиномом Чебышева m-ой степени. Чебышевская характеристика в рабочей полосе частот имеют пульсации между 0 и _доп . Длина такого перехода меньше, чем в первом варианте при одинаковых n и полосе частот. Есть справочники по расчету параметров переходов.

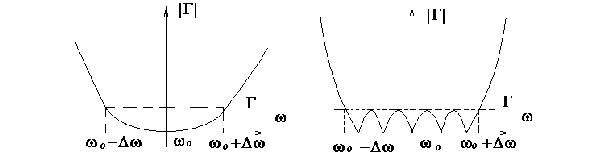
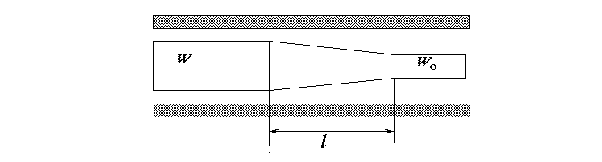
Конструкция коаксиального двухсекционного согласующего трансформатора показана на рис .

2) Плавный трансформатор. В этом устройстве w меняется вдоль линии не скачком, а непрерывно. Т.е. трансформатор представляет собой отрезок неоднородной линии, ее погонные параметры L и C зависят от координат. Дифференциальные уравнения такой линии имеют переменные коэффициенты. В общем случае они не поддаются точному аналитическому решению, приходится использовать приближенные или численные методы.

Рассмотрим частный случай неоднородной экспоненциальной линии, для которой

.

Обозначим x будем отсчитывать от конца линии. После подстановки L(x), C(x) в телеграфные уравнения, получим

или

В результате сокращения на множитель e^2x уравнение имеет постоянные коэффициенты, что позволяет решить задачу точно.

Характеристическое уравнение ² +2+^ =0 имеет корни

, где обозначено .

Решение для U будет

(3)

Ток I находится дифференцированием:

Преобразуем выражение

Обозначим и учтем, что

Тогда получим

и подставим это в I(x):

(4)

Найденные решения (3,4) показывают, что в линии распространяются волны противоположных направлений, причем амплитуда напряжения обеих волн при >0 убывает к началу линии, а амплитуда тока растет в такой же степени (при <0 картина обратная). Происходит трансформация напряжения и тока без изменения передаваемой мощности.

Фазовая постоянная обеих волн b=cos<. Следовательно, фазовая скорость больше, чем в однородной линии:

и зависит от частоты (то есть имеет место дисперсия.

Между напряжением и током падающей волны имеется сдвиг фаз , зависящий от , то же можно сказать и об отраженной волне.

На НЧ становится <||, процесс утрачивает волновой характер.

Найдем входное сопротивление в сечении x:

, где p=B/A

Коэффициент отражения в сечении x определим как

Пусть конец линии нагружен на w₀, тогда (0)=0, откуда находим

В начале линии окончательно получим

(5)

Хотя в линия на конце согласована, ее входное сопротивление отличается от w(l). Полное согласование наблюдается только при l=m, m=1,2,... (когда l кратно /4). На остальных частотах будет рассогласование, тем большее, чем больше ||/.

Рассмотрим подробнее частотную зависимость ||, приняв для определенности, что a>0. Введем, как и прежде, коэффициент трансформации перехода

, тогда

В области l>>.lnn(т.е.a<<) можно положить b=, модуль знаменателя в (5)1, тогда получим

Если же l0, то в пределе приходим к скачку сопротивлений w₀/w(l)=n² , следовательно,

Как мы видим, с ростом частоты согласование улучшается, т.е. полоса пропускания сверху теоретически неограниченна.

При =const согласование улучшается с ростом l Для обеспечения ||0,1 длина трансформатора должна составлять l_т_max, если n=2; и l_т2_max,, если n=4.

Экспоненциальный переход далеко не оптимален среди плавных переходов. Используя иной закон w(x), можно вдвое и более уменьшить длину при том же уровне _доп. В справочной литературе имеются формулы, графики и таблицы для расчета плавных переходов различных видов (в том числе с чебышевскими и максимально плоскими характеристиками).

Отметим, что при оптимальной характеристике согласования плавный переход получается длиннее ступенчатого из-за избыточности по полосе (поскольку последний является полосовым фильтром, а плавный - фильтром ВЧ).