8. Коэффициент передачи и коэффициент полезного действия отрезка длинной линии

В сечении l:

.

Отсюда находим активную мощность, переносимую через сечение l (считая w вещественным)

Но , поэтому

В РБВ , что позволяет трактовать данную величину как мощность падающей волны P_1пад.

С увеличением || передаваемая мощность уменьшается (если P_пад =const). При ||=1 мощность не передается.

Мощность, потребляемая нагрузкой, равна

, причем .

КПД отрезка линии можно определить как отношение

Часто используют несколько иное определение:

.

В обоих случаях КПД максимален при отсутствии отражений (РБВ):

.

Рассогласование линии не только снижает КПД, но и приводит к увеличению напряжения и тока (в пучности) при заданной мощности в нагрузке (они увеличиваются в раз по сравнению с РБВ).

Дело, однако, не только и не столько в мощности и КПД. Рассмотрим коэффициент передачи отрезка линии по напряжению, т.е. передаточную функцию (потерями пренебрегаем)

Видно, что при больших l K(j) резко зависит от частоты: АЧХ имеет изрезанный вид (относительный размах колебаний равен KCB ), ФЧХ тоже имеет сильную неравномерность. Следовательно рассогласование вызывает искажение формы передаваемого сигнала. Искажение проявляется в наложении на сигнал многократного эха, возникающего вследствие переотражений между нагрузкой и источником сигнала.

10. Простейшие методы согласования линии с нагрузкой

Выше говорилось о том, насколько важно обеспечить в линии РБВ. Однако в реальной ситуации z_н очень часто отличается от w линии, Тогда приходится применять специальные меры по согласованию линии с нагрузкой.

Согласующая цепь в общем случае представляет собой реактивный двухполюсник, включенный перед нагрузкой и трансформирующий ее сопротивление в величину z_вх =w. Тем самым она обеспечивает в линии РБВ и при этом не вносит дополнительных потерь.

Рассмотрим простейшие согласующие цепи.

1)Четвертьволновый трансформатор. Входное сопротивление /4-отрезка линии равно z(/4)=w²/z_н . Это трансформирующее свойство /4-отрезка и используется в согласующей цепях.

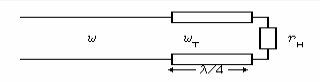
а) Если z_н =r_н (вещественное), то между линией и нагрузкой включается отрезок длиной  /4 (на центральной рабочей частоте) с другим волновым сопротивлением, которое берется равным , тогда на входе отрезка

т.е. питающая линия будет согласована.

б) Если z_н комплексное, то /4-трансформатор подключается не прямо к z_н , а в таком сечении l₁ , где |U| максимально или минимально и, следовательно, z(l₁)=r вещественно. Длину l₁ и величину r легко найти с помощью круговой диаграммы. После этого задача сводится к предыдущей: .

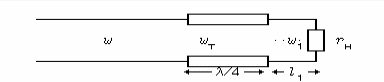
в) Еще один вариант при комплексной z_н =1/y_н : реактивная часть проводимости jb_н компенсируется проводимостью jb_ш замкнутого или разомкнутого на конце отрезка линии (b_ш = –b_н ), а /4-трансформатор подключается непосредственно к нагрузке ).

2) Реактивный шлейф (одно-шлейфный трансформатор). Этот способ удобен тем, что не нужно нарушать целостность соединения линии с нагрузкой. Необходимо отыскать такое сечение l₁, в котором относительная входная проводимость равна Y(l₁)=1+jB (такое сечение всегда существует, желательно выбрать наиболее близкое к нагрузке). В этом сечении параллельно линии подключается отрезок другой линии (шлейф), замкнутый или разомкнутый на конце.

Длина шлейфа l_ш выбирается так, чтобы его проводимость равнялась jb_ш = –jb₁ (абсолютные проводимости, если w_шw). Тогда суммарная входная проводимость соединения будет равна y_вх =1/w, т.е. вся оставшаяся часть входной линии будет согласована.

Расчеты величин l₁ и l_ш удобно выполнять на круговой диаграмме. Окончательную точную настройку производят, перемещая шлейф вдоль линии и изменяя его длину. В коаксиальных и двухпроводных конструкциях l_ш изменяют путем перемещения КЗ перемычки (поршня), а в полосковых удобнее разомкнутый на конце шлейф.

3) Двухшлейфный трансформатор. Применяется в случаях, когда неудобно менять место подключения шлейфа (например, в коаксиальной линии).

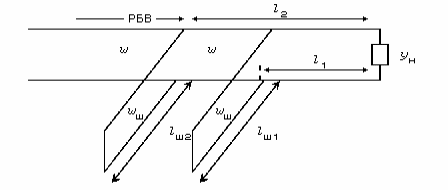
Здесь две степени свободы: l_ш1 и l_ш2 , а l₂ и l₁ фиксированы. Вначале путем вариации длины l_ш1 нужно достигнуть того, чтобы G(l₂)=1, что возможно не при любых сочетаниях l₁, l₂ и Y(l₁) . Если это удалось, то остается скомпенсировать B(l₂) вторым шлейфом, что уже возможно всегда.

Как выбрать расстояние l=l₂ –l₁? Пусть Y=G+jB –относительная проводимость в сечении l₁ вместе со шлейфом Ш₁ . Этот шлейф влияет только на B, но не влияет на G. Далее имеем

Если , тем больше G, но растут потери из-за больших реактивных токов и повышаются требования к точности. Это объясняется тем, что вследствие tgl<<1 будет B>>1, т.е. ток шлейфа значительно больше тока нагрузки. При этом шлейф близок к последовательному резонансу, и малое изменение его длины может приводить к резкому (в несколько раз) изменению B . Отсюда потери, критичность настройки и узкополосность. Поэтому берут l=/8, тогда можно согласовать при G2 (заштрихована область G>2).

Легко видеть, что с помощью трех шлейфов, размещенных на расстоянии l=/8 друг от друга, можно согласовать любую нагрузку. Действительно, если G<2, то используют только Ш₁ и Ш₂ , а длину третьего берут l₃ =/4. Если же G>2, то делают l₁=/4, тогда Y(l₂) будет в области внутри пунктирной линии и ее можно Ш₂ и Ш₃.

Недостаток всех рассмотренных способов согласования - узкополосность.