4. Уравнения передачи длинной линии. Коэффициент отражения.

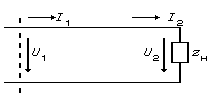
В общем случае в линии присутствуют волны обоих направлений

Обычно волну, распространяющуюся к нагрузке, называют падающей, а волну обратного направления – отраженной. Можно написать

, откуда .

Напряжение и ток в сечении, отстоящем на расстоянии l от нагрузки, равны

.

Заметим, что в любом сечении I_пад =U_пад/w, I_отр = –U_отр/w.

Полученные соотношения можно записать еще так

.

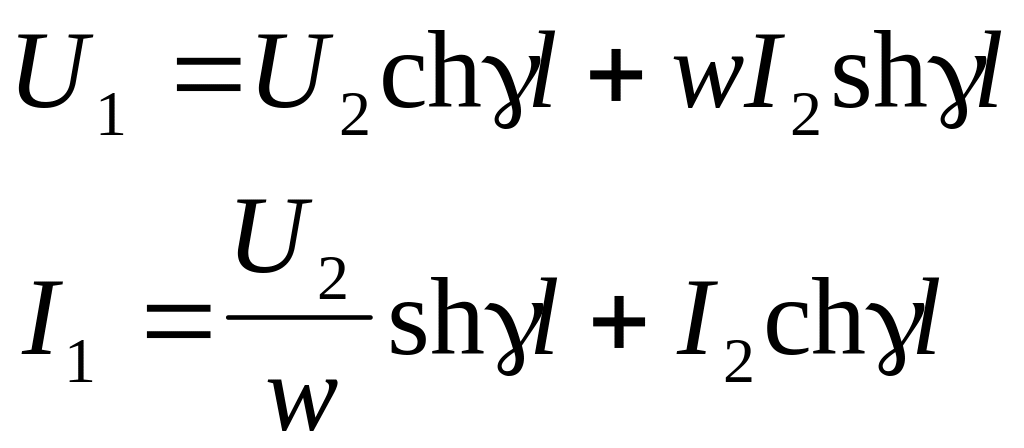Это – уравнения передачи отрезка линии произвольной длины, они имеют форму соответствующих уравнений четырехполюсника. Коэффициенты уравнений образуют матрицу передачи.

Подчеркнем, что U₁, I₁ относятся к любому сечению линии на расстоянии l от нагрузки (необязательно к началу всей линии). Нагрузка тоже не обязательно сосредоточенная (ею может быть тоже линия).

Введем важное понятие коэффициента отражения (по напряжению) как отношение (комплексных) напряжений отраженной и падающей волн:

– коэффициент отражения в сечении l (отсчет от нагрузки!), где

– коэффициент отражения в месте подключения нагрузки.

Учитывая, что U₂=z_нI₂, получаем

.

В сечении l от нагрузки

С увеличением l модуль  уменьшается, а сам вектор  поворачивается на угол –2l.

Аналогичный коэффициент отражения по току отличается от  лишь знаком

,

и его обычно не используют.

Некоторые частные случаи.

1. z_н =w, тогда (0)=0, следовательно, (l)=0, т.е. РБВ. В этом случае говорят, что линия согласована с нагрузкой.

2. z_н = (режим холостого хода): (0)=1.

3. z_н =0 (режим короткого замыкания): (0)= –1.

4. z_н =jx_н (реактивная нагрузка):

,

и, если Im w=0 (что практически имеет место на ВЧ и СВЧ), |(0)|=1.

В трех последних случаях |(0)|=1, т.е. происходит полное отражение волны от нагрузки. По мере удаления от нагрузки будет уже |(0)|<1 вследствие затухания.

5. Волны в линии без потерь

Обычно на ВЧ затухание в линии относительно мало: << и заметно сказывается только при передаче на значительные расстояния (l>>). Если же l одного порядка с , то потерями вполне можно пренебречь, положив =0.

Тогда гиперболические функции в уравнениях передачи перейдут в тригонометрические:

.

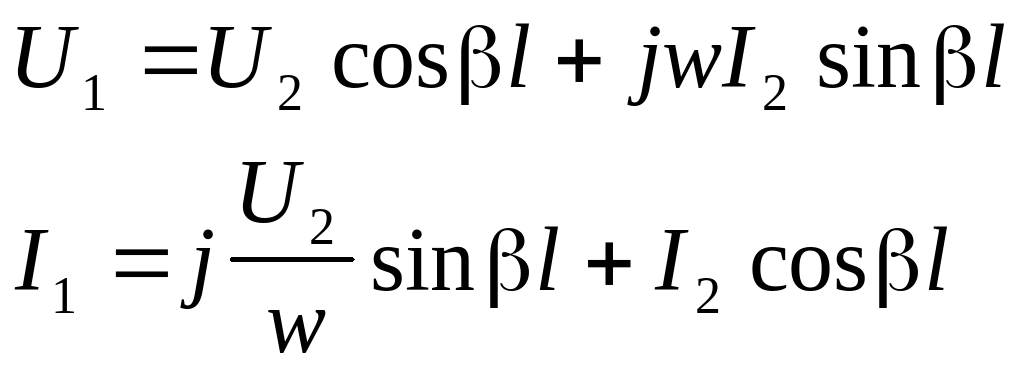Далее

С изменением l вектор (l) поворачивается, а длина его остается постоянной. Поворот происходит по часовой стрелке при движении в сторону генератора и против часовой стрелки при движении к нагрузке.

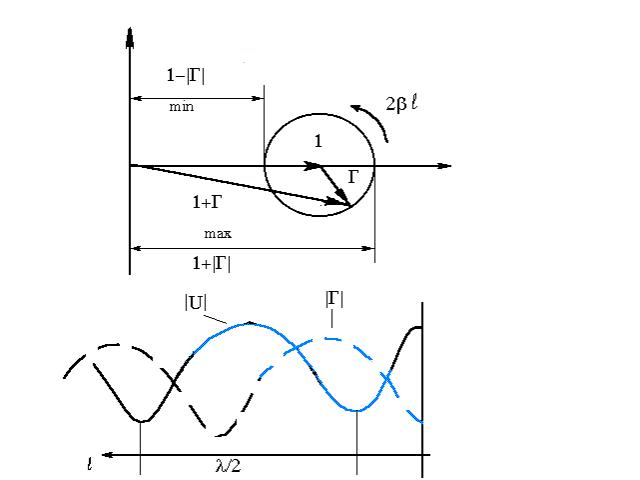
Полные напряжение и ток можно записать через (l)

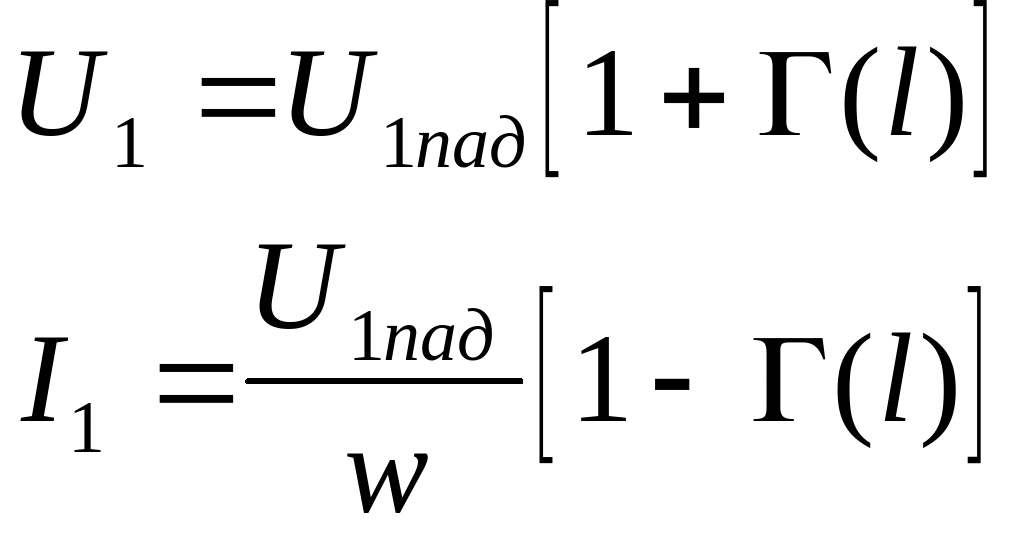
С изменением l модуль |U| изменяется пропорционально |1+|, так как |U_пад|=const. При движении вдоль линии конец вектора  описывает окружность радиуса ||, совершая полный оборот за /2. Поэтому имеет место чередование максимумов и минимумов амплитуд тока и напряжения. В точках, где |U| максимально, ток |I| минимален, и наоборот. Такая картина обусловлена интерференцией падающей и отраженной волн.

Отношение максимальной амплитуды напряжения (или тока) в линии к минимальной называется коэффициентом стоячей волны.

.

Обратная величина

называется коэффициентом бегущей волны.

Поскольку 0||1, то возможные значения этих величин лежат в пределах 1KСВ<, 0KБВ1. В РБВ KСВ =KБВ =1.

Величины ||, arg, KСВ, KБВ играют важную роль при измерениях в линиях и цепях СВЧ. Дело в том, что вольтметры, амперметры и т.п. приборы не годятся, т.к. их размеры вместе с соединительными проводами сравнимы с , т.е. получается цепь с распределенными параметрами, зачастую более сложная, чем измеряемая цепь. Однако можно измерить относительное распределение амплитуды |U|, перемещая вдоль линии небольшой зонд с подключенным к нему детектором (выпрямителем) на полупроводниковом диоде. Отсюда можно найти , , z_вх, z_н и ряд других величин. Подробнее эти вопросы изучаются на практических занятиях.

Абсолютные величины напряжения и тока на СВЧ измерить невозможно, но можно измерить мощность – по тепловому действию на эквивалент нагрузки, а через нее рассчитать U и I.