Длинные линии

В разделе 1 (часть 1) отмечалось, что основные постулаты и правила теории цепей (законы Кирхгофа) справедливы лишь в квазистационарном приближении. Предположение о том, что сила тока одинакова во всех сечениях провода, справедливо только для медленных колебаний, когда можно не учитывать конечную скорость с распространения электромагнитного поля по цепи, т.е. l/c<<T , где l –длина цепи, T – период колебаний. Поскольку cT=c/f=, данное условие принимает вид:

l<< (*)

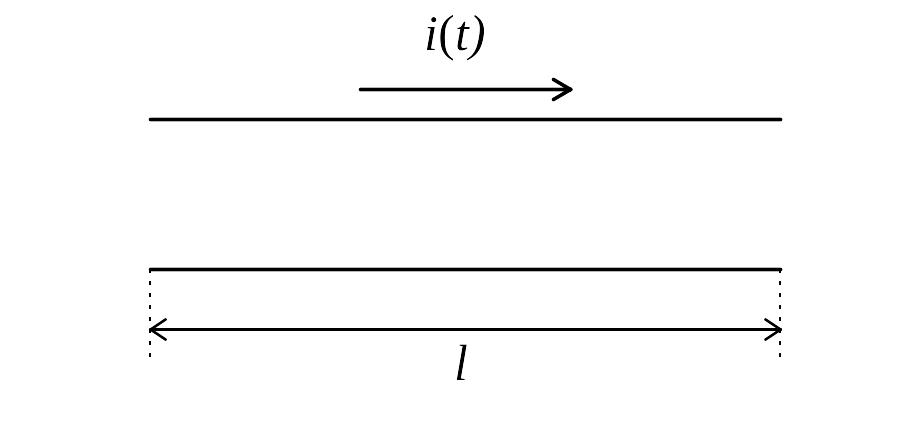
Если это условие не выполняется, ток в разных сечениях провода не будет одинаков (вследствие токов смещения).

Переменное электрическое поле не обладает потенциалом. Поэтому понятие напряжения можно использовать опять-таки только при относительно малых размерах цепи и его элементов, когда электрическое поле сосредоточено внутри конденсаторов, а магнитное поле в катушках. В остальной же части цепи можно пренебречь токами смещения и ЭДС магнитной индукции. Такие цепи называются цепями с сосредоточенными параметрами (качестве последних выступают R, L, C, M).

Если же размеры устройства сравнимы с , то в общем случае нужно оперировать непосредственно с напряженностями электрического и магнитного полей.

Существует, однако, класс устройств, которые хотя и не подчиняются условию (*), тем не менее понятия напряжения и тока для них можно сохранить. К ним относятся длинные линии.

Определение. Длинной линией называется система из двух (иногда более) проводников, длина которых сравнима или более, чем длина волны колебаний в них, а поперечные размеры системы малы по сравнению с длиной волны.

Длинные линии применяются для направленной передачи ВЧ и СВЧ колебаний (без потерь на излучение), а также используются в качестве резонансных систем на СВЧ.

Например, кабель, соединяющий антенну и ТВ приемник, длиной l=10 м следует рассматривать как длинную линию, так как для самой низкой частоты f=50 МГц (1-й канал) = 6 м. Однако тот же кабель для телефонного сигнала (f_max=10 кГц, =30 км) можно рассматривать как обычную пару проводов с сосредоточенными параметрами (R,C).

Наиболее часто применяются следующие конструкции линий:

Все поперечные размеры этих конструкций много меньше . Если профиль поперечного сечения не изменяется, линия называется однородной.

Условное обозначение длинной линии на расчетных схемах:

x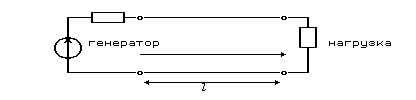

1. Дифференциальные уравнения длинной линии.

Если диэлектрическая среда однородна и потери энергии в ней отсутствуют, а проводимость проводников бесконечна, то в однородной вдоль x линии существует такое строгое решение задачи электродинамики, которое обладает следующими свойствами: 1)Векторы E и B в каждом сечении лежат в плоскости, перпендикулярной продольной оси x (отсутствуют E_x, B_x). При этом токи в проводах направлены вдоль x и сумма токов всех проводов равна 0. 2)Структура поля в поперечном сечении (т.е. зависимость поля от поперечных координат) такая же, как в соответствующем статическом случае.

Отметим, что возможны и совершенно другие решения уравнений поля, но мы сейчас будем интересоваться только этим.

Из сказанного следует, что если рассмотреть интеграл вдоль линии, соединяющий оба провода:

, (*)

то его величина не зависит от формы пути, если только весь путь лежит в одной поперечной плоскости. Это позволяет рассматривать данный интеграл как напряжение между проводами в сечении x.

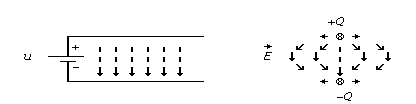
В электростатическом случае распределение поля в однородной линии постоянно вдоль x. Очевидно, заряд Q пропорционален напряжению и длине проводов: Q=Clu, где коэффициент C [Ф/м] есть емкость, приходящаяся на единицу длины. Он называется погонной емкостью длинной линии.

Аналогично, в магнитостатическом случае поле B пропорционально току i.

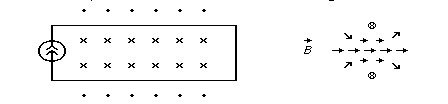
Следовательно, магнитный поток между проводами пропорционален току и длине: Ф=Lli. Коэффициент пропорциональности L [Г/м] называется погонной индуктивностью линии.

Теперь рассмотрим режим переменного тока. В этом случае ток и напряжение сохраняют смысл, но мы их должны считать функциями времени и координаты x: u(x,t), i(x,t).

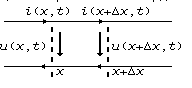
Выделим малый участок линии длиной x<<. Изменение напряжения на этом участке вызывается явлением электромагнитной индукции:

.

Изменение тока вдоль провода обусловлено наличием токов смещения:

.

Разделив на x и перейдя к пределу при x0, получим:

Это  уравнения длинной линии без потерь. Им отвечает представление участка цепи простой эквивалентной схемой (а). Чтобы учесть потери, в схему вводят элементы rx и gx (б), где r [Ом/м] погонное сопротивление проводников, g [См/м]  погонная проводимость утечки через диэлектрик.

Вообще говоря, при наличии потерь появляются продольные составляющие векторов E и B, и электрическое поле в поперечном сечении уже не будет потенциальным. Однако если потери малы, то характер поля незначительно отличается от рассмотренного выше, и понятие напряжения можно сохранить. "Уточненные" уравнения длинной линии имеют вид

(5.1)

Их иногда называют телеграфными уравнениями.

Проделанный нами вывод уравнений не является строгим. Однако более точная теория и эксперимент подтверждают справедливость этих уравнений для квазигармонических колебаний. Их можно применять и к неоднородным линиям, в этом случае погонные параметры (L, C, r, g) будут функциями x.

Поскольку процессы в линии удается описать посредством напряжений и токов, эти устройства относят к цепям, а именно к классу цепей с распределенными параметрами. Такие цепи описываются уравнениями в частных производных (в этом их существенное отличие от цепей с сосредоточенными параметрами).