1.2.3 Випадкові похибки вимірювання

Випадковою називають похибку, яка змінюється непе­редбачувано, нерегулярно, хаотично, випадковим чином під час повторних вимірювань однієї і тієї самої величини в однакових умовах.

Випадкові похибки виникають через велику кількість причин, які діють незалежно одна від одної. Це призво­дить до того, що результати окремих спостережень відріз­няються один від одного, причому ці зміни відбуваються без будь-якої закономірності.

Випадкові величини, в тому числі і випадкові похибки, характеризуються ймовірністю. Ймовірність випадкової величини і випадкової похибки зокрема показує, як часто трапляється конкретне значення ∆_і цієї величини і визначається відношенням кількості випадків n, коли випадко­ва похибка приймає дане конкретне значення ∆_і, до загальної кількості N випадків:

Р(∆)=ni/N.

Найбільш повною характеристикою випадкової похибки є функція розподілу ймовірностей і густина ймовірностей. Функція розподілу ймовірностей або закон розпо­ділу ймовірностей показує, яка ймовірність того, що випадкова похибка не перевищує дане значення, тобто який відсоток від загальної кількості похибок станов­лять похибки, які не перевищують дане значення.

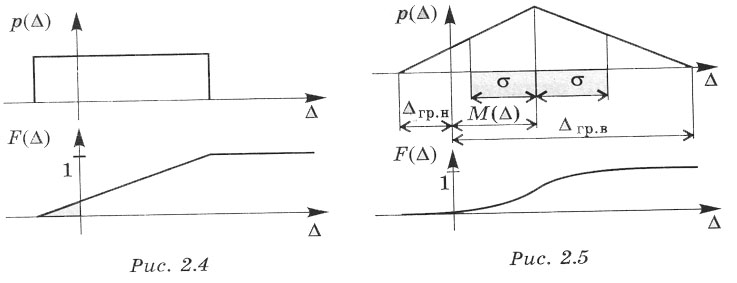
Зако­ни розподілу ймовірностей можуть бути обмеженими (рис. 2.4, 2.5), якщо випадкова похибка не виходить за певний діапазон значень, і необмеженими (рис. 2.6, 2.7), якщо випадкова похибка може мати будь-яке зна­чення на числовій осі. Слід зазначити, що необмежений закон розподілу ймовірностей - це лише зручна мате­матична модель для аналізу випадкових похибок на практиці.

Густина ймовірностей показує, як часто потрапляє ви­падкова величина, зокрема випадкова похибка ∆, в зада­ний інтервал

[∆₁, ∆₂] значень, і визначається відносною кількості випадків n_і/N, коли випадкова похибка знахо­диться в інтервалі [∆₁, ∆₂], до розміру цього інтервалу ∆₁₂=∆₂-∆₁

(2.9)

Густина ймовірностей визначається тим точніше, чим менший інтервал значень ∆₁₂ задається. Якщо спрямувати інтервал ∆₁₂ до нуля, то густина ймовірностей наближати­меться до теоретичного значення.

Розмірність густини ймовірностей обернена розмірно­сті випадкової похибки. 3 математичної точки зору, густина ймовірностей є похідною від функції розподілу ймовірностей:

(2.10)

За функцією розподілу ймовірностей та густиною ймовірностей, які несуть найбільш повну інформацію про випадкову величину, можна визначити деякі числові ха­рактеристики випадкової похибки: довірчий інтервал, довірчу ймовірність, математичне сподівання, середнє квадратичне відхилення.

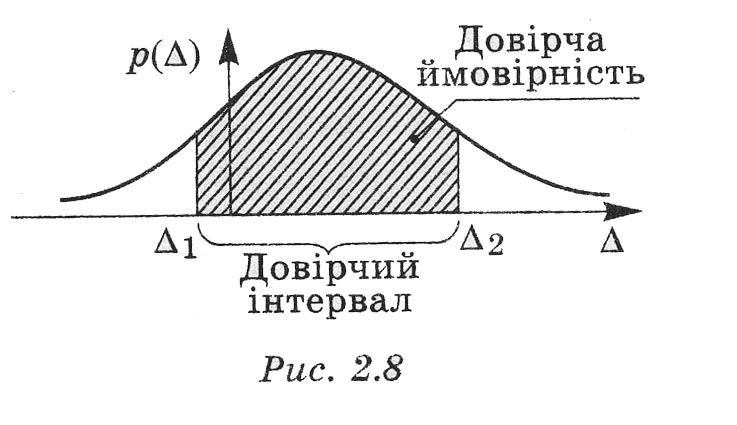
Довірчим інтервалом називається діапазон значень випадкової похибки, у якому знаходитимуться із зада­ною ймовірністю значення випадкової похибки. Ця ймо­вірність називається довірчою ймовірністю. Вона визначається за графіком густини ймовірностей як площа фігури, обмеженої графіком функцій, віссю абсцис і дво­ма вертикалями, проведеними через граничні значення довірчого інтервалу (рис. 2.8). У метрології часто ставиться задача: за заданим значенням довірчої ймовір­ності знайти довірчий інтервал. Іноді може бути обернена задача: за заданим довірчим інтервалом знайти довір­чу ймовірність.

Для законів розподілу ймовірностей визначаються

верхнє і нижнє граничні значення похибки, в діапазоні

між якими розподілені значення випадкової похибки.

Математичним сподіванням випадкової похибки М(∆) називається абсциса центра мас фігури, обмеженої графіком густини ймовірностей і віссю абсцис. Якщо випадкова похибка набуває значень ∆₁, ∆₂, ... ∆_n, то оцінка математичного сподівання похибки визначається середнім значенням:

(2.11)

Якщо виконати велику кількість вимірювань n, то середнє значення похибки наближається до математичного сподівання похибки, причому відхилення середнього зна­чення похибки від математичного сподівання тим менше, чим більшу кількість вимірювань виконано.

У метрології похибка вимірювання ∆ трактується в за­гальному випадку як випадкова похибка, яка має дві складові: систематичну складову ∆_S і випадкову складову ∆, математичне сподівання якої дорівнює нулю, тобто

(2.12)

Систематична складова ∆S похибки вимірювання ∆ дорівнює математичному сподіванню похибки вимірювання, тобто ∆S= М(∆).

Середнє квадратичне відхилення випадкової похибки дорівнює середній ширині густини ймовірностей.

Оцінку середнього квадратичного відхилення випадко­вої похибки можна обчислити за значеннями випадкових похибок ∆₁, ∆₂….∆_n згідно з формулою

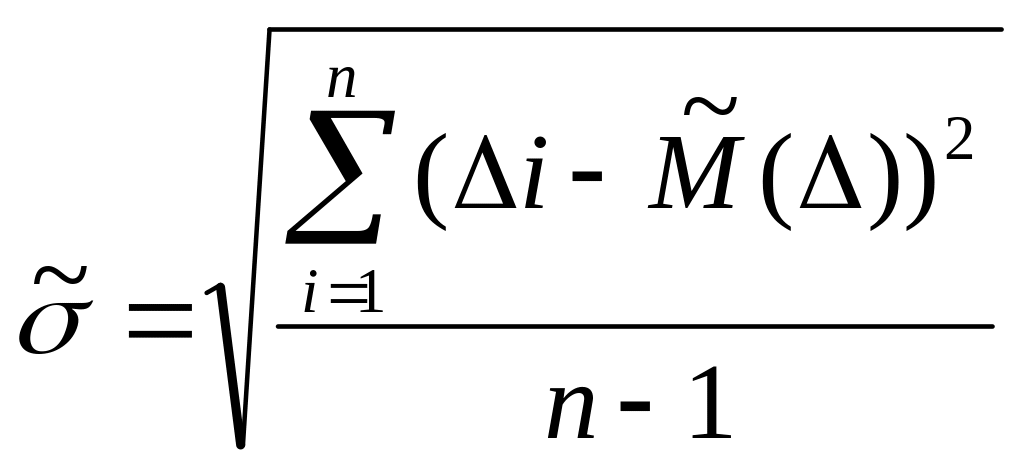(2.13)

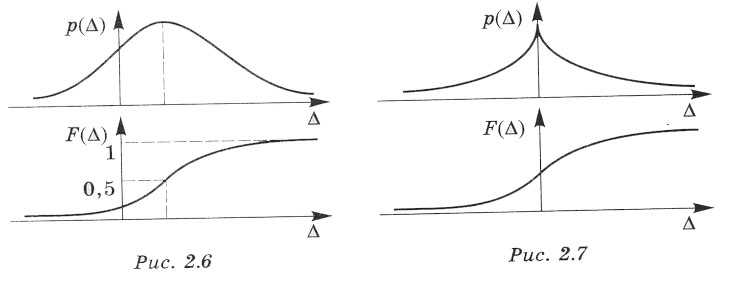
Якщо випадкова похибка вимірювання ∆ спричинена великою кількістю чинників, то вона має норРисьний закон розподілу ймовірностей.

Функція розподілу ймовірностей для норРисьного зако­ну виражається через так звану функцію Лапласа, значен­ня якої наведені в таблиці 2.1.

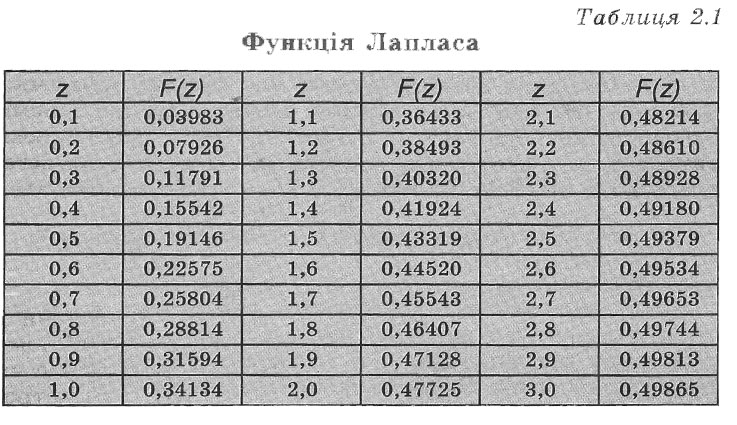
Графіки функції розподілу ймовірностей для норРись­ного закону наведені на рисунку 2.6. Параметр М(∆) характеризує зміщення на осі абсцис, а σ - середню ши­рину розподілу (див.рис. 2.5).

Похибка дискретизації та деякі інші похибки роз­поділені за рівномірним законом, тобто ймовірність того, що похибка вимірювання набуде конкретного значення у деякому діапазоні, однакова. Інакше кажучи, випадкова похибка вимірювання, розподілена за рівномірним зако­ном, трапляється однаково часто у всьому діапазоні значень (див, наприклад, графіки функцій розподілу ймовірностей та густини ймовірностей, наведені на

(рис. 2.4).

Якщо випадкова похибка має дві складові, розподілені за рівномірним законом з однаковим граничним значен­ням, то сумарна похибка розподілена за трикутним за­коном, або законом Сімпсона. Графіки густини ймовірно­стей і функції розподілу випадкової похибки, розподіленої за трикутним законом, наведені на рисунку 2.5.

Випадкова похибка, розподілена за законом Лапласа, має густину ймовірностей, подану на рисунку 2.7.

Зміст