§ V1.4. Давление насыщенного пара компоненте над раствором. Уравнения Рауля и Генри. Растворимость газов

Установим зависимость давления насыщенного пара растворителя и раст­воренного вещества от состава раствора и свойств чистых компонентов для идеальных, предельно разбавленных и неидеальных растворов. Для этого воспользуемся общей зависимостью давления насыщенного пара ком­понента раствора от химического потенциала и выразим в ней химический потенциал через состав для разных типов растворов.

Идеальные растворы. Подставляя в уравнения (VI. 18) выражения для хи­мического потенциала компонента идеального раствора из (VI.43) или (VI.45), получаем

(VI.51)

Интегрируя (VI.51) в пределах от р* до р , и от х = 1 до находим

(VI.52)

отсюда (VI.53)

(VI.54)

где р* — давление пара над жидким растворителем; р — давление пара над (чистым) жидким растворенным веществом. Выражения (VI.53) и (VI.54) называются законом Рауля или уравнениями Рауля. Равновесное парциальное давление пара компонента в идеальном растворе пропорционально молярной доле этого компонента в растворе. Зависимость парциального давления пара компонента от состава имеет вид прямой (рис. VI.2,a). Для твердого растворенного вещества p в уравнении (VI.54) представляет собой давление насыщенного пара над переохлажден­ной жидкостью при той же температуре (точка А', рис. VI.2,6). Уравнение Рауля позволяет установить зависимость давления пара над чистым твердым растворенным веществом от его растворимости в идеаль­ном растворе. В насыщенном идеальном растворе парциальное давление пара растворенного вещества над раствором р_2нас равно давлению насыщен­ною пара над твердым веществом р (т). При этом из уравнения Рауля получаем (рис. VL2,a)

(VI.55)

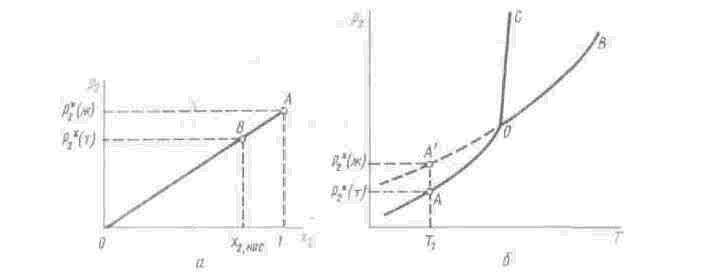
Рис. V1.2. Зависимость парциального давления пара растворенною вещества от ею молярной доли (а) и температуры (б) для идеальною pacтвopa

где Х_2нас — растворимость вещества в идеальном растворе, молярные доли. Из рис. V1.2, а видно, что справедливым будет соотношение

откуда и получается уравнение (VI.55).

Предельно разбавленные растворы. В предельно разбавленном растворе уравнение Рауля применимо к растворителю. По этому уравнению можно определить молекулярную массу М₂ нелетучего растворенного вещества, если известно давление пара растворителя над разбавленным раствором. Пре­образуя уравнение (VI.53) следующим образом:

Имеем

(VI.56)

где p /p* — относительное понижение давления пара растворителя над раст­вором; оно равно молярной доле растворенного вещества. Учитывая, что

получаем из уравнения (VI.56) выражение для определения молекулярной массы растворенного вещества

где М — молекулярная масса растворителя; — масса растворителя; — масса растворенного вещества. К растворенному веществу в предельно разбавленном растворе формула Рауля не применима (см. § VI.3). Однако из уравнения Гиббса — Дюгема для химического потенциала (VI.14) можно вывести зависимость парциаль­ного давления пара растворенного вещества над предельно разбавленным раствором от состава раствора. Подставляя в уравнение (VI. 14) значения d и d из (VI.43) и (VI.19), получаем

Учитывая, что и , преобразуем правую часть уравнения (VI.58)

и получаем (VI.59)

После интегрирования (VI.59) получим

где In К — постоянная интегрирования, откуда р₂ = К . (VI.60)

Выражение (VI.60) называется законом или уравнением Генри. Из закона Генри следует, что парциальное давление пара растворенного вещества над предельно разбавленным раствором пропорционально молярной доле раство­ренного вещества в этом растворе. Постоянная Генри К определяется экстраполяцией опытных данных:

Растворимость газов. Уравнение Генри (VI.60) имеет большое практическое значение для изучения растворимости газов в растворах. Если растворен­ное вещество — газ, то х₂ в уравнении (VI.60) представляет собой раство­римость газа в растворе при давлении р₂. Из уравнения Генри следует, что в предельно разбавленных растворах растворимость газов пропорциональна их парциальному давлению над раствором. Из (VI.60) получаем

где х — молярная доля растворенного газа; 1/К₂ — константа, зависящая от температуры; р₂ —давление газа над раствором. На практике количество растворенною газа принято выражать не в мо­лярных долях, а в объемных единицах. Если объем газа измеряется при температуре опыта, то уравнение Генри имеет вид

(V1.61)

где К_раст — коэффициент растворимости. Таким образом, коэффициент раст­воримости — это объем газа (измеренный при температуре опыта), который растворяется при данной температуре в единице объема растворителя при парциальном давлении газа, равном единице (1 МПа). Если объем газа измеряется при температуре 273 К, то видоизмененное уравнение Генри имеет вид

(VI .62)

где К_погл — коэффициент поглощения газа. Он представляет собой объем газа (измеренный при 273 К), который растворяется в единице объема раство­рителя при парциальном давлении газа р₂, равном единице (1 МПа). Между этими коэффициентами имеется простое соотношение, которое получается, если разделить уравнение (VI.61) на (VI.62), полагая р₂ одинаковыми (p₂ = const): К_раст/К_погл = V_т/V_o. Принимая, что газ подчиняется законам идеаль­ного газа и, в частности, закону Гей-Люссака (V_т/V_о = Т/273), получим искомое соотношение

Растворимость газов в водных растворах электролитов определяется по эмпирическому уравнению И. М. Сеченова

=Кс, где S⁰ — растворимость газа в воде; S — растворимость газа в растворе электролита; К—коэффициент; с—концентрация электролита в растворе. Растворимость газа в воде всегда больше растворимости его в растворе электролита.

Неидеальные растворы. Для неидеальных растворов в уравнение (VI. 19) нужно подставить выражение для химического потенциала (VI.49) или (VI.50), тогда

ln p =d ln a (VI.63) После интегрирования получим

где In К, — постоянная интегрирования. Для растворителя и растворенного вещества получим соответственно

(VI.64) Если оба компонента — взаимно растворимые жидкости, то за стандарт­ное состояние выбирают чистое вещество. При этом уравнения для давления пара над раствором имеют вид