4. Ввод формул для вычислений значений целевой функции и левой части неравенств

Чтобы вычислить значение целевой функции и левой части неравенств, не обходимо найти суммы произведений коэффициентов на соответствующие переменные в ячейках D4, D7, D8, D9,:

• в ячейке D4 следует ввести соответствующую формулу (рис. 18) или воспользоваться встроенной функцией =СУММПРОИЗВ() (рис. 19);

• набранную формулу можно скопировать, для этого необходимо ссылки на ячейки со значениями переменных B3 и B4 сделать абсолютными ($B$3 и $B$4) с помощью клавиши F4 или набрать знак $ на клавиатуре. Абсолютная ссылка на ячейку при копировании не изменяется, для ее обозначения используется знак $;

• чтобы скопировать формулу из ячейки D4 в ячейки D7, D8 и D9 (рис. 18, 19), применяется способ копирования с помощью буфера обмена (команды Копировать, Вставить или комбинации клавиш CTRL+C, CTRL+V).

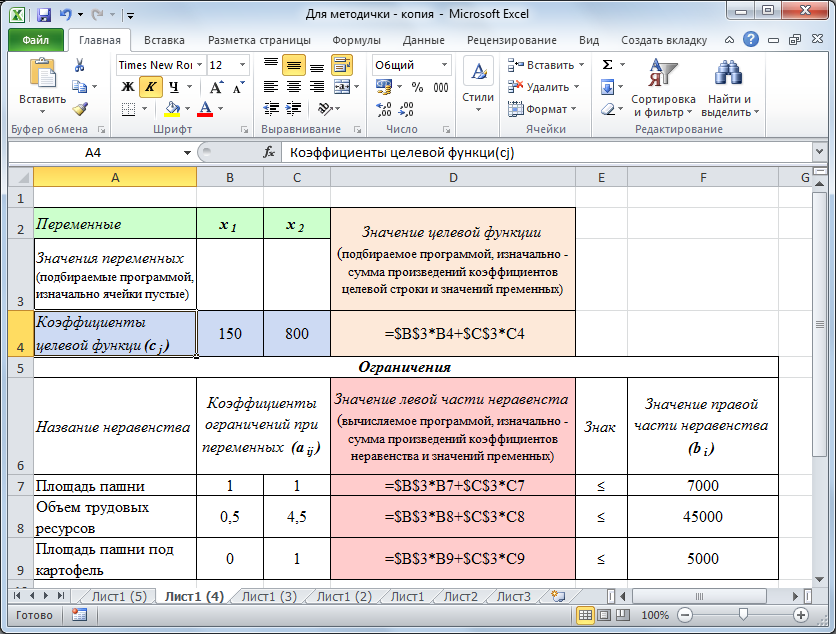
Рис. 18 – Формулы для вычислений значений целевой функции и левой части ограничений с помощью формул

Рис. 19 – Формулы для вычислений значений целевой функции и левой части ограничений с помощью функции =СУММПРОИЗВ()

5. Настройка программы Microsoft Excel 2010

Команда Поиск решения находится во вкладке Данные, если выполнена настройка программы (Файл | Параметры | Надстройки | Поиск решения| Перейти) (рис. 20).

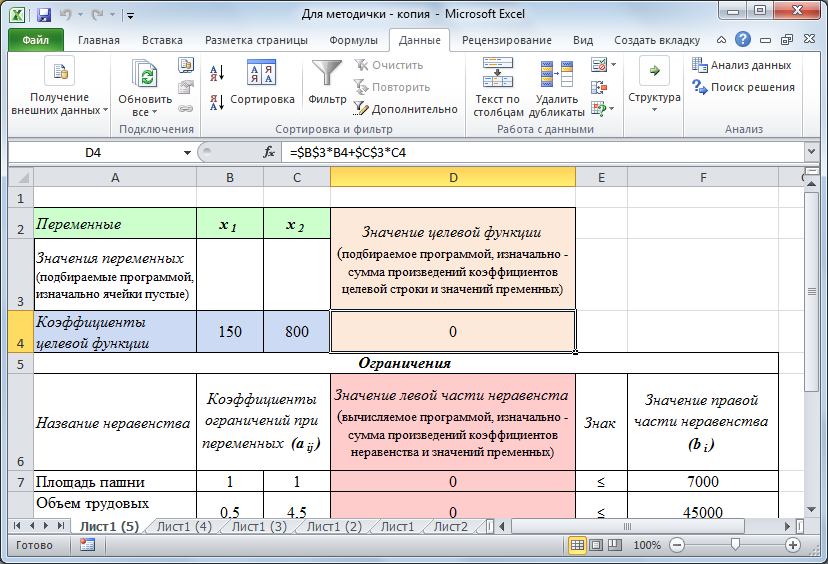
Рис. 20 – Команда Поиск решения на вкладке Данные и окно Параметры поиска решения

6. Установка значений в окне Параметры поиска решений

Откройте окно Поиска решений и введите (рис. 21):

• адрес ячейки со значением целевой функции – $D$4 (щелчком левой кнопки мыши по ячейке D4, знаки «$» появятся автоматически);

• установите режим Максимум;

• в поле Изменяя ячейки переменных укажите диапазон $B$3: $C$3, в которых программа подберет оптимальные значения переменных x₁ и х₂;

• добавьте ограничения с помощью кнопки Добавить (рис. 21). Для этого используется щелчок левой кнопки мыши по необходимым ячейкам, а знак неравенства или равенства выбирается из списка в окне Добавление ограничения (рис. 22);

• установите режим Сделать переменные без ограничений неотрицательными, соответственно условию неотрицательности переменных x₁ и х₂ (рис. 21);

• укажите метод решения Поиск решения линейных задач симплексным методом (рис. 21);

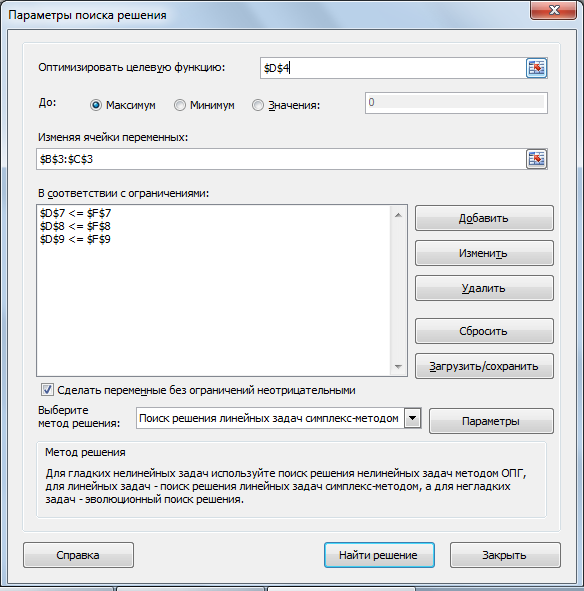
Рис. 21 – Окно Параметры поиска решения

Рис. 22 – Окно Добавление ограничения

• нажмите кнопку Найти решение (рис. 21);

• в окне Результаты поиска решения выберите режим Сохранить найденное решение и нажмите ОК (рис. 23).

Рис. 23 – Окно Результаты поиска решения

7. Анализ полученного решения

Программа вычислила решение (рис. 24).

Если по каким-то причинам (изменение исходных данных, ошибка при вводе ограничений или установке режимов) необходимо решить задачу заново, то следует исправить ошибку, удалить ранее найденные значения переменных x₁ и х₂ (т.е. очистить ячейки B3 и C3), вызвать команду Поиск решений, проверить и изменить введенные в окне Параметры поиска решений установки и нажать на кнопку Найти решение (рис. 21).

Если решение выполнено без ошибок, то следует записать ответ. Количество недоиспользованных ресурсов необходимо вычислить самостоятельно. Например, в данной задаче (рис. 24) объем трудовых ресурсов составил 23500 чел.-дней, тогда количество недоиспользованных трудовых ресурсов составит 45000 – 23500 = 21500 (чел.-дней).

Рис. 24 – Оптимальное решение задачи симплексным методом

Ответ: Оптимальное сочетание посевов (2000 га – площадь ячменя, 5000 га – площадь картофеля) позволит получить максимум прибыли – 4300000 ден. ед., при этом будет недоиспользовано 21500 чел.-дней трудовых ресурсов.

Вопросы

1. Каков план решения задачи симплексным методом в Microsoft Excel?

2. Что такое Поиск решений? Как настроить программу Microsoft Excel 2010 для работы с Поиском решений?

3. Какие установки выполняются в окне Параметры поиска решений?

4. Какие действия необходимо выполнить, чтобы решить задачу с другими исходными данными или ограничениями?

Рекомендуемые источники к главе 5

4, 7, 8, 10, 15, 22

6. Распределительный метод решения задач линейного программирования. Транспортная задача

6.1. Задачи линейного программирования, решаемые распределительным методом

Распределительный метод решения задач (метод транспортной задачи) относится к группе оптимизационных методов решения задач линейного программирования. Это частный случай симплексного метода.

Название транспортной задачи обусловлено тем, что этот метод разработан применительно к организации перевозок груза. Метод отображен в работах А.Н. Толстого, опубликованных в 1930 году.

В настоящее время методы решения транспортных задач применяются в следующих случаях:

• распределение культур по предшественникам, чтобы получить максимум валовой продукции;

• распределение работ по маркам тракторов;

• оптимизация электрических сетей;

• размещение ремонтного фонда по мастерским и т.д.

Наибольшее распространение распределительный метод получил при оптимизации грузоперевозок. Возможно большое количество вариантов плана перевозок различных грузов, поэтому возникает проблема рационального использования транспортных средств. Эту проблему решают с помощью математических методов и программных средств, что позволяет определить наиболее эффективные способы организации транспортных средств и рассчитать оптимальные схемы грузоперевозок. В настоящее время разработано около двадцати постановок транспортных задач и существует более десяти методов их решения (метод потенциалов или модифицированный распределительный метод, распределительный метод, метод дифференциальных рент, дельта-метод и т.д.).