6. Построение второй симплексной таблицы

Для того, чтобы составить новый план решения задачи, необходимо построить вторую симплексную таблицу, которая заполняется с помощью разрешающего элемента.

Шаг 1. В первой симплексной таблице добавим вспомогательный столбец и определим разрешающий столбец, разрешающую строку и разрешающий элемент (таблица 6).

Таблица 6

Первая симплексная таблица с разрешающим элементом

Базис	Свободные члены, bi	Свободные переменные			Симплексные отношения (вспомогательный столбец)
		-х1	-х2
S1	7000	1	1	7000
S2	45000	0,5	4,5	10000
S3	5000	0	1	5000
Z	0	-150	-800	–

Разрешающий столбец при решении задач на максимум с естественным базисом определяется по наименьшему отрицательному коэффициенту целевой строки Z; при решении задач на минимум – по набольшему положительному коэффициенту целевой строки Z.

В рассматриваемом примере наименьший отрицательный коэффициент целевой функции равен -800, следовательно, он указывает на разрешающий столбец симплексной таблицы (таблица 6).

При решении задач на максимум и минимум разрешающая строка находится по наименьшему положительному симплексному отношению, т.е. частному от деления коэффициентов столбца свободных членов на соответствующие коэффициенты полученного разрешающего столбца.

Чтобы определить разрешающую строку находим симплексные отношения в каждой строке (делим свободные члены на соответствующие им значения в разрешающем столбце) и записываем их во вспомогательный столбец (таблица 6). Например, в первой строке свободный член равен 7000, коэффициент в разрешающем столбце равен 1. Следовательно, симплексное отношение для первой строки находим так: .

Запишем симплексные отношения для второй и третьей строк симплексной таблицы: 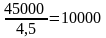и .

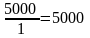На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент (генеральный элемент), который выделяют в таблице и обозначают А.

В примере разрешающий элемент равен 1, обозначен буквой А (таблица 6).

Шаг 2. Заполняем вторую симплексную таблицу (таблица 7):

• свободная и базисные переменные, соответствующие разрешающему столбцу и разрешающей строке меняются местами. В данном случае переменная х₂ становится базисной, S_3­ – свободной;

• остальные коэффициенты второй симплексной таблицы находятся по правилам.

Таблица 7

Вторая симплексная таблица

Базис	Свободные члены, bi	Свободные переменные
		-х1	-S3
S1			-1
S2			-4,5
х2	5000	0	1
Z			800