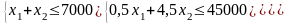- •Методы оптимальных решений
- •Содержание
- •Введение
- •1. Моделирование – метод научного познания
- •1.1 Основные понятия моделирования
- •Вопросы *
- •1.2 Системный подход и моделирование социально-экономических систем
- •Вопросы
- •5. Численное решение
- •6. Анализ численных результатов и их применение
- •Приемы экономико-математического моделирования
- •Классификация моделей по типу информации:
- •Классификация моделей по учету фактора времени:
- •Классификация моделей по учету фактора неопределенности:
- •Классификация моделей по типу подхода к изучаемым социально-экономическим системам:
- •Вопросы
- •2.2 Принцип оптимальности в планировании и управлении
- •Вопросы
- •Математическая формулировка общей задачи линейного программирования
- •Структурная форма записи задачи линейного программирования
- •Вопросы
- •3.2 Формы записи задачи линейного программирования
- •Нормы затрат и выхода продукции
- •Решение
- •Общая форма записи задачи линейного программирования
- •Каноническая форма записи задачи линейного программирования
- •Стандартная форма записи задачи линейного программирования
- •4.2. Алгоритм графического метода
- •Нормы затрат и выхода продукции
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Построение граничных прямых, соответствующих системе ограничений
- •3. Определение области допустимых решений
- •4. Построение вектора градиента и линии уровня
- •5. Нахождение точки экстремума
- •6. Определение значения целевой функции
- •4.3. Варианты графического решения задач линейного программирования
- •Вопросы
- •Рекомендуемые источники к главе 4
- •5. Симплексный метод решения задач линейного программирования
- •5.1. Сущность симплексного метода
- •Вопросы
- •5.2. Алгоритм решения задач симплексным методом с естественным базисом
- •Показатели эффективности возделывания 1 га культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса
- •4. Построение первой симплексной таблицы
- •Первая симплексная таблица (сокращенная)
- •Первая симплексная таблица (полная)
- •5. Проверка оптимальности решения
- •6. Построение второй симплексной таблицы
- •Первая симплексная таблица с разрешающим элементом
- •Вторая симплексная таблица
- •Правила нахождения коэффициентов второй симплексной таблицы
- •Вторая симплексная таблица
- •7. Построение третьей и последующих симплексных таблиц
- •Вторая симплексная таблица с разрешающим элементом
- •Третья симплексная таблица
- •Вопросы
- •5.3. Алгоритм решения задач симплексным методом с искусственным базисом
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса, введение искусственных переменных
- •4. Построение первой симплексной таблицы
- •Первая сокращенная симплексная таблица с м-строкой
- •5. Решение вспомогательной задачи симплексным методом с естественным базисом
- •Данные о содержании питательных веществ и стоимости культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Составление базиса, введение искусственных переменных
- •4. Построение первой симплексной таблицы
- •Первая симплексная таблица
- •5. Проверка оптимальности решения
- •6. Построение второй симплексной таблицы
- •Первая симплексная таблица с разрешающим элементом
- •Вторая симплексная таблица
- •7. Построение третьей и последующих симплексных таблиц
- •Третья симплексная таблица
- •Вопросы
- •5.4. Алгоритм решения задач симплексным методом в Microsoft Excel 2010
- •Показатели эффективности возделывания 1 га культур
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Составление формы для ввода данных в Microsoft Excel
- •3. Ввод исходных данных в форму Microsoft Excel
- •4. Ввод формул для вычислений значений целевой функции и левой части неравенств
- •5. Настройка программы Microsoft Excel 2010
- •6. Установка значений в окне Параметры поиска решений
- •7. Анализ полученного решения
- •6.2. Постановка и математическая формулировка транспортной задачи
- •Постановка задачи
- •Матрица транспортной задачи
- •6.3. Алгоритм решения транспортной задачи (метод северо-западного угла)
- •Стоимости перевозок одной тонны картофеля (ден. Ед.)
- •Решение
- •1. Проверка типа задачи (открытая или закрытая)
- •2. Составление экономико-математической модели задачи
- •Матрица транспортной задачи (ден. Ед.)
- •3. Составление опорного плана
- •Опорный план транспортной задачи (ден. Ед.)
- •4. Проверка решения на оптимальность
- •Опорный план транспортной задачи (ден. Ед.)
- •5. Построение контура
- •Правила построения контура
- •Опорный план транспортной задачи с контуром (ден. Ед.)
- •6. Построение нового опорного плана
- •7. Проверка нового плана на оптимальность
- •Вопросы
- •6.4. Алгоритм решения транспортной задачи в Microsoft Excel 2010
- •Себестоимость перевозки 1 т сена, руб.
- •Решение
- •1. Проверка типа задачи (открытая или закрытая)
- •2. Составление экономико-математической модели задачи
- •6. Анализ полученного решения
- •Вопросы
- •6.5. Задача о назначениях
- •Общий вид транспортной матрицы задачи о назначениях
- •Экономико-математическая модель задачи о назначениях
- •Структурная форма записи задачи о назначениях
- •Вопросы и задания для самопроверки и самоподготовки
- •6.6. Алгоритм решения задачи о назначениях с помощью Microsoft Excel 2010
- •Производительность работников
- •Решение
- •1. Составление экономико-математической модели задачи
- •7.2 Прямая и двойственная задача
- •Построение двойственной задачи
- •Исходные данные задачи
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Приведение модели к канонической форме записи задачи, определение основных и дополнительных переменных
- •3. Решение задачи симплексным методом
- •Последняя симплексная таблица (оптимальное решение)
- •4. Анализ двойственных оценок
- •Симплексная таблица с коэффициентами замещения и двойственными оценками
- •Вопросы
- •7.3 Основные свойства двойственных оценок
- •Вопросы
- •7.4 Алгоритм решения двойственной задачи в Microsoft Excel 2010
- •Решение
- •1. Составление экономико-математической модели задачи
- •2. Решение задачи симплексным методом
- •3. Анализ оптимального решения
- •4. Мера влияния ограничения на целевую функцию
- •5. Свойство оптимальности решения
- •Вопросы
- •Рекомендуемые источники к главе 7
- •Библиографический список
- •Приложение 1 Полезные ссылки
Рекомендуемые источники к главе 4
4, 7, 8, 15, 22
5. Симплексный метод решения задач линейного программирования
5.1. Сущность симплексного метода
Симплексный метод – это метод решения задач линейного программирования, основанный на принципе последовательного улучшения решения. Применяется только к задачам в канонической форме записи.
Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число шагов. Каждый из шагов (итераций) состоит в нахождении нового плана, которому соответствует более близкое к оптимальному значение целевой функции по сравнению с предыдущим планом. Процесс вычисления продолжается до получения оптимального плана.
Решение задач симплексным методом проводится по этапам:
Создается экономико-математическая модель в канонической форме.
Указывается способ вычисления начального (опорного) решения.
При помощи признака оптимальности проверяется, является ли это решение оптимальным.
По выбранному начальному решению строится другое, более близкое к оптимальному.
Процесс вычисления продолжается до получения оптимального плана.
В зависимости от типа ограничений в системе задачи линейного программирования могут решаться симплексным методом с естественным и искусственным базисом:
если все ограничения в системе типа «≤», то задача решается симплексным методом с естественным базисом;
если в системе ограничений встречается хотя бы одно ограничение типа «≥» или «=», то задача решается симплексным методом с искусственным базисом.
Симплексным методом с естественным базисом на минимум реальные экономические задачи не решаются, только математические.
Вопросы
В чем суть симплексного метода?
Назовите отличительные признаки в условиях задач, определяющие их возможность решения симплексным методом.
Каковы этапы решения задач линейного программирования симплекс-методом?
В каких случаях применяется симплексный метод решения задач с естественным базисом?
Когда возникает необходимость использования симплексного метода с искусственным базисом?
5.2. Алгоритм решения задач симплексным методом с естественным базисом
Алгоритм решения задачи рассмотрим на конкретном примере.
Задача 3. Найти оптимальное сочетание посевов ячменя и картофеля, если известно, что выделено пашни 7000 га, трудовых ресурсов – 45000 чел. – дней. Площадь под картофель не должна превышать 5000 га. Определить оптимальное сочетание посевов этих культур, обеспечивающее максимум товарной продукции в денежном выражении. Эффективность возделывания 1 га этих культур характеризуется показателями (таблица 3):
Таблица 3
Показатели эффективности возделывания 1 га культур
Показатели |
Ячмень |
Картофель |
Урожайность, ц/га |
15 |
100 |
Затраты труда, чел.-дней на га |
0,5 |
4,5 |
Цена 1 ц, ден. ед. |
10 |
8 |
Решение
1. Составление экономико-математической модели задачи
Обозначения: x1 – площадь ячменя, га; х2 – площадь картофеля, га.
Экономико-математическая модель задачи в общей форме: Найти значение неизвестных, которое бы обеспечивало максимальное значение целевой функции Zmax при соблюдении ограничений и условий неотрицательности переменных:
1) целевая функция: Zmax = 150х1 + 800х2 (ден. ед.);
2) система ограничений:
|
– ограничение на площадь пашни (га) – ограничение на объем трудовых ресурсов (чел.-дней); – ограничение на площадь пашни под картофель (га) |
3) условия неотрицательности: x1≥ 0, x2 ≥ 0.