3. Определение области допустимых решений

Находим область решений каждого неравенства, а затем общую область допустимых решений всей системы неравенств.

Площадь, занимаемая картофелем и кукурузой, не может быть отрицательной, поэтому решение будет располагаться в I четверти (в верхнем правом квадранте), т.е. область допустимых решений будет ограничена осями координат. Граничные прямые l₁, l₂, l₃ пресекаясь, составляют в I четверти выпуклый многоугольник B₃CDB₂. Каждая точка этого многоугольника удовлетворяет системе ограничений задачи, следовательно, множество точек этого многоугольника образуют область допустимых вариантов плана (рис. 13).

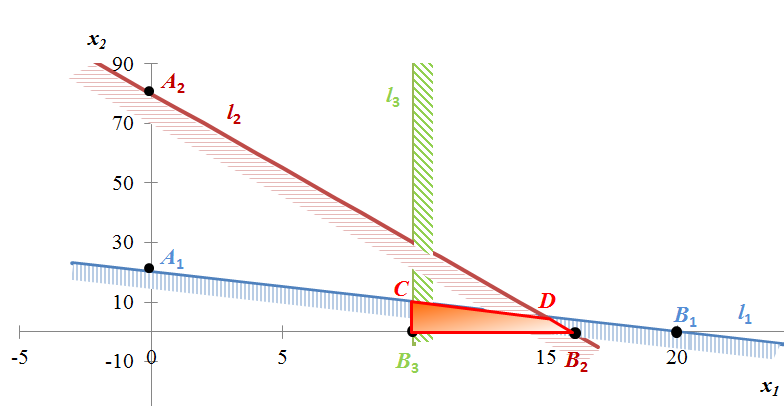
Рис. 13 – Область допустимых решений B₃CDB₂

4. Построение вектора градиента и линии уровня

Вектор-градиент строится по двум точкам, координатами которых являются коэффициенты при переменных целевой функции. В данном примере это точки О (0; 0) и N (80; 35). Линию уровня Z(x) = 0 проведем через точку О (0; 0), перпендикулярно вектору-градиенту (рис. 14).

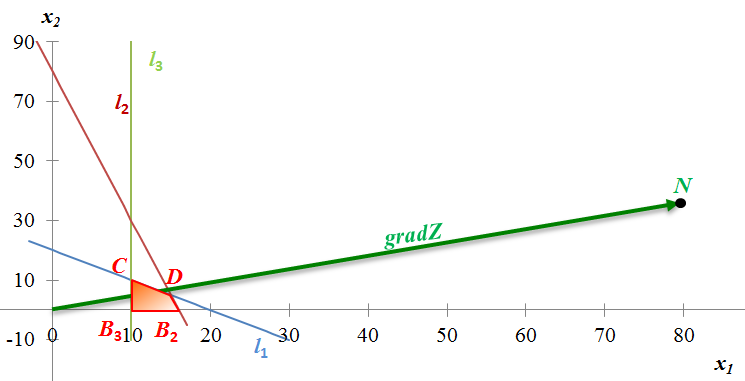
Рис. 14 – Вектор-градиент gradZ

5. Нахождение точки экстремума

Чтобы определить точку экстремума, передвинем линию уровня в направлении вектора-градиента gradZ(x) до крайней точки касания c многоугольником решений. Последней точкой касания является точка D (рис. 15).

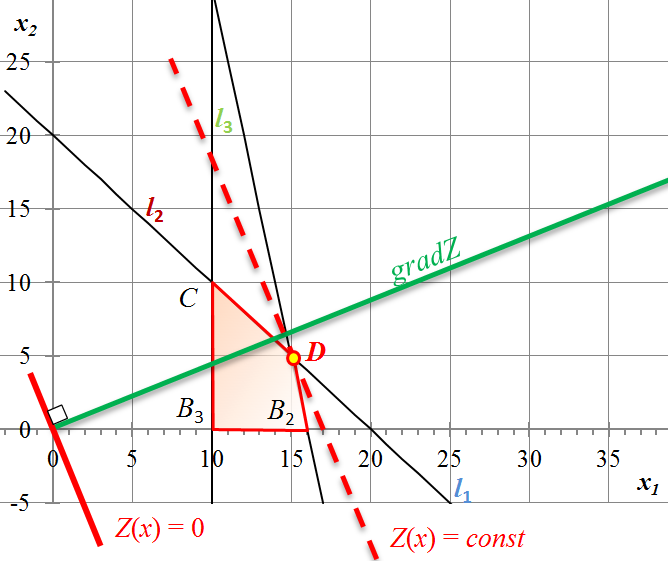
Рис. 15 – Линия уровня Z(x) = const, D – точка экстремума

Чтобы вычислить координаты точки экстремума D, необходимо определить, какие прямые пересекаются в этой точке (достаточно выбрать две прямые), и решить систему уравнений, соответствующую этим двум прямым.

В точке D пересекаются прямые l₁ и l₂, поэтому решив систему уравнений:

,

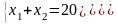найдем координаты этой точки D (15; 5).

Итак, x₁ = 15, x₂ = 5. Тогда площадь, занимаемая под картофель, составляет 15 га, площадь под кукурузу на зерно – 5 га.

6. Определение значения целевой функции

Найдем значение целевой функции в точке экстремума:

Z_max (D) = Z_max (15; 5) = 80 × 15 + 35 × 5 = 1200 + 175 = 1375 (ден. ед.).

Ответ: Оптимальным сочетанием площадей посевов является структура, в которой площадь под картофель составляет 15 га, площадь под кукурузу – 5 га. При этом будет получена максимальная прибыль 1375 ден. ед.

4.3. Варианты графического решения задач линейного программирования

При решении задач линейного программирования графическим методом встречаются различные варианты.

1. Решение достигается в одной из вершин симплексного многоугольника (рис. 11, 15).

2. Оптимальное решение существует и достигается на отрезке (рис. 4, 6). В этом случае, задача имеет множество оптимальных решений, которые называются альтернативными оптимальными решениями или альтернативным оптимумом.

3. Оптимальное решение существует и достигается в единственной возможной точке, соответствующей системе ограничений задачи (рис. 7).

4. Решение может быть в одной точке (рис. 5).

5. Отсутствие общей области допустимых решений (рис. 8), означает несовместимость системы ограничений, что требует корректировки условий задачи.

Вопросы

1. В чем заключается геометрическая интерпретация задачи линейного программирования?

3. Каковы основные этапы решения задач линейного программирования графическим методом?

4. Существуют ли ограничения на применение решения задач графическим методом? Перечислите их.

5. Что такое симплекс?

6. Что такое область допустимых решений?

7. Как определить область допустимых решений на графике?

8. Что такое граничная прямая и как ее построить?

9. Какое значение для решения задачи имеет расположение полуплоскости относительно граничной прямой?

10. Объясните геометрический смысл неравенства и уравнения.

11. Нарисуйте возможные варианты области допустимых решений.

12. Что такое вектор-градиент и линия уровня?

13. Каковы правила построения вектора-градиента и линии уровня?

14. Как найти точку экстремума?

15. Как определить на графике направление оптимизации?

16. Как вычислить экстремальное значение целевой функции?

17. Нарисуйте варианты графического решения задач линейного программирования.

18. При каких условиях оптимальное решение единственное, а при каких – их множество? Как изменяется при этом значение функции цели?

19. Как осуществить контроль правильности решения задачи?

20. В каком случае задача имеет бесчисленное число оптимальных решений при неизменном значении функции цели?