Часть 2

10. Поместите пробную катушку в центр витка и замкните ключ К.

11. Установите максимальную силу тока в витке, запишите значение силы тока в таблицу 4.3 и разомкните ключ К.

Таблица 4.3

Зависимость показания гальванометра от расстояния между витком и пробной катушкой

Номер замера	x	α
	см
1
2
…
…
8

12. Глядя на экран баллистического гальванометра, замкните ключ К, уловите момент, когда «зайчик» на экране достигнет максимального отклонения, и запишите это отклонение α в таблицу 4.3. Затем разомкните ключ К.

13. Передвиньте пробную катушку вдоль оси витка (по линейке) на 3 см и запишите отсчёт по линейке x (расстояние между плоскостью витка и пробной катушкой) в таблицу 4.3. Затем выполните пункт 4.12.

14. Повторите пункт 4.13 ещё 6 раз.

5. Обработка результатов измерений

1. На основании таблицы 4.2 постройте график зависимости максимального отклонения «зайчика» α от силы тока в витке I.

• Выделите для графика не менее половины страницы.

• Выберите подходящий масштаб, имея в виду, что по горизонтальной оси (оси абсцисс) надо откладывать значения силы тока в витке I, а по вертикальной оси (оси ординат) – значения α.

• Нанесите на график экспериментальные точки в виде не закрашенных кружочков диаметром примерно 2 мм.

• Нанесите на график планки погрешностей. Это значит, что надо от каждой экспериментальной точки отложить влево и вправо отрезок длиной (I), а затем отложить вверх и вниз отрезок длиной (α).

Проведите по линейке экспериментальную прямую – так, чтобы она пересекла планки погрешностей всех экспериментальных точек, причём прошла наиболее близко ко всем точкам и через начало координат. Образец показан на рисунке 5.1.

2. И змерьте угловой коэффициент E экспериментальной прямой линии.

Для этого выберите на экспериментальной прямой линии две произвольную точку A и определите её координаты 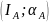. После этого E можно определить по формуле

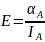. (5.1)

Например, на рисунке 4.1 выбрана точка A с координатами (100 мА; 36,2). При этом получается:

.

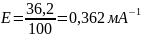Обратите внимание, как выбрана точка A: справа от всех экспериментальных точек.

Графики можно строить, используя современные компьютерные программы. Например, график на рисунке 5.1 построен с помощью EXCEL. Программа сама провела по точкам экспериментальную линию (линию тренда) и выдала её уравнение: y = 0,3603x. Из этого уравнения видно, что .

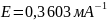3. Используя формулу (2.12) , определите значение коэффициента C.

4. Оцените погрешности измерений (E) и (C). Как это сделать, написано в пункте 6.

5. Заполните таблицу 5.1.

• Перенесите в неё данные из таблицы 4.3.

• Определите по формуле (2.8): 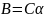значение магнитной индукции B в точках, в которых располагалась пробная катушка.

• Определите по формулам (1.10): значения вспомогательных величин y и z для каждого из замеров.

6. На основании таблицы 5.1 постройте график зависимости между вспомогательными величинами y и z.

• Выделите для графика не менее половины страницы.

• Выберите подходящий масштаб, имея в виду, что по горизонтальной оси (оси абсцисс) надо откладывать значения y, а по вертикальной оси (оси ординат) – значения z.

• Нанесите на график экспериментальные точки в виде не закрашенных кружочков диаметром примерно 2 мм.

Таблица 5.1

Магнитная индукция на оси витка

Номер замера	x	α	B
	см		мкТл	см2	мкТл-2/3
1
2
3
…
…
8

• Нанесите на график планки погрешностей. Это значит, что надо от каждой экспериментальной точки отложить влево и вправо отрезок длиной (y), а затем отложить вверх и вниз отрезок длиной (z). Как оценить погрешности (y) и (z), написано в пункте 6.

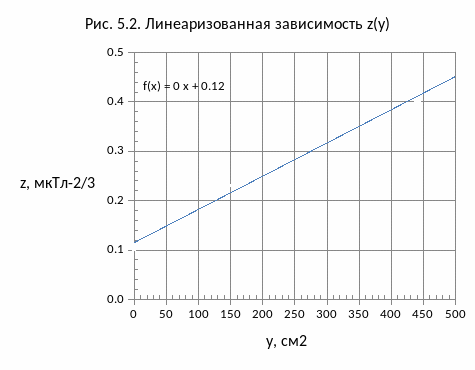
• Проведите по линейке экспериментальную прямую – так, чтобы она пересекла планки погрешностей всех экспериментальных точек и при этом прошла наиболее близко ко всем точкам. Образец показан на рисунке 5.2.

7. И змерьте параметры построенной прямой линии b и z₀.

Параметр z₀ – это ордината точки пересечения экспериментальной прямой линии с осью ординат. Параметр b – это угловой коэффициент прямой линии. Чтобы его измерить, выберите на экспериментальной прямой линии произвольную точку A (желательно, справа от всех экспериментальных точек) и определите её координаты 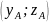. После этого b можно вычислить по формуле

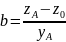. (5.2)

Для примера, показанного на рисунке 5.2, параметры экспериментальной прямой линии, следующие. Во-первых, линия пересекает ось ординат в точке 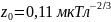. Во-вторых, выбрана точка A с координатами 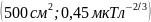, что даёт значение b, равное

.

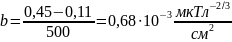Программа EXCEL выдаёт уравнение тренда: 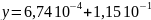, откуда следует, что .

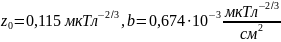8. Используя формулу (1.13)

,

определите значения магнитного момента витка p и радиуса витка R. Как указано выше, это – второй способ измерения p и R.

9. Оцените погрешности измерений (z₀) и (b), а затем погрешности измерений (p) и (R) вторым способом. Как это сделать, написано в пункте 6.

10. Запишите результаты измерения магнитного момента и радиуса витка вторым способом в виде:

.

.

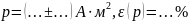11. Измерьте значение магнитного момента витка p первым способом, то есть на основе формулы (1.9) , и оцените погрешность измерения (p). После этого запишите результаты измерения магнитного момента и радиуса витка первым способом в виде:

.

.

12. Сравните результаты измерений R и p, полученные первым и вторым способами.

13. Сформулируйте выводы.