53 (076.5)

Л125

Министерство энергетики и угольной промышленности Украины

Севастопольский национальный университет ядерной энергии и промышленности

Лабораторный практикум по физике

Часть 3Б. Магнетизм

Методическое пособие по дисциплине

«Лабораторный практикум по физике»

Севастополь

2013

Оглавление

Работа 39. Изучение магнитного поля кругового тока	3
Работа 41. Измерение напряжённости магнитного поля Земли	17
Работа 42. Определение удельного заряда электрона	26
Работа 43. Построение петли гистерезиса методом Столетова	35
Рекомендуемая литература	45

Работа 38. Изучение магнитного поля кругового тока

В.В. Довгаленко, А.Г. Рипп

Цель работы

Исследовать зависимость магнитной индукции на оси кругового витка с током от расстояния до плоскости, в которой расположен виток.

1. Краткая теория

Проводник, по которому течёт электрический ток, создаёт вокруг себя магнитное поле. Это поле зависит от силы тока в проводнике, от формы проводника и от свойств среды, окружающей проводник. В данной лабораторной работе вам предлагается исследовать магнитное поле проводника, который имеет форму кольца и находится в воздухе. В дальнейшем этот проводник называется «виток».

Главной количественной характеристикой магнитного поля является векторная физическая величина, которая называется магнитной индукцией и обозначается буквой B. Магнитная индукция описывает магнитное поле в каждой его точке, так что она является функцией координат: . Зависимость магнитной индукции от силы тока в проводнике, создающем поле, и от формы проводника определяют следующие два закона.

• Закон Био-Савара-Лапласа.

• Принцип суперпозиции.

Закон Био-Савара-Лапласа утверждает, что каждый элементарный участок проводника (элемент тока) длиной d𝓁 и током I создаёт в вакууме магнитное поле, индукция которого dB на расстоянии r от элемента равна:

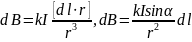. (1.1)

Э ти формулы поясняет рисунок 1.1.

На этом рисунке показан проводник с током I и элемент тока длиной d𝓁. Вектор d𝓵 направлен вдоль тока, а длина его равна длине элемента d𝓁. Вектор r начинается в элементе, а кончается в некоторой (произвольной) точке A. Иными словами, r – это радиус-вектор, определяющий положение точки A. Длина вектора r – это расстояние r от элемента до точки A. Вектор магнитной индукции dB в точке A направлен перпендикулярно плоскости чертежа, то есть плоскости, образованной векторами d𝓵 и r. Крестик в кружочке показывает, что вектор dB направлен за чертёж, то есть в сторону от наблюдателя. Угол между векторами d𝓵 и r обозначен буквой α. Буквой k в законе Био-Савара-Лапласа обозначена константа, равная

.

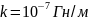Принцип суперпозиции состоит в том, что магнитная индукция B поля, созданного всем проводником, складывается в каждой точке поля из бесконечного числа малых слагаемых dB, каждое из которых – это магнитная индукция поля, созданного одним из элементов проводника: каждому элементу соответствует своё слагаемое dB. Сумма бесконечно малых – это интеграл, так что

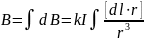. (1.2)

Значение интеграла в этой формуле зависит от формы проводника и от координат точки A.

Рассмотрим вычисление этого интеграла в случае, когда проводник представляет собой кольцо (виток), а точка A находится на оси витка – см. рисунок 1.2.

В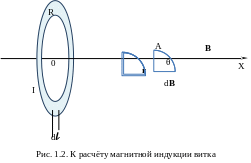 ыберем ось OX вдоль оси витка, а начало координат выберем в центре витка. Тогда координата x точки A – это расстояние от точки A до плоскости витка. Выберем один из элементов тока d𝓵 – например, внизу витка. Вектор d𝓵 направлен перпендикулярно плоскости рисунка, от наблюдателя. А так как радиус-вектор r, направленный из элемента в точку A, лежит в плоскости рисунка, то угол α между d𝓵 и r равен 90°, так что из (1.1) следует:

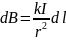. (1.3)

Согласно правилам вычисления векторного произведения, вектор 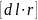направлен перпендикулярно каждому из векторов d𝓵 и r, так что вектор и определяемый им вектор dB лежат в плоскости рисунка. Прежде чем вычислять интеграл (1.2), заметим, что полная магнитная индукция B в точке A может быть направлена только вдоль оси OX, так что 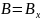. Это следует из условия симметрии. Данный факт облегчает вычисление интеграла (1.2), так как его можно записать в скалярной форме:

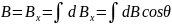. (1.4)

С учётом (1.3) из (1.4) следует:

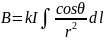. (1.5)

Из условия симметрии следует, что для всех элементов тока, а не только того – нижнего, который показан на рисунке 1.2, угол θ между вектором dB и осью OX – один и тот же. Кроме того, точка A равноудалена от всех точек витка, так что для всех элементов расстояние r одно и то же. Поэтому интеграл (1.5) легко вычисляется:

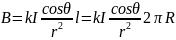. (1.6)

Из рисунка 1.2 видно, что 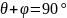, поэтому 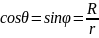. Кроме того, из теоремы Пифагора следует, что 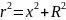. Таким образом,

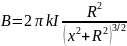. (1.7)

Эта формула определяет магнитное поле в вакууме. В среде это поле отличается от поля в вакууме, но если средой является воздух, то отличие несущественное. Важно, однако, что индукция магнитного поля, созданного витком, слишком мала, чтобы её можно было достаточно точно измерить приборами учебной лаборатории. Поэтому целесообразно вместо одного витка использовать несколько одинаковых, тесно прижатых друг к другу, изолированных витков тонкой проволоки, то есть тонкую катушку, которую будем в дальнейшем называть задающей катушкой. Считая, что все витки задающей катушки находятся в одном и том же месте, получим из принципа суперпозиции и формулы (1.7) следующее выражение для магнитной индукции на оси задающей катушки:

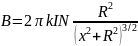, (1.8)

где N – число витков в задающей катушке.

Как один виток, так и вся задающая катушка – это магнитный диполь, аналогичный обычному постоянному магниту: с одной стороны у витка находится северный полюс, из него выходят линии магнитной индукции, а с другой стороны – южный полюс, куда линии индукции входят – см. рисунок 1.3.

К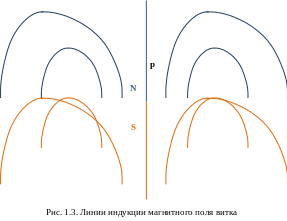 оличественной характеристикой магнитного диполя является дипольный момент p. Это – вектор, направленный перпендикулярно плоскости витков вдоль линий индукции, величина (модуль) дипольного момента одного витка равен произведению силы тока в витке на площадь витка: , а величина дипольного момента катушки в N раз больше. Если витки – круглые, то

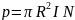, (1.9)

поэтому

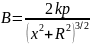. (1.10)

Задачей данной лабораторной работы является экспериментальная проверка этой формулы, точнее – зависимости магнитной индукции B на оси задающей катушки от расстояния x до плоскости катушки. И здесь есть две проблемы.

• Во-первых, надо придумать способ измерения магнитной индукции.

• Во-вторых, теоретическая зависимость B(x) – не линейная, поэтому её следует линеаризовать.

Как измерять магнитную индукцию, написано в следующем пункте. А здесь рассмотрим проблему линеаризации. Линеаризация означает переход от физических величин, зависящих друг от друга нелинейно, к двум другим величинам, которые связаны друг с другом простой линейной зависимостью.

Перепишем формулу (1.10) в следующем виде:

.

Возведём левую и правую часть этого равенства в степень :

.

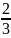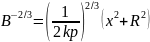А теперь сделаем замену переменных:

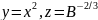. (1.11)

Новые переменные (вспомогательные физические величины) z и y связаны друг с другом линейной зависимостью:

, (1.12)

причём параметры этой зависимости определяются формулами:

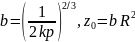. (1.13)

Проведя серию экспериментов по измерению магнитной индукции B в разных точках на оси задающей катушки, можно получить экспериментальную зависимость B(x), а из неё – используя формулы(1.11), экспериментальную зависимость z(y). Если на основании полученных результатов построить график зависимости z(y), то в случае правильности формулы (1.10) точки на графике должны выстроиться вдоль прямой линии.

Измерив параметры построенной прямой линии b и z₀, можно определить магнитный момент и радиус витка, так как из (1.13) следует:

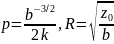. (1.14)

Эти же величины можно измерить и более просто. Радиус витка – прямым способом, а магнитный момент на основании формулы (1.9) 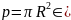. Этот способ измерения R и p будем называть первым, а способ, основанный на формулах (1.14), – вторым. Если результаты измерений радиуса витка и его магнитного момента, полученные первым и вторым способами, совпадут, то это даст основания считать правильными оба способа. Следовательно, это даст дополнительные аргументы в пользу правильности формулы (1.10).

2. Методика измерения магнитной индукции

В данной лабораторной работе предлагается способ измерения магнитной индукции, основанный на явлении электромагнитной индукции.

Это явление состоит в следующем. Если в какой-либо точке A в поле витка (задающей катушки¹) поместить маленькую (пробную) катушку, то при условии протекания по витку переменного тока в пробной катушке тоже возникает переменный ток. Объясняется это тем, что переменный ток в витке создаёт вокруг него переменное магнитное поле, а оно, в свою очередь, создаёт вокруг себя переменное электрическое поле. Электрическое поле действует на свободные электроны в проводе, намотанном на пробную катушку, в результате чего электроны приходят в движение, что и означает возникновение электрического тока.

Количественно описанное явление описывается законом электромагнитной индукции:

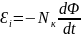, (2.1)

где Ɛ_i – ЭДС индукции (считается, что эта ЭДС и вызывает ток в пробной катушке), N_к – число витков провода в пробной катушке, Φ – магнитный поток через каждый виток пробной катушки (поток магнитной индукции), который связан с магнитной индукцией B и площадью каждого витка S_к формулой

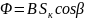. (2.2)

Угол β – это угол между нормалью к виткам пробной катушки и вектором B в точке расположения катушки (в точке A). Если ток в витке постоянный, то он создаёт стационарное магнитное поле (магнитостатическое), которое создаёт стационарный, то есть не изменяющийся с течением времени магнитный поток. Тогда производная 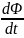равна нулю, в результате и ЭДС индукции равна нулю, так что никакого тока в пробной катушке не возникает. А вот если по витку протекает переменный ток, то 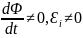, что и порождает электрический ток в пробной катушке, если она включена в какую-то замкнутую цепь. Знак «минус» в формуле (2.1) позволяет определить направление тока в катушке.

Переменный ток в витке может протекать по двум причинам.

• Причина 1: виток подключен к сети переменного тока.

• Причина 2: виток подключен к источнику постоянного тока, поэтому ток в нём постоянный – за исключением небольшого промежутка времени после подключения, когда ток в витке нарастает от нуля до постоянного (стационарного) значения. Этот промежуток времени называется временем установления, а его длительность обозначается обычно τ. В данной лабораторной работе реализована именно эта – вторая ситуация: виток подключен к источнику постоянного тока.

Силу тока в пробной катушке можно определить по закону Ома для замкнутой цепи:

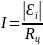, (2.3)

где R_ц – сопротивление цепи. С учётом формул (2.1) и (2.2) получим:

.

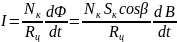Для того чтобы ток в пробной катушке был максимально возможным, её надо устанавливать так, чтобы ось катушки была направлена вдоль линий магнитной индукции – в этом случае 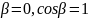и тогда

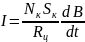. (2.4)

По определению силы тока, 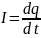, где dq – это заряд, прошедший по проводнику за время dt. При этом из (2.4) следует:

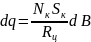. (2.5)

Интегрирование этого равенства даёт:

.

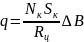Здесь q – это заряд, прошедший через пробную катушку за время установления τ, а B – это изменение магнитной индукции за время установления, то есть разница 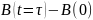. В начальный момент времени сила тока в витке ещё равна нулю, а следовательно, и никакого магнитного поля нет, так что 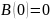. В конце времени установления магнитная индукция достигает стационарного значения B, которое в дальнейшем больше не изменяется. Таким образом, 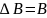и в результате

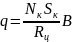. (2.6)

Из этой формулы видно, что для измерения магнитной индукции достаточно измерить заряд q, прошедший через пробную катушку за время установления. Разумеется, при этом надо знать параметры катушки 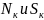и сопротивление цепи R_ц, в которую включена катушка.

Для измерения заряда q в данной лабораторной работе предлагается использовать прибор, который называется баллистическим гальванометром. Он соединяется с пробной катушкой и представляет собою всю её внешнюю цепь, поэтому R_ц – это сумма сопротивлений катушки и гальванометра. Всякий гальванометр – это прибор, реагирующий на протекание электрического тока. Особенностью баллистического гальванометра является его повышенная инерционность. Это означает следующее: время установления очень мало, так что электрический ток в пробной катушке течёт очень недолго, но баллистический гальванометр реагирует на этот ток замедленно – ток уже прекратился, а стрелка гальванометра только-только начинает отклоняться. Отклонившись до некоторого значения, она – опять замедленно – возвращается в исходное нулевое положение. Но при этом оказывается так, что максимальное отклонение стрелки баллистического гальванометра пропорционально заряду q, прошедшему через него за время протекания тока. Так как в гальванометре протекает тот же самый ток, что и в пробной катушке, то время протекания тока через гальванометр равно времени установления τ, а заряд, прошедший через гальванометр, равен заряду q, прошедшему за время установления через катушку.

Итак, обозначив буквой α максимальное отклонение стрелки гальванометра при замыкании цепи витка, можно записать:

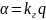, (2.7)

где коэффициент пропорциональности k_г называется чувствительностью гальванометра.

Из (2.7) и (2.6) следует формула, определяющая метод косвенного измерения магнитной индукции:

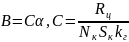. (2.8)

Для измерения коэффициента C не обязательно измерять параметры пробной катушки, сопротивление цепи катушки и чувствительность гальванометра – можно поступить проще. Из формулы (1.7) следует, что магнитная индукция в центре витка равна:

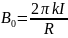. (2.9)

Применение формулы (2.8) даёт:

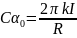, (2.10)

где α₀ – максимальное отклонение стрелки гальванометра при помещении пробной катушки в центре витка. Из формулы (2.10) следует, что значение C можно узнать, измерив только α₀, силу тока в витке I и радиус витка R. Однако целесообразно сначала проверить, правильна ли формула (2.10). Это проще всего сделать так. Из формулы (2.10) следует, что значение α₀ прямо пропорционально силе тока в витке:

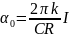. (2.11)

Поэтому следует провести серию измерений α₀ при различных значениях силы тока I в витке, а затем на основании результатов измерений построить график зависимости α₀(I). Если точки на этом графике выстроятся вдоль прямой линии, проходящей через начало координат, то данный факт будет подтверждением формулы (2.11). Тогда, измерив угловой коэффициент E построенной прямой линии, можно узнать значение C:

. (2.12)