2.5. Расчет маховика

Крутящий момент двигателя является величиной постоянной, в то время как момент сопротивления вращению компрессора меняется в соответствии с диаграммой тангенциальных сил. Вследствие этого для нормальной работы компрессора необходимо аккумулирование механической энергии, достигае­мой установкой маховика, массивной муфты и т.д. Отсутствие их привело бы к вибрации компрессора и пульсации тока в сети питания электродвигателя.

Если момент сопротивления вращению меньше крутящего момента двигателя, маховик накапливает энергию и отдает ее, когда момент сопротивления вращению становится больше крутящего момента двигателя. При накапливании энергии маховик разгоняется, т.е. увеличивается его угловая скорость до ω_max, а при расходовании накопленной энергии угловая скорость уменьшается до ω_min. Расчет маховика сводится к определению его массы по избыточной работе, соответствующей наибольшей избыточной площадке на диаграмме тангенциальных сил и допускаемому значению степени неравномерности вращения:

Необходимый маховый момент инерции маховика (в кг ∙ м²)

где ΔА - максимальная избыточная работа, которую должен аккумулировать маховик, Дж;

δ - степень неравномерности вращения;

ω_ср, - средняя угловая скорость (ω_ср = 2πn).

Максимальная избыточная работа, соответствующая наибольшей избыточной площадке на диаграмме тангенциальных сил:

где f_max - площадь избыточной площади на диаграмме тангенциальных сил, мм²;

m_l - масштаб длин m_l = l/2πr , в котором l - длина диаграммы, мм; r - радиус кривошипа, м;

m_р - масштаб сил, мм/Н.

Масса маховика, достаточная для обеспечения допускаемой степени неравномерности (в кг):

где r_max - радиус инерции маховика, равный среднему радиусу обода маховика (принимаем конструктивно), м.

Конструктивно принимаются размеры маховика: наружный и внутренний диаметры, ширина и толщина обода.

В принятой конструкции маховика, муфты степень неравномерности со­ставит:

2.7 Уравновешивание

При работе компрессора на опоры коленчатого вала, корпус передаются неуравновешенные силы и моменты, вызывая вибрацию, дополнительные нагрузки на детали компрессора. Анализ сил, действующих в компрессоре (рисунок 3), показывает, что неуравновешенными в многорядных компрессорах могут быть силы инерции возвратно-поступательно и вращательно - движущихся масс, а также моменты от этих сил. При проектировании компрессоров путем выбора схем расположения кривошипов коленчатого вала и цилиндров, подбора противовесов стремятся обеспечить условия, при которых суммарные силы инерции, а также моменты этих сил были бы равны нулю. Полное уравновешивание из-за значительного усложнения конструкции практически неосуществимо.

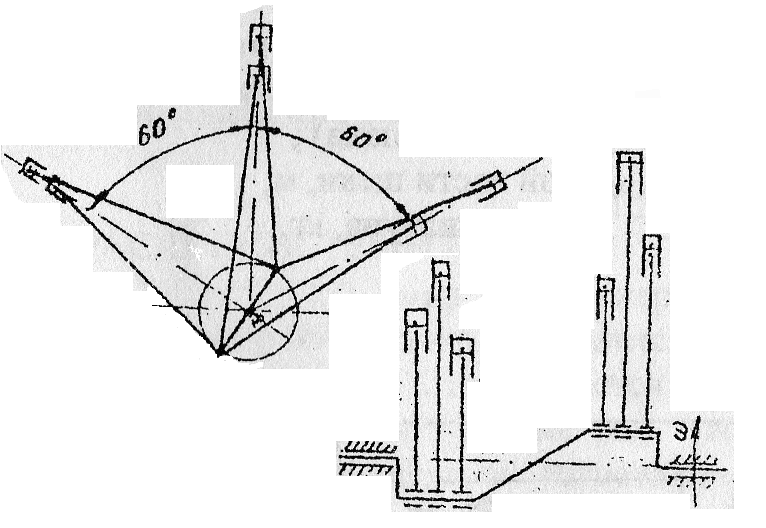
Рисунок 9 - Компоновка (шестирядный угловой компрессор с двумя коленами вала под углом 180°, угол между рядами 60°).

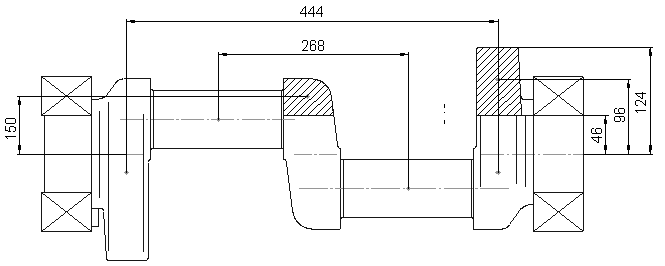
Рисунок 10 – Вал компрессора.

Силы инерции первого порядка взаимно уравновешены. Силы инерции второго порядка не уравновешиваются. Силы инерции неуравновешенных вращающихся масс взаимно уравновешены. Момент сил инерции первого порядка, действующий в плоскости колен:

.

Он может быть уравновешен двумя противовесами массой, приведенной к радиусу кривошипа :

.

Масса неуравновешенной части щеки:

m_щ = V_щ ∙ ρ = 0,00015 ∙7850 = 1,18,

где - объем неуравновешенной части щеки;

ρ - плотность материала противовеса (для чугуна 7850), кг/м³.

Полная величина неуравновешенной массы, приведенной к радиусу кри­вошипа:

m_R= i ∙ m_ш.ш.+ 2 ∙ m_щ∙ + i ∙ m_ш.вр. =

= 5,5 + 1,18 ∙ + 3 ∙ 2,12∙= 13,82,

где i - число шатунов на шатунной шейке;

m_ш.ш - масса шатунной шейки, приходящаяся на один шатун, кг;

m_щ - масса неуравновешенных частей щек вала, кг (принимают одинако­выми на обоих концах шатунной шейки и находят приближенно, как для прямоугольного параллелепипеда);

Момент сил инерции второго порядка не возникают. Момент сил инерции неуравновешенных вращающихся масс, действующий в плоскости колен, постоянный по величине во всех положениях вала

M_R = m_R ∙ r ∙ ω² ∙ a = 20,3 ∙ 0,041 ∙ ∙ 0,226 = 4415.

Он может быть уравновешен двумя противовесами массой, приведенной к радиусу кривошипа

m''_пр= m_R ∙ а/в = 13,87 ∙ 0,268/0,444= = 8,4,

создающими момент, равный по величине, но противоположно направленный.

Общая масса противовеса:

Σm_пр = m'_пр + m''_пр = 14,3 + 8,4 = 22,7.

Масса противовеса будет равняться:

m_пр = Σm_пр ∙ = 22,7 ∙ = 9,9

где r_пр - радиус инерции противовеса, который определяем по принимаемым размерам противовеса как расстояние от центра массы противовеса до оси вращения.

Угол габарита противовеса:

где h_ср, - средняя толщина противовеса, м.

Сила инерции противовеса:

J_пр = m_пр ∙ r_пр ∙ ω² = 9,9 ∙ 0,094 ∙ = 9559

Сила инерции неуравновешенной части щеки:

J_щ = 2 ∙ m_щ ∙ r_щ ∙ ω² = 1,18 ∙ 0,068 ∙ = 830,5.

Силу инерции противовеса и силу инерции неуравновешенной части щеки необходимо учитывать при расчете коленчатого вала на прочность и жест­кость.