Ответы на вопросы по дисциплине "Основы менеджмента качества", "Квалиметрия"

Вопросы:

1.Виды случайных величин в управлении качеством

2.Применение биномиального, гипергеометрического законов распределения в управлении качеством

3.Применение в управлении качеством закона распределения Пуассона

4.Применение регрессионного анализа в управлении качеством

5.Применение корреляционного анализа в управлении качеством

6.Проверка статистических гипотез в управлении качеством

7.Приемочный контроль. Виды планов статистического контроля

8.Числовые характеристики одноступенчатых планов статистического контроля

9.Числовые характеристики двухступенчатых планов статистического контроля

10.Стандарты статистического приемочного контроля

Ответы:

1. Непрерывные и дискретные случайные величины, числовые характеристики случайных величин

Непрерывной случайной величиной (СВ) называется величина, которая при испытании может принять любое значение из заданного диапазона. В окрестности этого диапазона зададим бесконечно малый интервал значений [x, x+dx] и обозначим dP вероятность попадания СВ в этот интервал.

Введем понятие дифференциальной функции распределения w(x) через вероятность dP с помощью соотношения

(1.9)

Введем также понятие интегральной функции распределения

(1.10)

Физический смысл этого соотношения означает вероятность попадания СВ в диапазон значений от - до x. Впредь (если это не будет оговорено дополнительно), употребляя термин распределение СВ, будем иметь в виду дифференциальную функцию распределения.

Функция распределения СВ дает полное статистическое описание этой величины и позволяет определить ее числовые характеристики . Наиболее существенными из них являются следующие.

Среднее значение (математическое ожидание, первый начальный момент) непрерывной СВ вычисляется по формуле

(1.11)

Здесь символ обозначает операцию усреднения.

Дисперсия или второй центральный момент имеет вид

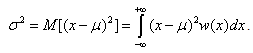(1.12)

При этом величина

(1.13)

носит специальное название – среднеквадратическое (стандартное) отклонение случайной величины от среднего значения. Для дисперсии случайной величины легко доказывается важная в дальнейшем формула

(1.14)

Медианой называется значение , для которого выполняется соотношение

(1.15)

В отличие от непрерывных дискретные СВ могут принимать лишь избранные значения на числовой оси. Примерами таких величин являются показания цифрового измерительного прибора или число бракованных изделий m при выборочном контроле партии объемом n изделий. Распределение дискретной СВ представляет собой линейчатую функцию. Каждое значение этой функции является вероятностью того, что рассматриваемая СВ будет обладать конкретной величиной. Аналог интегрального распределения в случае дискретных СВ находится суммированием дискретного распределения.

Среднее значение дискретной СВ вычисляется по формуле

(1.16)

Дисперсия дискретной СВ вычисляется по формуле

(1.17)

Здесь - значение случайной величины, - ее вероятность.