Національний університет біоресурсів і

природокористування України

Кафедра вищої математики

ім М.П.Кравчука

ІНДИВІДУАЛЬНІ ЗАВДАННЯ

З „ЛІНІЙНОЇ АЛГЕБРИ”

для студентів ННІ бізнесу

Київ – 2012

УДК 378.022:51

Методичні вказівки містять довідковий матеріал, необхідний для самопідготовки студентів по темах „Лінійна алгебра”, завдання для самопідготовки, тести.

Рекомендовано вченою радою природничо-гуманітарного ННІ, протокол № 2, від 20 жовтня 2011 року.

Укладач: Іванова Ю.І., канд. фіз.-матем. наук, доцент,

Ружило М.Я., старший викладач.

Рецензенти: Мейш В.Ф., професор, Ковтун І.І., доцент.

Індивідуальні завдання

з „ЛІНІЙНОЇ АЛГЕБРИ”

для студентів ННІ бізнесу

Київ – 2012

ІНДИВІДУАЛЬНІ ЗАВДАННЯ по темі

„ЛІНІЙНА АЛГЕБРА”

Варіант 1

1. Розв’язати рівняння. Зробити перевірку. .

2. Обчислити визначник

.

3. Знайти значення матричного многочлена , якщо Е – одинична матриця 3-го порядку,

.

4. Знайти добутки CD та DC, якщо

; .

Яку матрицю А потрібно відняти від матриці DC, щоб отримати одиничну матрицю?

5. Розв’язати матричне рівняння відносно квадратної матриці Y 3-го порядку AYB=C, якщо

; ; .

6. Розв’язати систему лінійних рівнянь a) за формулами Крамера;

б) матричним методом.

7. Розв’язати систему рівнянь методом Гаусса:

.

8. Знайти ранг матриці .

Варіант 2

1. Знайти площу трикутника з вершинами A(2; 3), B(4; –1), C(6; 5).

Вказівка. Площа трикутника з вершинами A(x₁; y₁), B(x₂; y₂), C(x₃; y₃).

.

2. Обчислити визначник Вандермонда накопиченням нулів у рядку чи у стовпці

.

3. Знайти: a) 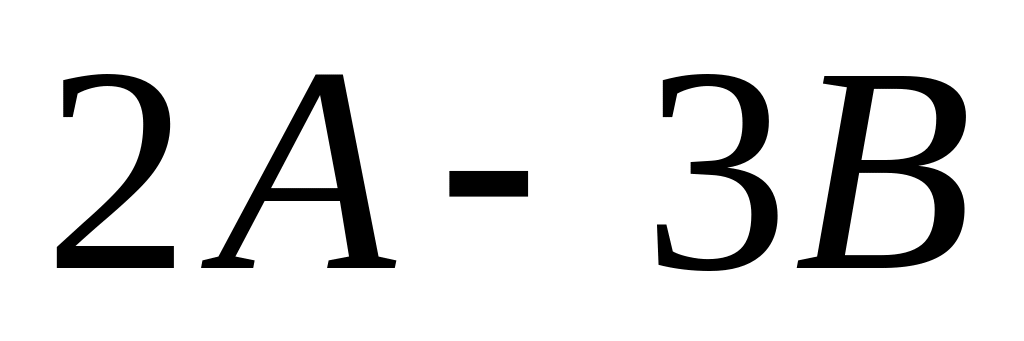; б) , якщо

; = ; = .

4. Нехай

= ; = .

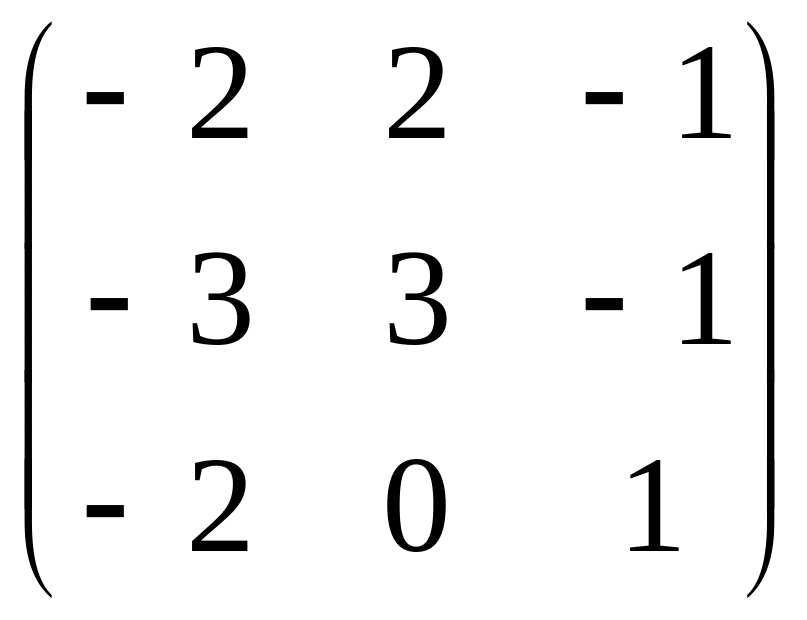Знайти добутки ( ) та ( ) .

5. Розв’язати матричне рівняння, зробити перевірку.

.

6. Розв’язати систему лінійних рівнянь а) за формулами Крамера;

б) матричним методом.

7. Розв’язати систему рівнянь методом Гаусса:

.

8. Знайти ранг матриці .

Варіант 3

1. Не розкриваючи визначника, довести тотожність

.

Вказівка. Привести визначник до трикутного вигляду (ІІр – Ір; ІІІр – Ір; ІІІр – ІІр), а такий визначник дорівнює добутку його діагональних елементів.

2. Обчислити визначник накопиченням нулів у рядку чи у стовпці

.

3. Обчислити Р(А)=А²–3А+5Е, якщо Е – одинична матриця 3-го порядку,

.

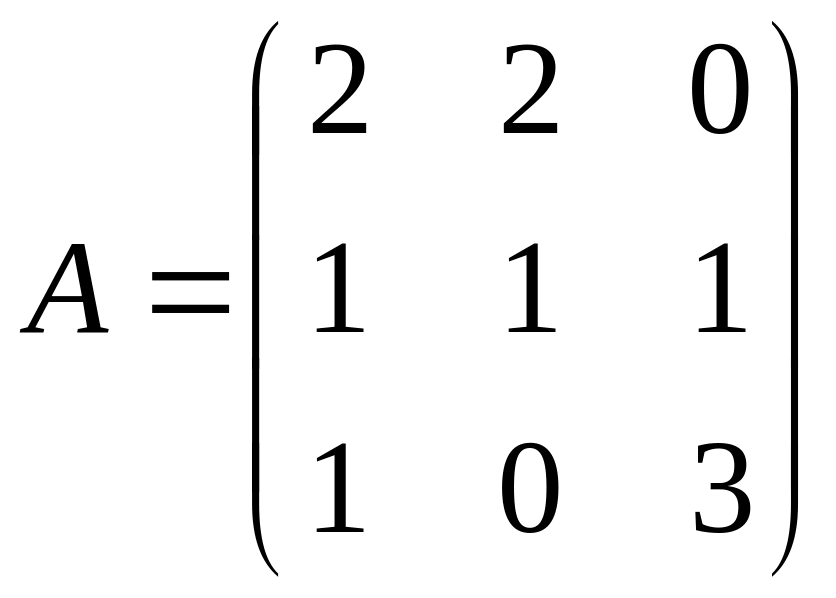4. Знайти матрицю С=АВ–ВА, якщо

; .

Яку матрицю D потрібно додати до матриці С^Т, щоб дістати одиничну матрицю?

5. Розв’язати матричне рівняння, зробити перевірку.

.

6. Розв’язати систему лінійних рівнянь a) за формулами Крамера;

б) матричним методом.

7. Визначити, при яких значеннях а та b система рівнянь a) має єдиний розв’язок (визначена); б) не має розв’язків (несумісна).

8. Знайти ранг матриці .

Варіант 4

1. Користуючись властивостями визначників, обчислити визначник

2. Обчислити визначник, зробивши найбільше нулів у рядку чи у стовпці

.

3. Знайти значення матричного многочлена F(A)= – 3A²+3A – E, якщо Е – одинична матриця 3-го порядку,

.

4. Нехай задано матриці

та .

Знайти (якщо це можливо) АВ; ВА; А^ТВ^Т; В^ТА^Т.

Якщо операція множення матриць у деяких випадках неможлива, пояснити чому.

5. Розв’язати матричне рівняння та зробити перевірку

.

6. Розв’язати систему лінійних рівнянь a) за формулами Крамера;

б) матричним методом.

7. Розв’язати систему рівнянь методом Гаусса:

.

8. Знайти ранг матриці .

Варіант 5

1. Користуючись властивостями визначників, обчислити визначник

.

Вказівка. До 1-го стовпця додати 2-ий та 3-ій.

2. Знайти члени визначника, які містять х⁴ та х³,

.

3. Знайти , якщо Е – одинична матриця 3-го порядку,

.

4. Задано матриці

та .

а). Знайти (якщо це можливо) АВ; ВА; А^ТВ^Т; В^ТА^Т.

б). Чому дорівнюють визначники матриць АВ та ВА?

5. Розв’язати матричне рівняння АХВ=С, якщо

; ; .

Зробити перевірку.

6. Розв’язати систему лінійних рівнянь a) за формулами Крамера;

б) матричним методом.

7. Розв’язати систему рівнянь методом Гаусса:

.

8. Знайти ранг матриці .

Варіант 6

1. Знайти х із рівняння

=0.

Зробити перевірку.

2. Обчислити визначник

.

3. Показати, що матриця –кососиметрична, якщо

= ; = .

Зауваження. Квадратна матриця називається кососиметричною, якщо при транспонуванні вона змінює свій знак.

4. Задано матриці

= та = ,

Знайти добуток . Чи можна помножити матрицю на матрицю ? Яку матрицю потрібно відняти від матриці , щоб дістати одиничну матрицю?

5. Розв’язати матричне рівняння, зробити перевірку.

= .

6. Розв’язати систему лінійних рівнянь а) за формулами Крамера;

б) матричним методом.

7. Визначити, при яких значеннях і 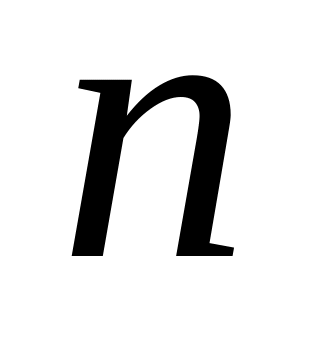система рівнянь а) має єдиний розв’язок; б) не має розв’язків.

8. Знайти ранг матриці .

Варіант 7

1. Не розкриваючи визначника, довести справедливість рівності

.

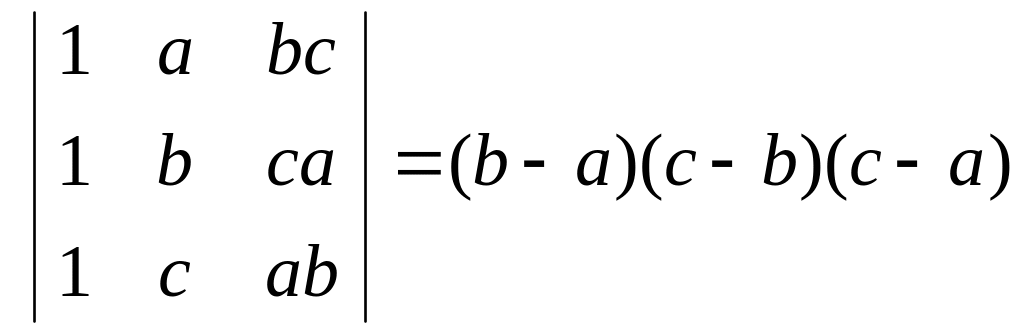Вказівка. Привести визначник до трикутного вигляду (ІІІр.–ІІр.; ІІр.–Ір.; винести спільні множники за знак визначника; ІІІр.–ІІр.). Отриманий визначник дорівнює добутку елементів, які стоять на головній діагоналі.

2. Розв’язати рівняння, ліва частина якого записана у вигляді визначника,

.

Вказівка. Ір.–ІІр.; розкласти за елементами 1-го рядка;

ІІр.–ІІІр.; розкласти за елементами 2-го рядка.

3. Знайти , якщо Е – одинична матриця 3-го порядку,

.

4. Показати, що матриця В – ортогональна, якщо

.

Зауваження. Квадратна матриця А називається ортогональною, якщо виконується умова АА^Т=Е, або А^Т=А^–1.