4. Проаналізуйте ризик захворювання шизофренією у родичів хворих та зробіть висновок.

Коефіцієнти конкордантності допомагають визначити ризик захворюваності для різних категорій родичів. Наприклад, якщо для сібсів конкордантність по шизофренії складає 10%, можна вважати, що ризик захворювання шизофренією у людини, що має брата або сестру, які страждають на це захворювання, складе 1 на 10 випадків. Як правило, конкордантність для родичів порівнюється з тією, що зустрічається хвороби в популяції. Наприклад, якщо було виявлено, що захворюваність шизофренією для родичів першого ступеня спорідненості складає 10%, а в популяції зустрічається цієї хвороби усього 1%, можна говорити про більш високий ризик захворювання у родичів. У таблиці 3. приведені частоти захворюваності шизофренією для різних категорій родичів.

Таблиця 3

Ризик захворювання шизофренією у родичів хворих

Спорідненість з хворим	Коефіцієнт спорідненості	Частота захворюваності шизофренією (%)
Неродичи	0,00	0,85
Звідні сібси	0,00	1,80
Полусібси	0,25	3,20
Сібси	0,50	7,0-15,0
Батьки	0,50	5,0-10,3
Діти	0,50	7,0-16,4
Онуки	0,25	3,0-4,3
Племінники або племінниці	0,25	1,8-3,9
Двоюрідні брати, сестри	0,125	1,8-2,0

Зіставлення оцінок конкордантності МЗ і ДЗ близнюків дає можливість оцінити долю впливу спадкових чинників на варіативну досліджуваної ознаки, тобто коефіцієнт наслідуваності h2. Для цього можна скористатися формулою Хольцингера:

h₂(100 – 50) = 0,5.

Отже, в наведеному прикладі коефіцієнт наслідуваності (у широкому значенні слова) дорівнює 0,5.

Висновок:

5. Розгляньте приклад обчислення коефіцієнта кореляції та зробіть висновок

Можна, наприклад, поставити питання, чи існує зв'язок між двома кількісними ознаками у людини, наприклад, між густиною волосся і ростом. Тут можливі три варіанти: 1) чим густіше волосся, тим вище ріст, 2) чим густіше волосся, тим ріст нижчий, 3) цих ознаки ніяк не пов'язані між собою. Якщо вірне останнє твердження, то ми б сказали, що ці ознаки не корелюють. У першому випадку можна говорити про позитивну кореляцію, в другому - про негативну. Основний принцип підрахунку кореляції полягає в наступному. Візьмемо, наприклад, такі ознаки, як ріст людини і його вагу. Припустимо, що у групи індивідів ми провели відповідні виміри і занесли дані в таблицю (таблиця. 4 ).

Таблиця 4

Приклад даних для обчислення коефіцієнта кореляції між ростом і вагою

Індивід	Ріст(см)	Відхилення від середнього	Вага (кг)	Відхилення від середнього
А	165	-7	58	-14
Б	168	-4	64	-8
В	170	-2	68	-4
Г	174	+2	76	+4
Д	176	+4	80	+8
Е	179	+7	86	+14
Середнє	172		72

Розглядаючи таблицю, ми можемо помітити, що відхилення росту кожної людини від середньої величини прямо пропорційно таким же відхиленням, що відносяться до його ваги. В даному прикладі ріст і вага демонструють максимальну позитивну кореляцію, величина якої дорівнює +1,0. Якщо ми розташуємо значення в одному із стовпців в зворотному порядку, то отримаємо негативну кореляцію з величиною коефіцієнта, рівною, - 1,0. Якщо ми у випадковому порядку перемішаємо усі цифри, то кореляція буде близька до 0.

Графічно позитивна кореляція між двома величинами може бути представлена у вигляді лінії з позитивним нахилом (рис.1а), при цьому на осях Х і Y відкладаються значення корельованих ознак; негативна кореляція може бути представлена у вигляді лінії з негативним нахилом (рис. 1б), відсутність кореляції виражається у відсутності нахилу відповідної лінії (рис. 1в). Таким чином, величина кореляції говорить нам про те, наскільки відхилення від середньої однієї величини співпадають з відхиленнями інший. (Нагадаємо, що усе, що пов'язано з відхиленнями від середніх величин – це область, близька до проблем варіативної і вимірів дисперсії.) Однонаправлений характер відхилень призводить до виникнення високої позитивної кореляції. В той же час величина коефіцієнта кореляції не несе ніякої інформації про абсолютні величини двох ознак. Поглянувши на таблицю, ми переконаємося, що в колонках цифр абсолютні значення росту і ваги відрізняються приблизно на сто одиниць. Дві змінні можуть ідеально корелювати один з одною, навіть якщо кожне значення однієї значно більше, чим кожне значення іншої. Ця обставина має безпосереднє відношення до розуміння значень кореляцій в оцінці схожості між родичами.

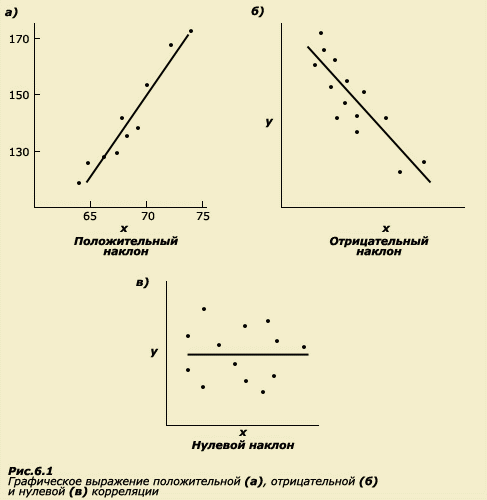
Рис. 1. Графічне вираження позитивної, негативної та нульової кореляції.

Висновок: