Министерство образования и науки

Филиал федерального государственного

Бюджетного образовательного учреждения

Высшего профессионального образования

«Камская государственная инженерно-экономическая академия»

в г. Чистополе

МЕХАНИКА

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Методические указания для контрольных работ

заочное обучение

Чистополь

2012 год.

УДК 53

Механика. Молекулярная физика и термодинамика: Методические указания для выполнению контрольных работ по курсу физика /Составитель С.Г.Смирнов.-Чистополь, филиал ИНЭКА. 2012.-51с.

Методические указания предназначены в помощь студентам при выполнении контрольных работ. В них изложены все необходимые сведения из теории. Приводится список литературы.

Список лит. 4 назв.

Рецензент: доцент: к.т.н. Э.Г.Сайфуллин.

Печатается по решению научно-методического совета филиала Камской государственной инженерно-экономической академии от «______»___________________2012 года.

© Камская государственная инженерно-экономическая академия, 2012 г.

Литература

1. Савельев И.В. Курс общей физики. Т. I – М.: Наука, 1982

2. Савельев И.В. Курс физики. Т. I – М.: Наука, 1989.

3. Детлаф А.А., Яворский В.М. Курс физики. – М.: Высшая школа, 1989.

4. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Высшая школа, 1981.

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ

В данной брошюре приведено контрольное задание по разделу «Физические основы механики» и «Молекулярная физика и термодинамика»

Студенты должны решить из таблицы восемь задач того варианта, номер которого совпадает с последней цифрой его шифра.

Перед выполнением контрольной работы студент должен проработать соответствующий материал по учебным пособиям разобрать примеры решения типовых задач, приведенных в данной брошюре и задачниках каждое контрольное задание выполняется в тонкой школьной тетради. На лицевой стороне обложки приводятся сведения о студенте: фамилия, имя, отчество, факультет, шифр, группа; для иногородних – почтовый адрес. Необходимо также указать номер контрольного задания.

Условия задач в контрольных работах переписываются полностью без сокращений. Для замечаний преподавателя нужно оставлять поле и интервалы между задачами. В конце контрольной работы необходимо указать, каким учебным пособием пользовался студент (название учебника, автор, год издания).

Если контрольная работа не зачтена при рецензировании, ее следует направлять повторно на проверку после исправления ошибок.

Решения задач должны сопровождаться краткими, но исчерпывающими объяснениями, раскрывающими физический смысл использованных формул. Решения задач рекомендуется выполнять в следующей последовательности:

1. Ввести буквенные обозначения физических величин, если это не сделано в условии задачи. Выбрать систему отсчета.

2. Сделать (если это необходимо) чертеж, поясняющий содержание задачи.

3. Сформулировать физические законы, на которых базируется решение задачи.

4. Составить уравнение или систему уравнений, решая которую, можно найти искомую величины.

5. Решить уравнения в общем виде и получить расчетную формулу, в левой части которой стоит искомая величина, а в правой – величины, данные в условиях задачи.

6. Произвести вычисления. Для этого необходимо перевести все значения величин в одну систему единиц – СИ, а затем подставить их в расчетную формулу и выполнить вычисления. При решении задач, как правило, достаточно точности в 2…3 значащие цифры.

Студент обязан сдать на проверку выполненную им заочно контрольную работу до или после прибытия на сессию. Зачет по контрольной работе принимается преподавателем в процессе собеседования по предварительно проверенной и отрецензированной работе.

К экзамену студент допускается только после получения зачета по контрольным работам.

Механика

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ

1. Кинематическое уравнение движения материальной точки вдоль оси х:

х = ƒ (t),

где ƒ (t) – некоторая функция времени.

2. Средняя скорость

3. Средняя путевая скорость

где ΔS – путь, пройденный точкой за интервал времени Δt.

4. Мгновенная скорость

5. Среднее ускорение

6. Мгновенное ускорение

7. Кинематическое уравнение движения материальной точки по окружности

φ = f(t), r = R = const

8. Угловая скорость

9. Угловое ускорение

10. Связь между линейными и угловыми величинами, характеризующими движение точки по окружности.

, , ,

где υ – линейная скорость; и – тангенциальное и нормальное ускорение; ω – угловая скорость; β – угловое ускорение; R – радиус окружности.

11. Полное ускорение

или

12. Угол между полным и нормальным ускорениями

13. Кинематическое уравнение гармонических колебаний материальной точки

где х – смещение; А – амплитуда колебаний; ω – круговая частота; φ – начальная фаза.

14. Скорость и ускорение материальной точки, совершающей гармонические колебания

15. Сложение гармонических колебаний одного направления и одинаковой частоты:

а) амплитуда результирующего колебания

;

б) начальная фаза результирующего колебания

16. Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях ( , )

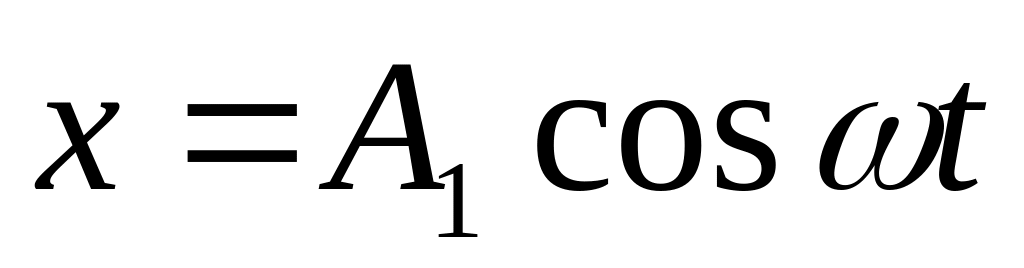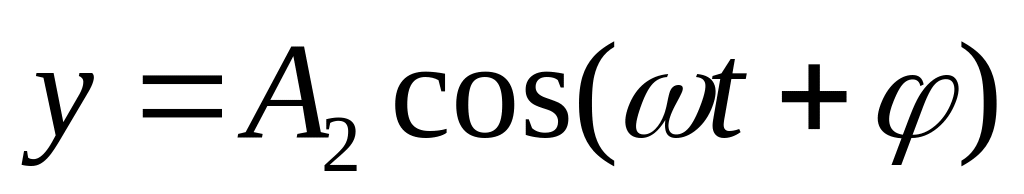а) у = (А₂/А₁)·х (если разность фаз φ = 0);

б) у = - (А₂/А₁)·х (если разность фаз φ = ± π/2);

в) х²/А₁² + у²/А₂² = 1 (если разность фаз φ равна ± π/2)

17. Уравнение плоской бегущей волны

,

где у – смещение любой из точек среды с координатой х в момент t; υ – скорость распространения колебаний в среде.

18. Связь разности фаз Δφ колебаний с расстоянием между точками среды, отсчитанным в направлении распространения колебаний:

где λ – длина волны.

19. Импульс материальной точки массой m, движущейся поступательно со скоростью

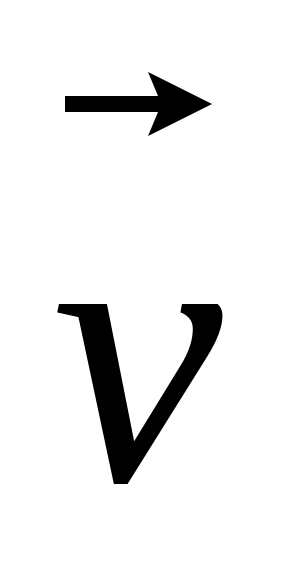
20. Второй закон Ньютона

где - сила, действующая на тело.

21. Силы, рассматриваемые в механике:

а) сила упругости

,

где k – коэффициент упругости (в случае пружины – жесткость); х – абсолютная деформация;

б) сила тяжести

в) сила гравитационного взаимодействия

,

где G – гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки);

г) сила трения (скольжения)

где f – коэффициент трения; N – нормального давления.

22. Закон сохранения импульса

или для двух тел (i = 2)

где и - скорости тел в момент, принятый за начальный;

и - скорости тел в момент времени, принятый за конечный

23. Кинетическая энергия тела, движущегося поступательно.

или

24. Потенциальная энергия:

а) упруго – деформированной пружины

где k – коэффициент жесткости пружины; х – абсолютная деформация:

б) гравитационного взаимодействия

где G – гравитационная постоянная; m₁ и m₂ – массы взаимодействующих тел; r – расстояние между телами (тела рассматриваются как материальные точки):

в) тела, находящегося в однородном поле силы тяжести,

где g – ускорение свободного падения; h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h « R, где R – радиус Земли).

25. Закон сохранения механической энергии:

26. Работа А, совершаемая внешними силами:

27. Основное уравнение динамики, вращательного движения относительно неподвижной оси:

где - результирующий момент внешних сил относительно оси z, действующих на тело; - угловое ускорение; - момент инерции тела относительно оси вращения.

28. Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:

а) стержня длиной l относительно оси, перпендикулярной стержню

;

б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра)

,

где R – радиус обруча (цилиндра);

в) диска радиусом R относительно оси, перпендикулярной плоскости диска,

29. Момент импульса тела, вращающегося относительно неподвижной оси z:

где - угловая скорость тела.

30. Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси

где и - моменты инерции системы тел и угловые скорости вращения в моменты времени, принятые за начальный и конечный.

31. Кинетическая энергия тела, вращающегося вокруг неподвижной оси:

или