Глава 7. Логарифмические неравенства

Определение: Неравенство, содержащее переменную только под знаком логарифма, называется логарифмическим.

При решении логарифмических неравенств следует помнить, что логарифмическая функция у= log_аx является возрастающей при а  1 и убывающей при 0  а  1. Поэтому из неравенства log_ax  log_ay следует, что х  у, если а  1, и х  у, если 0  а  1. При потенцировании обеих частей неравенства по основанию а знак неравенства сохраняется прежним, если а  1, и изменяется на противоположный, если 0  а  1. При решении логарифмических неравенств следует помнить о том, что областью определения логарифмической функции является множество положительных чисел.

ПРИМЕРЫ. Решить неравенства:

а) log₅(2x – 1)  2

Решение. Заметив, что 2 = log₅25, перепишем неравенство в виде:

log₅(2x – 1)  log₅25.

Учитывая, что неравенство имеет смысл при 2х – 1  0 (область определения логарифмической функции множество всех положительных чисел), и потенцируя обе части неравенства по основанию а = 5  1, придем к системе, равносильной данному неравенству:

х  13.

Ответ: (13;+).

б) lg(x – 1) +lg(x – 2) < lg(x+ 2)

Решение. Заменим в левой части уравнения сумму логарифмов логарифмом произведения.

lg(x – 1)(x – 2) < lg(x + 2).

Так как функция y = lg t возрастающая (а = 10, а > 1) и D(log) = R₊, то данное неравенство равносильно системе неравенств:

Решим отдельно второе неравенство методом интервалов:

х² – 4х  0;

х(х – 4)  0;

х(х – 4) =0;

х = 0 или х – 4 = 0

х = 4

+ – +

  

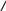
0 2 4 х

х  (0; 4), но х  2, поэтому х  (2; 4).

Ответ: (2; 4) или 2  х  4.

в) log₂²x – log₂x  6.

Решение. log₂²x – log₂x – 6  0.

Так как логарифмы существуют только для положительных чисел, утверждаем х  0.

Сделаем замену переменной t = log₂x, получим

t² – t – 6  0; решим неравенство методом интервалов:

t² – t – 6 = 0;

t₁ = – 2; t₂ = 3.

+ – +

 

– 2 3 t

– 2  t  3.

Переходим к исходной переменной:

• 2  log₂x  3.

Заметим, что 3 = log₂8 и –2 = log₂ , получим:

log₂  log₂х  log₂8.

Учитывая, что функция y = log₂t возрастающая и D(log) = R₊, получим систему неравенств:

Ответ: [ ;8].

Глава 8. Тригонометрические функции числового аргумента

8.1. Углы и их измерение

Определение: Фигура, состоящая из двух лучей с общим началом и ограниченной ими части плоскости, называется углом.

За единицу измерения углов принимают угол в 1 градус – часть развёрнутого угла. Существует ещё одна единица измерения величины угла – 1 радиан.

Обобщенным углом (углом поворота) называется плоская фигура, образованная лучами, выходящими из одной точки, называемой вершиной угла, причем указано, какой из этих лучей считается первым (начальной стороной угла) и как его вращать до совпадения со вторым (конечной стороной угла).

При таком определении угла его величина рассматривается как мера поворота конечной стороны относительно начальной.

Положительным направлением вращения считается вращение против часовой стрелки, а отрицательным – по движению часовой стрелки.

Определение: Угол в 1 радиан есть центральный угол, опирающийся на такую дугу окружности, длина которой равна радиусу этой окружности.

Определение: Единичная окружность (тригонометрический круг) – окружность с центром в начале координат, радиус которой равен единице.

Длина окружности содержит 2 радиуса, следовательно,

360 = 2 (рад),

180 =  (рад).

1 радиан = 1 = радиана

Полезно пользоваться таблицей часто встречающихся величин углов в градусах в радианы и обратно.

А°	0°	30°	45°	60°	90°	180°	270°	360°
α	0							2

Начальное положение луча совпадает с направлением у оси ох.

Положение точки А на единичной окружности соответствует и величине угла (дуги). В 0°, и 360°, 720° и т.д. т.е. 0, 2, 4, 6 и т.д. радиан.