Диадное произведение векторов (базиса)

Скалярное произведение двух базисных векторов называется диадой:

e_ie_j,

Свойства диад:

1. e_ie_j= e_je_i

2. e_i(ae_j + be_k)=ae_ie_j + be_ie_k,

a,b - числа

3. Каждой диаде ставится в соответствие матрица 3*3, состоящая из нулей и одной единицы:

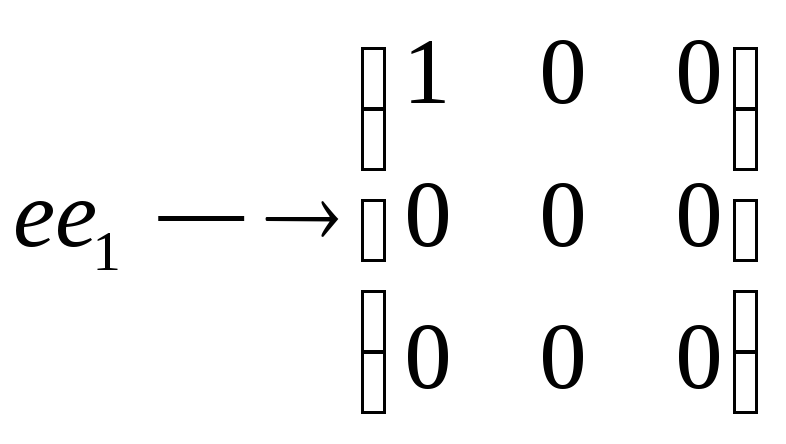
Лекция №3

1. Определение пространства Евклида

2. Норма(длина) вектора. Ортонормированный базис.

3. 1. Определение пространства Евклида

Определение: вещественное пространство называется евклидовым, если каждой паре векторов ,изпоставлено в соответствие вещественное число (,), называемоескалярным произведением, причём выполнены следующие аксиомы:

1. –переместительный закон

2. –сочетательный закон

3. –распределительный закон

4. , при ,, ,

для произвольных векторов ,,изи произвольного вещественного числа.

Зачастую в физике, механике и других дисциплинах приходится иметь дело с физическими величинами имеющими направление: сила, скорость и т.д. Их взаимодействие приводит к появлению понятия скалярного произведения векторов.

Скалярное произведение ненулевых векторов ,записывается следующим образом:

(3.1)

Если два вектора заданы базисом, то их скалярным произведением является сумма попарных произведений в соответствующих координатах:

Например возьмём декартову систему координат, которая является системой координат, евклидова пространства. В этой системе выберем векторы x и y, записанные в ортах :

Норма вектора. Ортонормированный базис

Согласно аксиоме (4) скалярный квадрат любого вектора есть неотрицательное вещественное число .

Определение: Неотрицательное значение квадратного корня из этого числа называется длиной (нормой) вектора x и обозначается , т.е.

Свойства: отсюда видно , что

1. нулевой вектор является единственным вектором, длина которого равна нулю.

2. при умножении вектора на число, длина вектора умножается на модуль этого числа.

3. вектор длина которого равна единице называется нормированным,

Любой ненулевой вектор y можно нормировать, умножив его на некоторое число:

–нормирующий множитель.

Система векторов является нормированной, если нормированы все её векторы.

Одним из основных понятий также является понятие ортогональности.

Определение: Считается, что векторы ,ортогональны, еслиобозначение.

В декартовой системе координат это характеризуется перпендикулярностью векторов.

Теорема1: Всякая ортогональная система ненулевых векторов является линейно независимой.

Доказательство: Пусть существует ортогональная система ненулевых векторов , выполняется равенство:

(3.7)

умножим обе части скалярно на какой-нибудь вектор :

,

Так как векторы e₁ ортогональны, то все скалярные произведения кроме равны нулю. Получено:

,

так как .

А это доказывает линейную независимость ортогональных векторов.

Если базис евклидова пространства представляет собой ортогональную систему векторов, то этот базис называют ортогональным.

В линейном пространстве все базисы равноправны. А в евклидовом пространстве скалярное умножение позволяет выделить среди всех базисов ортогональные и ортонормированные, которые играют роль, аналогичную роли прямоугольной системы координат в аналитической геометрии.

Определение: Ортогональный базис называют ортонормированным, если каждый вектор этого вектора имеет норму, равную единице.

Любой ортогональный базис легко преобразовать в ортонормированный, умножая векторы на соответствующие нормирующие коэффициенты. (разделив каждый вектор базиса на его длину).

Из любого произвольного базиса можно создать ортонормированный базис. Этот способ преобразования называется процессом ортогонализации Грама-Шмидта. Алгоритм заключается в следующем.

Пусть f=(f₁,…,f_n) – некоторый базис n – мерного евклидова пространства . Преобразовывая этот базис, построим ортонормированный базис. Для этого последовательно вычислим векторыи так далее. По формулам:

,

,

,

.

Процесс ортогонализации изображён на рисунке 1.

Для обоснования алгоритма необходимо чтобы векторы не были нулевыми и были попарно ортогональными.

Докажем это. Предположим, что некоторый вектор g_k+1=0, тогда:

, (3.11)

то есть (3.12)

то есть вектор является линейной комбинацией векторов, которые в свою очередь выражаются через векторыв силу 3.10. Это говорит о том что система векторов– линейно зависима. То есть утверждениепривело к противоречию и поэтому его можно считать неверным.

Для определения ортогональности, векторов скалярно умножим (3.11) на вектор , где.

(3.13)

Поскольку скалярное произведение равно нулю, то вектор ортогонален вектору .

Таким образом, в конечномерном (определённой размерности) евклидовом пространстве существует ортонормированный базис.

Лекция №4

Алгебра линейных операторов

1. Алгебра линейных операторов.

2. Числовые характеристики линейных операторов и его матрицы.

3. Собственны числа, векторы.

4. Характеристический многочлен.

Действия над линейными операторами

Основными алгебраическими действиями на линейными операторами являются следующие:

А) умножение линейных операторов

Б) умножение линейного оператора на число

В) сумма линейных операторов

Рассмотрим подробнее каждую из операций.

А) Пусть в линейном пространстве заданны два линейных преобразованияи. Применяя к произвольному векторуизсначала преобразование, а затем, получим некоторый вектор

. (1)

Определение: преобразование переводящие вназывается произведениемна.

(2)

матрица преобразования линейных операторов иравна произведению матриц этих операторов:

(3)

Правило: обратное преобразование имеет обратную матрицу. Чтобы линейное преобразование было обратным необходимо и достаточно, чтобы была обратной и его матрица.

Б) Умножение линейного оператора на число.

Определение: Преобразование, полученное в результате применения к некоторому вектору сначала преобразования, а затем умножения нового вектора на число, называется произведениемнаи обозначается:

(4)

Матрица произведения числа на линейный оператор равна произведению этого числа на матрицу этого линейного оператора.

Свойствам произведений линейных операторов:

1. 

2. 

3. 

4. 

В) Сумма линейных операторов

Возьмём какие либо два преобразования илинейного пространстваи каждому векторуизпоставим в соответствие вектор. Преобразование переводящиев, обозначаетсяи называется суммойи.

(5)

Матрица сумм преобразований равна сумме их матриц.

Свойства суммы линейных операторов:

1. 

2. 

3. 

4. 

5. 

6.