Discussion

1. Compare all the characteristics of a conventional mode-locked laser with those of the reported one. What are the advantages of the latter?

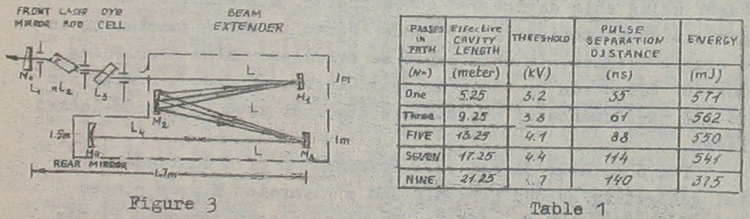
2. Study carefully the diagram of the compact design in Fig.3. Is it different from the design of a conventio-nal solid state mode-locked laser? What are the differences?

3. Applications mау include dynamic remote sensing and ranging of objects to mention a few. Do you know any other applications? Could they bе possible in case of a typical mode-locked laser?

Terminology B:

1. intensity - dependent light transmission – управляемое светоиспускание;

2. walk-off effect – эффект блуждания;

3. do-uble - pass generation – двупроходимая генерация.

Vocabulary Practice

1. Find the equivalents of the word-combinations in Text 12B:

разделение амплитуд, произвольное отношение, быстрое реагирова-ние, идеальное фазовое соответствие, эффективность мгновенных преобразований, более отчетливо выражать, грубые (приближенные) оценки, круговые пробежки, за пределами темы данной статьи, заслуживает упоминания, технология пассивной синхронизации мод.

2. Translate the sentences to obtain the abstract of Text 12B:

Прибор, состоящий из нелинейного кристалла и дихроичного (глу-хого) зеркала, обладает особенностью управляемого отражения и может использоваться как пассивный синхронизатор мод. Было рас-считано укорачивание импульса для нормализованного Гауссова импульса, обусловленное отражением с помощью нелинейного зер-кала. Сделано сравнение с показателями насыщающегося поглоти-теля, используемого для синхронизации мод.

TEXT 12В PULSE SHORTENING BY A NON-LINEAR MIRROR MODE LOCKER

Saturable absorbers exhibit intensity-dependent light transmission. In mode-locked lasers this feature is used to perform amplitude discrimination and pulse shortening. Pulse shortening has been analyzed in the case of a fast absorber, in the inter-mediate case, and has been calculated for an arbitrary ratio of the pulse duration to the absorber relaxation time.

Recently a novel nonlinear optical device utilizing second harmonic generation was proposed. It may exhibit intensity-de-pendent reflection or transmission with a fast time response in the subpicosecond range. Successful mode locking of a Nd:YAG laser using this device was demonstrated. Since one of the im-portant characteristics of a mode locker is pulse shortening in a single transit, in this paper we calculate pulse shortening due to reflection by the nonlinear mirror and make a comparison to the performance of a saturable absorber used in a mode-locked laser.

The nonlinear mirror is a combination of a nonlinear crys-tal generating second harmonic and a dichroic mirror placed behind it. The incident light generates second harmonic in the crystal and the dichroic mirror reflects totally the second harmonic and partially the fundamental radiation back into the nonlinear medium. Same means are provided to adjust the phase differences φ = 2 φ1 - φ2 (φ1, φ2 are the phases of the fundamental and second harmonic waves) to be -π/2 + 2mπ. After reflection by the dichroic mirror in the second pass through the crystal a reconversion of the second harmonic into fundamental takes place. The reflection of this device in these conditions increases by increasing the light intensity.

If the phase difference φ = π/2 + 2mπ, in the second pass further conversion into second harmonic is provided. Then, the action of the device is equivalent to a double-pass second harmonic generation with some modification of the wave intensi-ties after the first pass. In this case the reflected intensity decreases by increasing the input one.

The analysis shows that both higher conversion efficiency and lower reflectivity of the dichroic mirror at the fundamental wavelength enhance the nonlinearity in light reflection. An ex-pression for the nonlinear reflection coefficient at the funda-mental wavelength Rnl as a function of the conversion efficiency ŋ and the dichroic mirror reflectivities at the fundamental, RI, and the second harmonic, R2, has been derived for the case of in-terest, i.e., when. φ = -π/2 + 2mπ. If the dichroic mirror is totally reflecting at the second harmonic, the nonlinear reflec-tion is given by

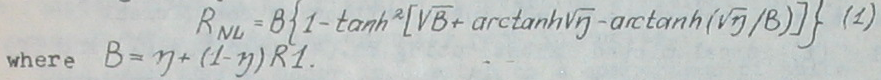
The reflection coefficient RI may be regarded as a small-sig-nal reflection analogous to the small-signal transmission of a saturable absorber, if we consider a light pulse reflected by the nonlinear mirror, the high-intensity parts of the pulse will be more efficiently reflected than the low-intensity parts. Hence, one expects pulse shortening, similar to that experienced by a light pulse passing through a saturable absorber. In accor-dance with the above brief discussion on the effect of the phase difference it is evident that the pulse shortening maximizes for φ = -π/2 + 2mπ. Deviation from this will reduce the pulse shortening and approaching φ = π/2 + 2mπ pulse broade-ning will result.

In what follows, we calculate the pulse shortening of a nor-malized Gaussian pulse with FWHM = 1 for ξ = -π/2 + 2mπ (2). A phase difference change within +/- (п/6) reduces the modelocking probability to ≈50%.

We confine our treatment to plane waves and perfect phase matching. The walk-off effect is compensated, since after reflec-tion by the dichroic mirror the fundamental and second harmonic beams travel exactly the same optical paths. Thus, the only influence of the walk-off effect is reduction of the conversion efficiency. In addition, we assume pulse duration for which the crystal length is smaller than

are the group velocities for the fundamental and the second harmonic. This assures that the group velocity mismatch does not broaden the second harmonic pulse. For reasonably high conversion efficiencies the pulse durations in these conditions are in the 0.2-5-ps range, depending on the type of crystal and the wave-length region. Higher-order effects like dispersion spreading are neglected.

First we analyze the pulse shortening as a function, of the peak conversion efficiency. Thus, the incident Gaussian pulse with FWHM = 1 has the form

.

We use the following рrocеdure; the instantaneous conversion efficiency ŋ (t) is determined using the relation

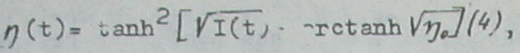
where ŋ is the peak conversion efficiency at t = 0 for a pulse of unity peak intensity. Next, the instantaneous nonlinear reflection coefficient R (t) is calculated, substituting Eq. (4) into Eqs. (I) and (2). The reflected pulse form I_r(t) (at the exit of the nonlinear mirror, i.e., at the left-hand side of the crystal NLС) is given bу I_r(t) = I(t)Rnl(t) (5).

Lastly, we calculate the time at which the reflected intensity drops to half of its maximum value. The full wilth at half-maximum of the reflected pulse is a function of the peak conversion efficiency of the incident pulse for various va-lues of the dichroic mirror reflectivity HI at the fundamental wavelength. As one can expect, the pulse shortening is more pro-nounced for high conversion efficiency. However, it peaks conversion efficiency in the range of 0.6-0.8 and then rapidly approaches the incident pulse duration. This is to be expected, since for a very high conversion the second harmonic pulse fol-lows closely the pulse form of the fundamental (of course not in the wings) due to saturation.

By inspection of the expression for the reflected pulse form Eq. (5) it can be seen that the pulse shape is modified by the nonlinear reflection coefficient, which is a rather complex function. Thus, the reflected pulse shape does not follow the input one.

It is also evident that the pulse shortening is higher for lower reflection coefficient RI. This is in accordance with the features of the nonlinear mirror mentioned above. Here we remind the reader that the pulse shortening and the amplitude discrimination starts at conversion efficiency of the order of several percent as the mode-locking experiment has revealed. A reasonable question is why is the pulse shortening not close to аs one can expect for low conversion efficiency. It is well known that for a Gaussian pulse after the first pass through the nonlinear crystal the second harmonic pulse is shortened with respect to the fundamental by this factor. The reason is that the fundamental pulse will broaden because of the high in-tensity parts. In the second pass through the crystal the broadened fundamental pulse is amplified in the field of the second harmonic pulse, thus the effect of the pulse shortening in the second harmonic generation is somewhat reduced.

Finally, we illustrate pulse shortening as a function of the incident peak pulse intensity. Conversion efficiency of 0.5 is assumed for a pulse having unity peak intensity.

This part of the paper is devoted to a comparison of pulse shortening by the nonlinear mirror to that оf a saturable absorber when used аs a mode looker. The advantages of the nonlinear mirror such as simplicity, reliability, wide spectral ranges of operation, simultaneous generation of ultrashort light pulses at the second harmonic, and fast time response have been discussed. Because of the fast time response one might expect better per-formance of the nonlinear mirror in comparison with alow absor-bers, at least for solid-state lasers. Therefore we compare pulse shortening to that of a fast absorber. When a single-pass extracavity pulse shortening is required, saturable absorbers of very low small-signal transmission of the order of 10^-7 are superior and may provide an optimized pulse reduction by a factor of 3. However, in mode-locked solid-state lasers, the small-signal transmission ranges from 0.5 to 0.8. The optical arrangement with an absorber corresponding to the nonlinear mirror is a dye cell with a totally reflecting mirror behind it. Since the light passes twice through the cell, the low intensity trans-mission is 0.25-0.64. Thus, the corresponding relative pulse shortening [defined as (T - T_p )/T_p] may reach values in the range from -0.16 to -0.06. Here we note that these are the maximum values attainable at an optimized intensity level only.

Considering a nonlinear mirror, intracavity conversion effi-ciencies of 0.5 can be realized with highly efficient nonlinear crystals such as KTP and BBO. Fоr RI ≈ 0.25-0.64 (small-signal reflection) the relative pulse shortening is in the range from -0.11 to -0.05, i.e., somewhat smaller but very close to that of the absorber. However, in a mode-locked laser the absorber pulse shortening maximizes at a certain intensity level, while the non-linear mirror one increases monotonically for all realistic va-lues of intensities and conversion efficiencies.

To reveal the ultimate capabilities of the nonlinear mirror with respect to pulse shortening one has to perform an analysis assuming nonstationary second harmonic generation and reconversion. However, some crude estimates are possible. For the experiment where 5.5-mm long KTP crystal was used, effective pulse shor-tening may be expected for pulses as short as 4 ps. especially favorable is the situation for mode locking an Nd: glass laser using a KDP crystal. In this case for a 2-cm long crystal pulses as short as 200 fs may still undergo pulse shortening. In both examples one can expect generation of ultrashort pulses with a duration determined by the spectral gain profile (if there are no other limitations, such as self-phase modulation or limited number of round trips). A comprehensive analysis of laser dynamics, including the effect of the nonlinear mirror and laser active medium, is out of the scope of this paper.

It is worth mentioning that the change of phase difference does not limit the bandwidth of the device, but only changes the direction of the interaction between the lightwaves in the second pass, i.e., reconversion back into fundamental or further conversion into second harmonic. Also, since the group velocity dispersion in air is several orders of magnitude less than in nonlinear crystals, the crystal mirror separation does not im-pose any practical limitations on the performance of the nonli-near mirror mode locker with respect to the bandwidth.

10700 п. зн.

Rewiew

1. Read text 12В attentively. Divide it into logi-cal sections (see Text 12A).

2. Think of a good title for each section.

3. Mark phrases which best serve as the main idea of each section. Give reasoning for your choice.

4. Combine the topic sentences and write a summary of the text.

5. Speak on the problems presented in Text 12B:

1. Analysis of pulse shortening due to reflections by a non-linear mirror.

2. Comparison of the performance of the nonlinear to that of a saturable absorber mode locker.

3. Advantages of the new mode-locking device.

6. Look through Text 12C and answer these questions:

1) What does the mode selection depend on? 2) What type of the modes is the most preferable to work with and why? 3) Why is it necessary to make laser oscillate in the lowest order mode? 4) What influences the laser output directionality? 5) How does the volume of the active material depend on the cavity length?

TEXT 12 С TRANSVERSE AND LONGITUDINAL MODE SELECTION

Since optical resonators have dimensions which are large in comparison to the wavelength of light, there will, in gene-ral, be a large number of modes which fall within the atomic linewidth and which can oscillate in a laser. Thus the output say consist of a number of longitudinal modes each oscillating at a different frequency. Also, since the various transverse modes have different phase and amplitude distributions across the output plane, the resulting laser output may not be highly direc-tional. In fact the power per frequency and solid angle inter-val is maximum when the laser oscillates in - single mode which is the fundamental mode. In order to obtain highly directional and spectrally pure laser output, various techniques have been developed both for transverse and longitudinal mode selection in lasers. In this section we will briefly discuss some of the important mode selection techniques.

Transverse Mode Selection

As we showed above, the lowest-order transverse mode has a Gaussian amplitude distribution across a transverse plane. It is this mode that one usually prefers to work with as it has no abrupt phase changes across the wave front(as the higher-order transverse modes have) and has a monotonically de-creasing amplitude away from the axis. This leads to the fact that it can be focused to regions of the order of the wavelength of light, producing enormous intensities. The Gaussian mode has the narrowest distribution and hence if an aperture is introduced in the cavity which increases the loss of the next higher order transverse mode to a value where the loss exceeds the gain, the laser would oscillate only in the lowest-order mode. Observe that this introduces additional losses even for the lowest-order mode. Specific higher-order transverse modes can also be selected at a time by choosing complex apertures which introduce high loss for all modes except the required modes or by profiling the reflectivity of one of the mirrors to suit the required mode. Thus, a wire placed normal to the axis and passing through the resonator axis would select the second-order TE_OI mode.

Longitudinal Mode Selection

Even when a laser is oscillating in a single transverse mode, it could be oscillating in different longitudinal modes separated by a frequency spacing of c/2d. One possible method to obtain single-mode oscillation is to decrease the length of the cavity d to such a value that there is only one longitudinal mode within the gain profile which has its gain higher than the losses. Such a method can be used with gas lasers which have relatively small linewidths. It must be noted that as the length of the laser cavity is decreased, the volume of the active material also decreases and hence the output power would also decrease.

In solid state lasers the bandwidth is large and the above technique becomes, impractical. Hence various other techniques have been envolved for longitudinal mode selection.

3000 п. зн.

7. Translate the text below in writing using a dictionary:

TEXT 12D HYBRID SYSTEMS

Hybrid techniques generate shorter pulses than the corres-ponding synchronously pumped systems. The hybrid systems incor-porate a saturable absorber folded section in the standard syn-chronously pumped cavity arrangement. Critical submicrometer cavity matching is still required to achieve minimum output poi-se durations. All the active-passive dye combinations can be used in the hybrid arrangement, with the exception of the Coumarin 6 active dye that cannot be effectively excited by 532-, 511—, or 355-nm radiation. The choice of the saturable absorber in the hybrid technique is less critical than in the purely pas-sive system; therefore, the available wavelength range is broa-der.

One further advantage of the synchronous-pumping method is that the dyes with very short lifetimes, which would preclude true CW operation, can be made to lase. Synchronously pumped la-sers with subpicosecond pulses have been operated up to a wave-length of 1.35μm, and hybrid systems have produced less than 3OO-fs pulses around 97O nm.

The passively mode-locked laser represents the simpliest system in that a mode-locked pump source is not required.

1100 п. зн.

SUPPLEMENTARY READING TASKS

CHOOSING А NONLINEAR CRYSTAL

The key factors for material selection depend not only upon the laser conditions – beam size, beam quality and beam power density – but also upon the crystal's properties, such as phase matching, transparency, damage threshold and temperature stability.

Tunable laser sources ranging from the ultraviolet to the infrared may be achieved by frequency conversion of fixed-wave-length or tunable lasers by using nonlinear crystals. Second harmonic generation (SHG), third harmonic generation (THG) and sum frequency mixing (SFM) have been widely used for frequency up conversion (i.e. the shifting of an optical beam to shorter wavelengths). Optical parametric oscillation (CPO), on the other hand, provides a means for frequency down-conversion with conti-nuously angle or temperature-turned output. Shorter-wavelength (100 to 200 nm) and middle-infrared coherent sources may also be obtained by further Raman-shifting of the nonlinear- crystal-converted output.

Using the direct output of commercial lasers or their har-monics as the pumping sources, ОPО in nonlinear crystals provides a very wide tuning spectrum, from the far infrared to the vacuum ultraviolet.

Materials Selection Rule

The key issues of materials selection for frequency conver-sion may be summarized as follows:

• high conversion efficiency;

• high damage threshold,

• wide phase-match and transparency range;

• large size with good optical homogeneity;

• low cost and easy fabrication;

• chemically (free of moisture) and mechanically stable.

FEATURES OF THE BBO CRYSTAL

The salient features of the BBO crystal may be readily summa-rized. First, it has a very wide transparency and phase-matching, angle-tuning range: 190 to 300 nm. Second, it has a high damage threshold – up to 13 GW/cmІ at 1.06 m and a 1-ns pulsewidth –and a wide temperature acceptance width of 55°C. This tempera-ture acceptance width is about ten times as large as that of KDP and twice that of KTP. Third, BBO has a very high non-linear coefficient. BBO's d₂₂ value is 4.1 x that of KDP's comparable d₃₆-value, which makes BBO's effective figure of merit 3 to 14 times better that that of KDP for second harmonic generation at 1064 nm.

Fourth, BBO is chemically stable and nearly free of moisture. Fifth, good-quality BBO cry-stals are commercially available at reasonable prices in sizes as large as l0 x 10 x 10 mm. BBO crystal has been identified as a prime candidate for fre-quency doubling dye lasers to generate deep-ultraviolet sources. Efficient (relatively speaking, of course), tunable sources in the 201 – to 310-nm range have been reported for phase-matching at room temperature. More recently, а 195-nm source has been achieved using BBO at low temperature for sum frequency mixing the outputs of dye lasers. Commercial dye laser systems with excimer lasers as pumps, using BBO crystals for internal fre-quency-doubling, are also available. A vacuum-ultraviolet source at 71 nm was recently reported; it involved third harmonic generation, in neon gas, of the BBO-generated 213-nm fifth harmonic of a Nd:YAG laser. Peak output powers of I to 2 W from this fifteenth-harmonic generator have been measured.

Nonlinear crystals play an essential role for the genera-tion of coherent sources in spectral regimes where useful levels of direct output from existing lasers cannot be achieved. An ideal crystal should include all the features of transparency and phase-matching over a wide spectral range; wide angular, tempe-rature and spectral acceptance widths; high damage threshold, high nonlinear coefficient; high degree of homogeneity over relatively large volumes; and chemical and mechanical stability. Finally, crystal cost, in terms of efficiency per dollar, should be reasonable. For high-average-power laser applications, such as laser fusion, developmental goals for such crystals as KDP, LAP and BBO will center on high damage thresholds and large crystal sizes, with diameters up to 20to 40cm.

For low-power laser applications such as diode-pumped la-sers and integrated-optics devices, crystals with extremely high nonlinear coefficients (100 to 1,000 times that of KDP) and/or very long aperture length will be required. Along this line, improvements in crystal-growth technology have been emphasized. They include the growth of film and fiber crystals, fabrication of guided-wave devices, growth of new organic crystals and growth of quasi-phase-matching crystals.

CW-PUMPED DYES YIELD ULTRASHORT LASER PULSES

Since its introduction in 1972, the passively mode-locked CW-pumped dye laser has been the source of the shortest pulses with 27 fs being the minimum pulse directly generated from such a system. This 27-fs laser employed the original ac-tive/passive dye combination of Rhodamine 6G and 3, 3 , Diethy-loxadicarbocyanine iodide(DODCI). Until 1986, this was the on-ly widely reported passively mode-locked CW-pumped dye-laser scheme and operated in the red region of the spectrum around 620 nm. Since then, many mоrе active/passive dye combinations have been identified, and continuous tunability of femtosecond pul-ses is now possible throughout most of the visible spectrum.

Absorption and amplification

The mechanism for short-pulse generation in a passively mo-de-locked dye-laser system relies on the action of saturable ab-sorption and saturable amplification. The saturable absorption attenuates the front or leading edge of the pulse. On encounte-ring the gain medium, the center of the pulse experiences ampli-fication and depletes the available gain such that the rear or trailing edge of the pulse sees no gain and is preferentially suppressed. The ability to generate stable mode-locked pulses is defined by a parameter S, which is given by Rσa/σg, where σg and σa are the dye gain and absorber cross sections, respectively, and R is the ratio of the beam areas in the gain and absorber media.

Reliable mode-locking requires S> 2. In physical terms, this means that the absorption saturates more easily than the gain. As an aid to achieving this condition, the beam area in the gain medium can be larger than that in the absorber through the choi-ce of radius of curvature of the appropriate cavity-folding mir-rors.

Argon-ion-laser source

For all the active dyes shown, a CW argon-ion laser can be used as the excitation source. Using Coumarin 6H and Coumarin 102, all-lines UV pumping is required. Improved operation and enchanced output from tnese passively mode-locked systems have been achieved with the introduction of high-UV average-power (up to 5 W) argon-ion-laser systems. In the lasing range 550-700 nm the all-lines visible output from a small-frame argon-ion laser producing up to 5 W average pump power is adequate to achieve pas-sively mode-locked operation. Rhodamine 700 and Rhodamine 800 possess principal absorption bands in the region of 650-700 nm; therefore, krypton-ion pumping is preferable.

SUPPLEMENTARY READING TASKS