Вопрос 11 12 Чистая Нижняя и верхняя цена игры.

Пусть 1 игрок имеет m стратегий ,2 игрок n стратегий.

Матрица выигрыша 1 игрока

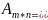
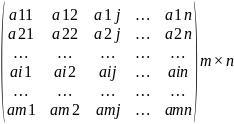
min 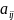(I = )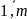

j

max min =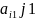 =α(*)

I j

Определение: Чистой нижней ценой игры наз-ся число α,определенное по формуле(*)

Max (j=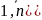

I

max min =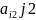 =β(**)

I j

Определение: Чистой верхней ценой игры наз- ся числа β,определенные по формуле (**)

Вопрос 13.Седловая точка

Седловой точкой игры называют точку, в кот α=β. Решением матричной игры наз.седловая точка или седловой элемент.

Седловой точкой (хₒ;уₒ) для функции f(х,у) называется точка, удовлетворяющая неравенству:

F(x,yₒ)≤f(xₒ,yₒ)≤f(xₒ,y)

для любого х, у. (хєА;yєB)

Вопрос 14. Оптимальные чистые стратегии.

На промышленных предприятиях теория игр может применяться для выбора оптимальных решений, например при создании рациональных запасов трудовых ресурсов, сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличения запасов, гарантирующих бесперебойную работу про-ва, и сокращения запасов в целях минимизации затрат на их хранение. В с/х теория игр может применяться при решении таких экономических задач, как выбор посева одной из возможных культур, урожай которой зависит от погоды, если известна цена единицы той или иной культуры и средняя урожайность каждой культуры в зависимости от погоды. В этом случае одним из игроков является с/х предприятие, стремящееся обеспечить наибольший доход, а другим - природа.

Решение подобных задач требует полной определенности в формулировании их условий( правил игры): установлении кол-ва игроков, выявления возможных стратегий игроков и возможных выигрышей.

Важным элементом в условии игровых задач является стратегия – совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор действий данного игрока. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а её элементы – чистыми стратегиями. Количество стратегий у каждого игрока может быть конечным и бесконечным, в зависимости от этого игры подразделяются на конечные и бесконечные.

Понятия оптимальной стратегии , цены игры, среднего выигрыша находят отражение в определении решения игры: стратегии P* и Q* первого и второго игроков соответственно называются их оптимальными стратегиями, а число V – ценой игры, если для любых стратегий P первого игрока и любых стратегий Q второго игрока выполняются неравенства:

M(P,Q*)≤V≤M(P*,Q) ,где M(P,Q) означает математическое ожидание выигрыша первого игрока, если первым и вторым игроками избраны соотв. Стратегии P и Q.

Из данного неравенства следует, что V=M(P*,Q), т.е. цены игры равна математическому ожиданию выигрыша первого игрока, если оба игрока изберут для себя оптимальные стратегии.

Вопрос 15.Смешанные стратегии

Смешанными стратегиями игрока наз. перечень вероятностей, с кот. игрок применит свои чистые стратегии.

Пусть 1й игрок имеет m чистых стратегий: 1,2,3,…,m

х-смешан.стратегия 1го игрока

х=(х_1,х_2,..., х_m)

х_i ≥0 ∑ х₁ =1 i=1,m

Пусть 2й игрок имеет n чистых стратегий: 1,2,3,..,n

у- смешан.стратегия 2го игрока

у=(у_1, у_2,…, y_n)

y≥0 ∑y_j=1 j=1,n