
- •Вопрос 1 Целевая функция.Критерием( или целевой функцией) называют функцию, переменными которой явл.
- •Вопрос 2 Градиент функции.
- •Вопрос 3. Общая задача линейного программирования
- •Вопрос 4. Стандартная задача л.П.
- •Вопрос 5. Каноническая форма записи задачи л.П.
- •Вопрос 6. Симметричные и несимметричные двойственные задачи( теория двойственности)
- •Вопрос 8. Метод северо-западного угла
- •Вопрос 9. Метод потенциалов
- •Вопрос 11 12 Чистая Нижняя и верхняя цена игры.
- •Вопрос 13.Седловая точка
- •Вопрос 14. Оптимальные чистые стратегии.
- •Вопрос 15.Смешанные стратегии
- •17. Точка безубыточности (тбу)
- •Вопрос 18. Примеры эконометрич. Моделей (производственная функция)
- •Вопрос 19.Функциональные, стохастические связи.
Вопрос 1 Целевая функция.Критерием( или целевой функцией) называют функцию, переменными которой явл.
В экон. задаче критерий (обычно) задает един. способ управления моделью. Например, критерием может быть общий объем производства прибыль( исслед на max) либо затраты ( исслед на min) (Целевую функцию можно записать в виде суммарной стоимости произведенной продукции)

Или

Вопрос 2 Градиент функции.
Градиентом
функции функции Z=f( )
наз-ся вектор (напр. отрезок) с координатами
)
наз-ся вектор (напр. отрезок) с координатами
( ,
,
 )
обозн.
grad f
)
обозн.
grad f
Пример
f
( = 2
= 2 +5
+5
=
(2 )’
= 2
)’
= 2
=
( = 5
= 5


 5
5
gead f (2,5)

(0,0) 2
Вопрос 3. Общая задача линейного программирования
Функция n переменных x1, x2, ... xn
![]() .называется линейной
функцией,
если она представима в виде линейной
комбинации переменных, то есть в виде
суммы переменных с постоянными
коэффициентами
.называется линейной
функцией,
если она представима в виде линейной
комбинации переменных, то есть в виде
суммы переменных с постоянными
коэффициентами
![]() . Задачей
линейного программирования называется
задача, состоящая в нахождении
экстремального (максимального или
минимального) значения линейной
функции
. Задачей
линейного программирования называется
задача, состоящая в нахождении
экстремального (максимального или
минимального) значения линейной
функции![]() при
условии, что переменные удовлетворяют
системе линейных равенств и неравенств:
при
условии, что переменные удовлетворяют
системе линейных равенств и неравенств:
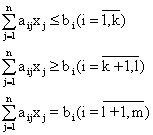 Функция,
экстремальное значение которой требуется
отыскать, называется целевой
функцией.
Система равенств и неравенств называется
системой
ограничений.
Функция,
экстремальное значение которой требуется
отыскать, называется целевой
функцией.
Система равенств и неравенств называется
системой
ограничений.
Всякий набор значений переменных, то есть вектор X значений,
![]() называется планом задачи.
План называется допустимым планом,
если он удовлетворяет системе ограничений.
Обычно (но не всегда) множество допустимых
планов бесконечно. На разных планах
целевая функция принимает различные
значения. Задача линейного программирования
требует, чтобы среди всех допустимых
планов был найден тот план, на котором
целевая функция достигает искомого
экстремального значения (максимального
и минимального, в зависимости от
конкретной задачи). Такой план
называется оптимальным
планом.
Значение целевой функции на оптимальном
плане называется оптимумом.
называется планом задачи.
План называется допустимым планом,
если он удовлетворяет системе ограничений.
Обычно (но не всегда) множество допустимых
планов бесконечно. На разных планах
целевая функция принимает различные
значения. Задача линейного программирования
требует, чтобы среди всех допустимых
планов был найден тот план, на котором
целевая функция достигает искомого
экстремального значения (максимального
и минимального, в зависимости от
конкретной задачи). Такой план
называется оптимальным
планом.
Значение целевой функции на оптимальном
плане называется оптимумом.
Решить задачу линейного программирования - значит найти ее оптимальный план и оптимум.
Вопрос 4. Стандартная задача л.П.
f (
( )
=
)
=
 =
=
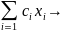 max
max
 ≤
≤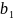

…………………………………

 ,
,

Матрица А – матрица коэффициентов

f(
x=
 - вектор столбец b=
- вектор столбец b= - вектор столбец
- вектор столбец
Короткая запись стандартной задачи Л.П.
(c,x)
 max
max
x=( ),
c=(
),
c=(

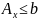
x x,
b
– векторы столбцы
x,
b
– векторы столбцы
Замечание
U где
u
=
где
u
= , v
=
, v
=
 =>
=>
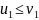

…………

Вопрос 5. Каноническая форма записи задачи л.П.
Все нер-ва в ОДР станут равенствами
f(

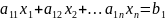

………………………………….

,
Короткая запись канонич. задачи Л.П
(c,x)
x=
 )
, c
= (
)
, c
= (


 x,
b
– векторы столбцы
x,
b
– векторы столбцы
Замечание. Любую задачу линейного программирования можно привести к канонической форме записи.
