- •Содержание
- •Расчет посадки для гладкого цилиндрического соединения с натягом.
- •Расчет переходной посадки.
- •Расчет посадки подшипника качения
- •Расчет калибров деталей гладкого цилиндрического соединения.
- •Расчет резьбового соединения.
- •Расчет калибров для резьбового соединения м56–7h/8g.
- •Литература

Аносов А.Ю. – Челябинск: ЮУрГУ,АК-304, 2012, 20 с., 8 ил.,библиогр. список: 4наим.
В настоящей работе соответствии с вариантом семестрового задания рассчитываются посадки для сопрягаемых элементов сборочного узла: посадка с натягом; вероятность образования зазора в переходной посадке; посадки подшипников качения. Также производится расчет калибра-скобы и калибра-пробки, расчет резьбового соединения и калибров резьбового соединения.
К работе прилагаются чертежи деталей: поз. 4 вал и 12 зубчатое колесо, а также чертежи калибра-скобы и калибра пробки, для контроля размеров сопрягаемых деталей 4 и 10.
Содержание
Y
Содержание 3
Расчет посадки для гладкого цилиндрического соединения с натягом. 4
Расчет переходной посадки. 7
Расчет посадки подшипника качения 10
Расчет калибров деталей гладкого цилиндрического соединения. 12
Расчет резьбового соединения. 14
Расчет калибров для резьбового соединения М56–7H/8g. 16
Литература 20
Расчет посадки для гладкого цилиндрического соединения с натягом.
Согласно варианту задания, для сопряжения деталей 4-12 имеем следующие данные: D=65, dн=65, d2=160, l=65, Mкр=180 Нм, f=0,15. Остальные данные приведены ниже в таблице 1.1.
деталь 12 |
деталь 4 |
материал: сталь 40Х |
материал: сталь 45 |
σт=80∙107 Н/м2 |
σт=80∙107 Н/м2 |
µ=0,3 |
µ=0,3 |
E=2∙1011 Н/м2 |
E=2∙1011 Н/м2 |
Таблица 1.1
Минимальный натяг определяется из условия прочности соединения
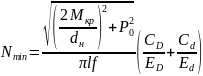 ,
(1.1)
,
(1.1)
где CD и Cd – коэффициенты жесткости конструкции.

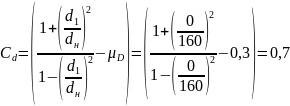
Подставляя найденные значения CD и Cd в формулу (1.1), получаем Nmin=2,165 мкм. Максимальный натяг определяется из условия обеспечения прочности деталей.
 ,
(1.2)
,
(1.2)
где для вала и отверстия, соответственно имеем:
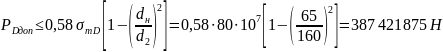 ,
,
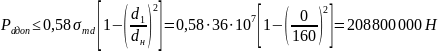 .
.
Nmax рассчитывается
по наименьшему
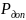 :
:
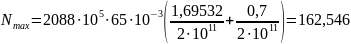 мкм.
мкм.
Находим функциональный допуск посадки:
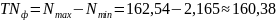 мкм.
мкм.
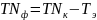
Конструкторский
допуск посадки
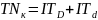 .
Эксплуатационный запас
.
Эксплуатационный запас
 ,
где
,
где
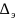 – запас на эксплуатацию и
– запас на эксплуатацию и
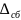 – запас на сборку соответственно. Для
посадок с натягом
– запас на сборку соответственно. Для
посадок с натягом
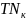 должен
быть не точнее
должен
быть не точнее
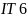 и не грубее
и не грубее
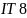 ;
;
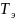 должен составлять не менее 20%.
должен составлять не менее 20%.
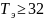 мкм.
мкм.
Из ГОСТ 25346-89 находим
допуски IT6… IT8. Для
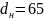 имеем следующие значения: IT6=19,
IT7=30,
IT8=46.
имеем следующие значения: IT6=19,
IT7=30,
IT8=46.
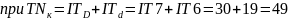 мкм
мкм
 мкм
– 69%
мкм
– 69%
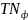
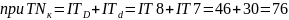 мкм
мкм
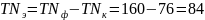 мкм
– 52%
мкм
– 52%
 мкм
мкм
 мкм
– 62,5%
мкм
– 62,5%
Пусть для вала 4 поле допуска IT6, а для зубчатого колеса 12 – IT7. Поправка U, учитывающая смятие неровностей контактных поверхностей:
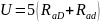 ,
,
где
 и
и
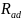 – среднее арифметическое отклонение
профиля отверстия и вала соответственно.
Из условия
– среднее арифметическое отклонение
профиля отверстия и вала соответственно.
Из условия
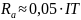 получаем:
получаем:
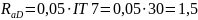 мкм,
мкм,
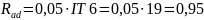 мкм,
мкм,
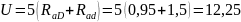 мкм,
мкм,
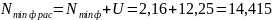 мкм,
мкм,
 мкм.
мкм.
Для обеспечения работоспособности посадки необходимо выполнение нижеуказанных условий:
а)
 ;
;
 ;
;
б)
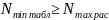 ;
;
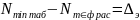 ;
;
в)
 .
.
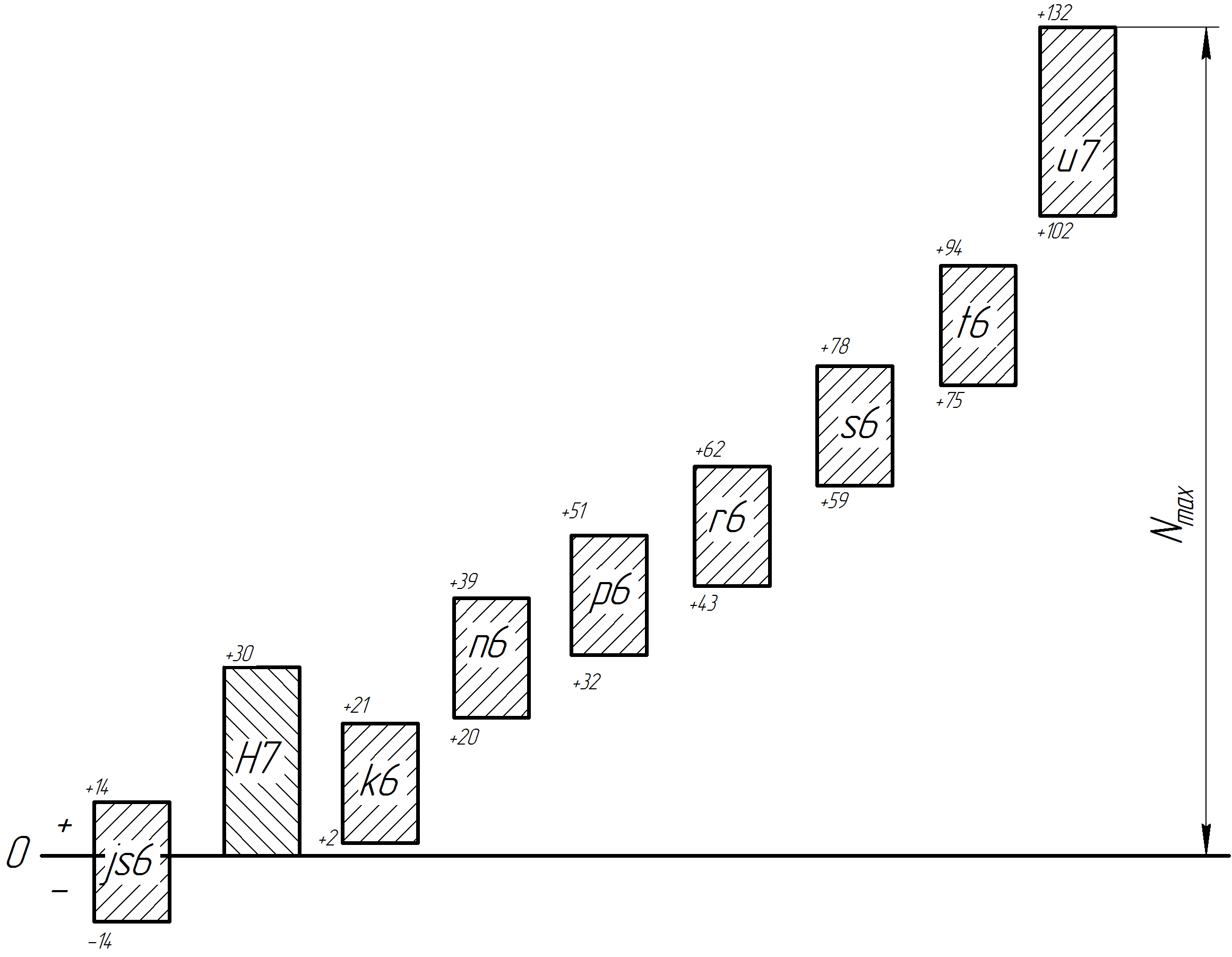
Рис. 1.1 Схема посадок с натягом
Из рисунка следует,
что гарантированный натяг мы имеем в
случае использования следующих посадок:
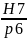 ,
,
 ,
,
 ,
,

Посадка |
|
|
|
|
65 |
51 |
2 |
162,546 |
2 2,165= 0,165 |
65 |
62 |
13 |
162,546 62=100 |
13 2=11 |
65 |
78 |
29 |
162,546 78=84 |
29 2=27 |
65 |
132 |
72 |
162,546 132=30 |
72 2=70 |
65 |
94 |
45 |
162,546 94=68 |
45 2=43 |
Таблица 1.2.
Всем условиям удовлетворяет посадка 65 .
Расчет переходной посадки.
По ГОСТ 25347-82 для сопряжения деталей 2-4 60 подбираем следующие посадки:
1)
60
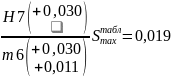 ;
;
2)
60
 ;
;
3)
60
 ;
;
4) 60 .
Если исходить из
того, что
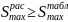 ,
а звёздочка имеет группу точности A, то
предпочтительной будет посадка 60
,
а звёздочка имеет группу точности A, то
предпочтительной будет посадка 60
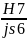 .
Для звёздочки группы точности A 120…260
мм, согласно ГОСТ 591-69, находим интервал
значений
.
Для звёздочки группы точности A 120…260
мм, согласно ГОСТ 591-69, находим интервал
значений
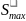 :
:
 мкм.
мкм.
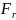 – значение
радиального биения по ГОСТ 591-69;
– значение
радиального биения по ГОСТ 591-69;
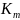 – коэффициент
пропорциональности.
– коэффициент
пропорциональности.
Находим средний размер отверстия и средний размер вала, для указанной выше посадки:
 мм;
мм;
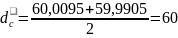 мм.
мм.
Построим схему посадки .
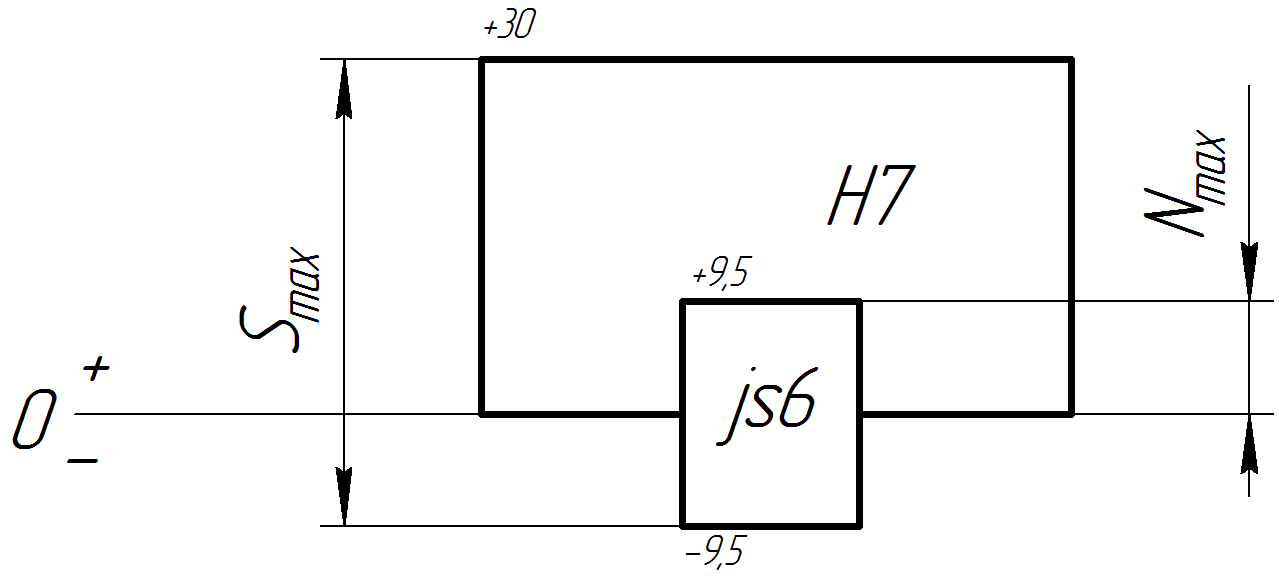
Рис. 2.1 Схема переходной посадки
Рассчитываем вероятность образования зазоров и натягов для посадки 60 :
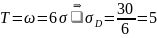 мкм;
мкм;
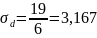 мкм.
мкм.
Среднее квадратичное отклонение распределения вероятностей образования зазоров и натягов в посадке будет равно:
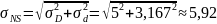 мкм.
мкм.
Средняя величина
зазоров в посадке составляет
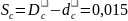 ,
т.е. 15 мкм. С учетом этого найдем вероятность
образования зазоров от 0 до
,
т.е. 15 мкм. С учетом этого найдем вероятность
образования зазоров от 0 до
 мкм.
мкм.

Максимальные значения вероятных зазоров и натягов, образование которых возможно в посадке, найдем с учетом того, что TD=0,030 мм, а Td=0,019 мм:
 ;
;
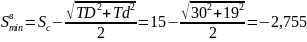 .
.
С помощью программы Mathcad построим график распределения вероятности образования зазоров и натягов в посадке вместо построения графика по семи точкам на основании формулы нормального распределения
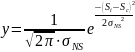 .
.
Функция dnorm (x, m, s) программы Mathcad возвращает плотность вероятности нормального распределения, где m и s есть среднее значение и среднее квадратичное отклонение соответственно.
Определяем диапазон рассеяния случайной величины:
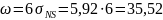 мкм.
мкм.
Предельные значения зазоров и натягов соответственно будут равны:
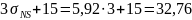 мкм;
мкм;
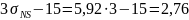 мкм.
мкм.
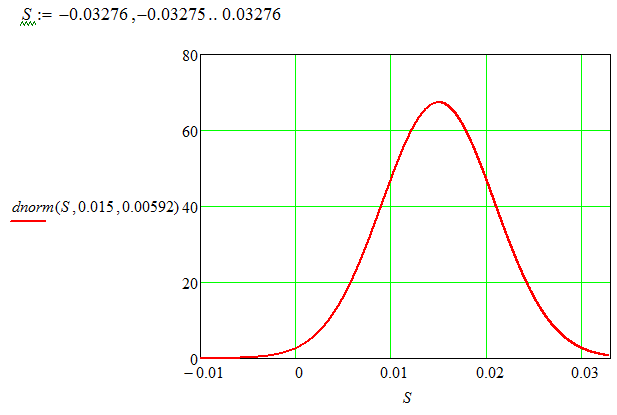
Рис. 2.2 График распределения вероятности образования зазоров и натягов, построенный с помощью программы Mathcad
С помощью Mathcad также находим значение функции
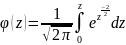
при
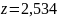 .
.
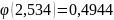
Построим соответствующий график, обозначив на нем штриховкой области, где вероятно получение зазоров до 15 мкм. Область вероятного получения натягов в посадке на графике расположена слева от оси ординат и ограничена кривой нормального распределения сверху и осью абсцисс снизу.
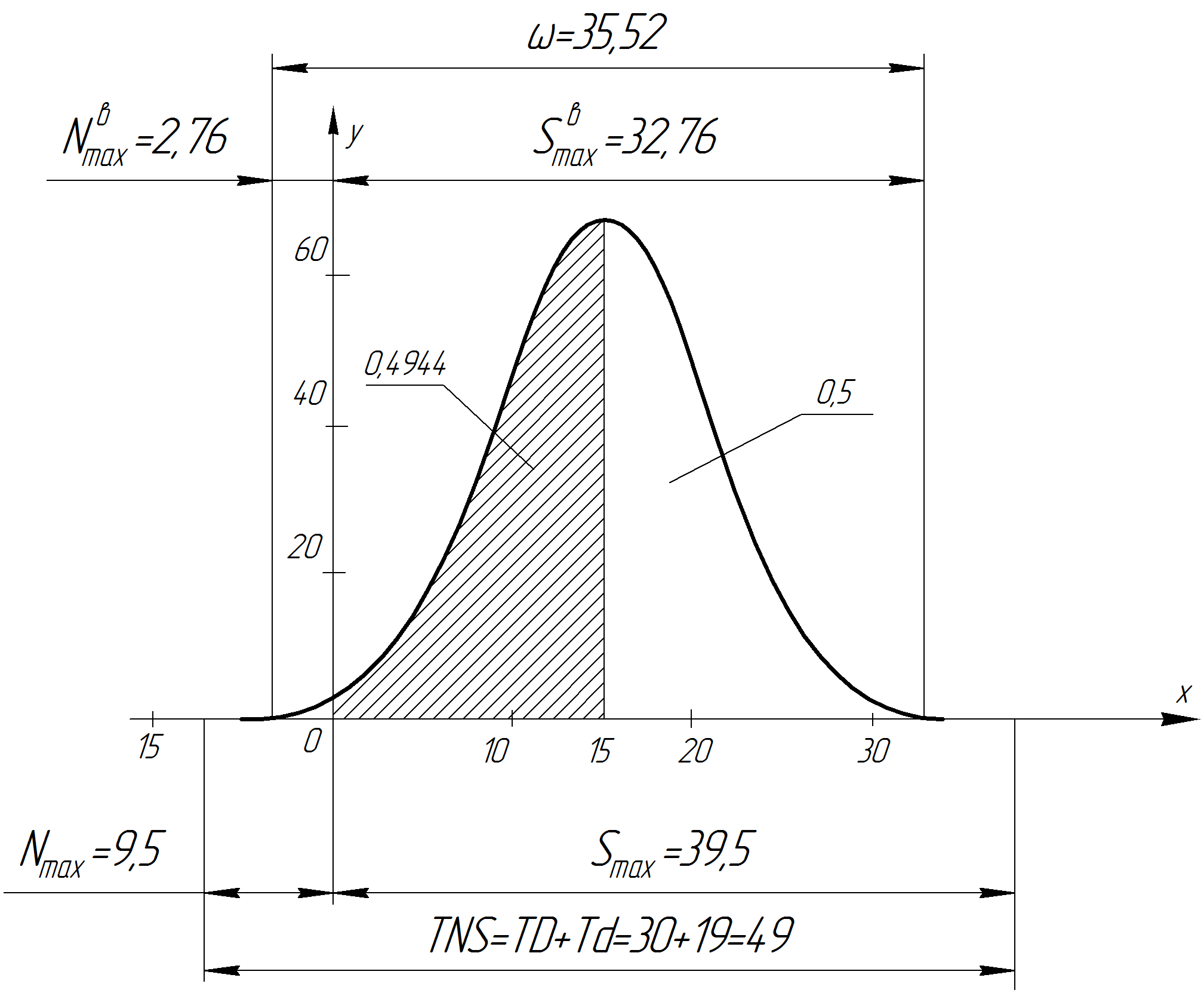
Рис. 2.3 График распределения вероятности образования
зазоров и натягов в посадке
Таким образом, вероятность образования зазора в посадке составляет более 99%. Вероятность образования натяга – менее 1%. Фактически, мы имеем посадку с гарантированным зазором.

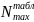
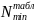
 51=111
51=111