Скачано с http://antigtu.ru
Задача Кузнецов Аналитическая геометрия
Условие задачи
Написать разложение вектора 
по векторам
Решение
Искомое разложение вектора 
имеет вид:
Или в виде системы:
Получаем: |
|
с |
|
|
|
К третьей строке приб вим первую: |
|
|
|
Скачано |
|
1-18
antigtu:
. |
ru |
Ко второй строке прибавим первую: |
|
antigtu |
||
|
|
|
||
|
Скачано |
с |
|
|
Искомое разложение: |
|
|
|
|
Задача Кузнецов Аналитическая геометрия 2-18 |
|
|||
Условие задачи |
|
|
|
|
Коллинеарны ли векторы и , построенные по векторам и |
? |
|||
Решение |
|
|
|
|
Векторы |
оллинеарны если существует такое число |
такое, что |
|
|
коллинеарны если их координаты пропорциональны. |
|
|
||
Нетрудно заметить, что |
|
для любых |
и . |
|
Т.е. |
, а значит векторы и - коллинеарны. |
|
||
. |
ru |
. Т.е. векторы
Задача Кузнецов Аналитическая геометрия 3-18
Условие задачи
Найти косинус угла между векторами |
и . |
antigtu |
|
Решение |
|
|
|
Найдем и : |
|
|
|
Находим косинус угла между векторами |
|
и : |
|
Скачано |
с |
|
|
|
|
|
|
Т.е. косинус угла: |
|
|
|
и следовательно угол
Задача Кузнецов Аналити еская геометрия 4-18
Условие з д чи
Вычислить площадь параллелограмма, построенного на векторах 
и 
.
. |
ru |
Решение |
|
|
|
. |
ru |
Площадь параллелограмма, построенного на векторах и |
, численно равна модулю их векторного |
||||
произведения: |
|
|
|
|
|
Вычисляем |
, используя его свойства векторного произведения: |
|
|
||
Вычисляем площадь: |
|
|
|
|
|
Т.е. площадь параллелограмма, построенного на векторах |
и равна . |
|
|
||
Задача Кузнецов Аналитическая геометрия 5-18antigtu |
|
|
|||
Скачано |
с |
|
|
|
|
Условие задачи |
|
|
|
|
|
Компланарны ли векторы , и ? |
|
|
|
||
Решение
Для того чтобы три вектора были компланарны (лежали в одной плоскости или параллельных
плоскостях), необходимо и достаточно, чтобы их смешанное произведение |
было равно |
|
нулю. |
|
|
Так как |
, то векторы , и компланарны. |
|
Согласно геометрическому смыслу векторного произведения:
Задача Кузнецов Аналитическая геометрия 6-18 |
|
|
||||
Условие задачи |
|
|
|
|
|
|
Вычислить объем тетраэдра с вершинами в точках |
и его высоту, опущенную из |
|||||
вершины |
на грань |
. |
|
|
. |
ru |
|
|
|
|
|
||
Решение |
|
|
|
|
|
|
Из вершины |
проведем векторы: |
|
|
|
|
|
В соответствии с геометрическим смыслом смешанного произведения имеем: |
|
|||||
|
|
|
с |
antigtu |
|
|
Вычислим смешанное произведение: |
|
|
|
|||
Скачано |
|
|
|
|||
|
|
|
|
|||
Вычислим векторное произведение: |
|
antigtu |
||
Объем тетраэдра: |
|
|
||
Получаем: |
|
|
|
|
Тогда: |
|
|
|
|
Высота: |
Скачано |
с |
|
|
|
|
|||
|
|
|
||
Задача Кузнецов Аналитическая геометрия 7-18 |
||||
Условие задачи |
|
|
|
|
Найти расстояние от точки |
до плоскости, проходящей через три точки |
|||
Решение
Находим ур внение плоскости, проходящей через три точки
Проведем преобразования:
. |
ru |
.
:
|
|
|
|
antigtu |
. |
ru |
|
Расстояние от точки |
|
|
|
|
|||
до плоскости |
|
: |
|
||||
Находим: |
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
Задача Кузнецов Аналитическая геометрия 8-18 |
|
|
|
||||
|
Скачано |
|
|
|
|
|
|
Условие задачи |
|
|
|
|
|
|
|
Написать уравнение плоскости, пр х дящей через точку перпендикулярно вектору |
. |
||||||
Решение |
|
|
|
|
|
|
|
Найдем вектор |
: |
|
|
|
|
|
|
Так как ве тор |
перпендикулярен искомой плоскости, то его можно взять в качестве вектора |
||||||
нормали. Поэтому уравнение плоскости будет иметь вид:
Задача Кузнецов Аналитическая геометрия 9-18
Условие задачи
Найти угол между плоскостями:
Решение |
antigtu |
Двугранный угол между плоскостями равен углу между их нормальными векторы заданных плоскостей:
Угол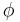 
между плоскостями определяется формулой:
|
Скачано |
с |
||
Задача Кузнецов Аналитическая ге метрия 10-18 |
||||
Условие задачи |
|
|
|
|
Найти координаты точки |
|
, рав оудале ой от точек и . |
||
Решение |
|
|
|
|
Найдем расстояние |
и |
: |
|
|
Так как по условию задачи |
|
, то |
||
. |
ru |
векторами. Нормальные
Таким образом |
. |
antigtu |
. |
ru |
|
|
Задача Кузнецов Аналитическая геометрия 11-18
Условие задачи
Пусть 
- коэффициент преобразования подобия с центром в начале координат. Верно ли, что точка 
принадлежит образу плоскости 
?
Решение |
|
|
с |
При преобразовании подобия с центром в начале координат плоскость |
|||
|
и коэффициентом переходит в плоскость |
||
|
Скачано |
. |
Находим образ плоскости : |
|
|
||
Подставим координаты точки в урав е ие : |
|||
Так как |
, то то ка принадлежит образу плоскости . |
||
Задача Кузнецов Ан литическая геометрия 12-18
Условие задачи
Написать канонические уравнения прямой.
Решение |
|
|
|
ru |
Канонические уравнения прямой: |
antigtu |
. |
|
|
|
, |
|
||
|
|
|
||
где |
- координаты какой-либо точки прямой, а |
- ее направляющий |
||
вектор.
Так как прямая принадлежит одновременно обеим плоскостям, то ее направляющий вектор 
ортогонален нормальным векторам обеих плоскостей. Нормальные вектора плоскостей:
Найдем направляющий вектор 
:
Скачано |
с |
. Пусть , тогда |
Найдем какую-либо точку прям й |
|