Практическое занятие №2 Расчет электрической цепи методом контурных токов

П.2.1. Дана электрическая цепь рис.П.2 и параметры элементов цепи:

[Ом] [В]

Необходимо найти токи ветвей электрической цепи методом контурных токов (номера контуров обозначены на рис.П.2).

Рис. П.2. Пример электрической цепи для расчета.

П.2.2. Запишем систему уравнений в матричной форме

.

После подстановки значений параметров элементов получим

.

П.2.3. Решаем систему уравнений по методу Крамера

,

для чего необходимо вычислить четыре детерминанта. Детерминанты матрицы системы уравнений находим с помощью программы Excel

В результате получаем значения контурных токов:

[А]

Применяя подстановки Максвелла, получаем значения токов ветвей электрической цепи рис.П.2:

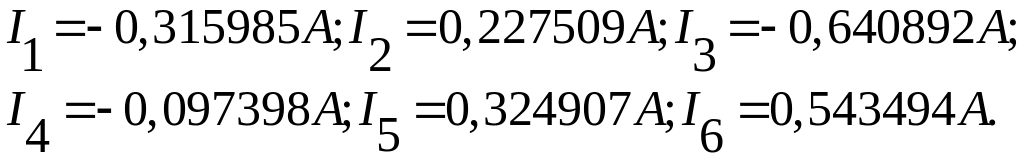
П.2.4. Повторим расчет, изменив параметр одного элемента: В.

Практическое занятие № 3. Расчет тока ветви электрической цепи методом эквивалентного генератора.

П.3.1. Найдем значение тока в первой ветви электрической цепи рис.П.2 методом эквивалентного генератора для чего выделим ветвь с помощью сечения, рис. П.3.

Рис.П.3. Подготовка схемы для расчета тока .

Большую часть электрической цепи рис.П.3 представим активным двухполюсником, а затем эквивалентным генератором, рис. П.4.

Рис. П.4. Эквивалентная замена активного двухполюсника.

П.3.2. Найдем параметры эквивалентного генератора , . Найдем величину эквивалентного сопротивления между внешними узлами 1 и 2, для чего контур из ветвей 3, 4, 5 заменим эквивалентной звездой с лучами 34, 35, 45:

Ом,

Ом,

Ом.

Запишем выражение для определения величины эквивалентного сопротивления:

Ом.

Найдем номинал эквивалентного источника ЭДС , для чего составим систему уравнений методом контурных токов для большей части электрической цепи рис.П.3:

.

Или после подстановки числовых данных

.

Найдем значения детерминант

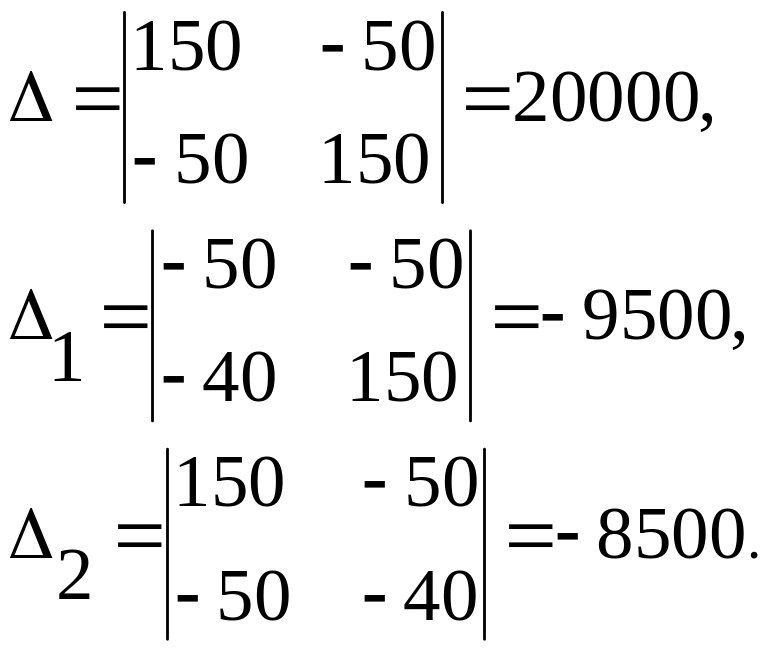
и значения контурных токов

[А]

Итак, получаем токи ветвей

[А]

Продвигаясь вслед за стрелкой тока, составим следующие уравнения:

После подстановки одного уравнения в другое получим

В

напряжение холостого хода, а, следовательно, номинал источника ЭДС, стрелка которого ориентирована на узел 1. Теперь большая часть электрической цепи рис.П.3 может быть заменена ветвью, содержащей эквивалентное сопротивление 47,249999 Ом и эквивалентный источник ЭДС

11,25 В.

П.3.3. Соединяем одноименные узлы ветви 1 и эквивалентного генератора, соблюдая ориентацию стрелки источника ЭДС в сторону узла 1. Определяем ток ветви в полученном контуре:

А.

П.3.4. Повторить вычисления для тока .

Практическое занятие №4 Расчет простой цепи переменного тока.

П.4.1. Дана простая электрическая цепь

Рис. П.5. Ветвь цепи переменного тока.

и параметры элементов: мкФ, Ом; напряжение ветви В.

П.4.2. Найдем ток ветви, для чего вычислим модуль комплексного сопротивления

Модуль комплексного сопротивления ветви будет равен

Ом.

Тогда ток ветви можно определить по закону Ома

мА.

П.4.3. Определим напряжения на элементах ветви.

В.;

В.

Проверка.

В.

П.4.4. Повторить расчет, предварительно изменив параметр активного сопротивления Ом .