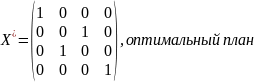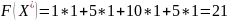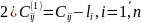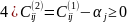- •Задача целочисленного программирования (зцп)
- •Метод Гомори
- •Ι. Полностью целочисленные задачи:
- •Комбинаторные методы: метод ветвей и границ
- •Транспортная задача по критерию стоимости в матричной постановке
- •Методы решения транспортной задачи
- •Игра 2-х участников с нулевой суммой.
- •- Седловая точка
- •Приведение матричной игры к задаче линейного программирования (злп).
- •Задачи теории статистических решений (тср).
- •Кооперативные игры
Методы решения транспортной задачи
Метод потенциалов
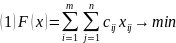 двойственные переменные
двойственные переменные
(2a) |
…
|
= =
= |
|
(2b) |
…
|
= =
= |
|
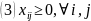
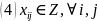
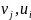 -
локальные поясные цены (при наценке и
единой цене), обеспечивающие правильное
направление перевозок
-
локальные поясные цены (при наценке и
единой цене), обеспечивающие правильное
направление перевозок
Двойственная задача
|
|
|
Для заполненных клеток
|
|
|
Для не заполненных клеток
|
|
|
|
|
|
Если
обозначить
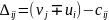 ,
для
,
то план оптимален, если
,
для
,
то план оптимален, если
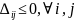
Пример:
|
|
50 |
60 |
90 |
||||
|
|
|
||||||
m+n-1=2+3-1=4 |
150 |
|
501 |
604 |
402 |
|||
|
50 |
|
31 |
2-3 |
503 |
|||
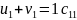

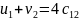
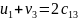

Тарифы
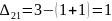
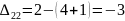
План не оптимален
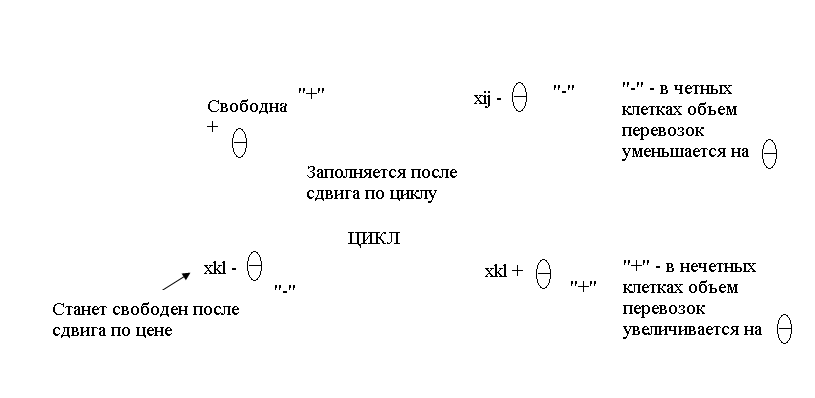
Переход от одного опорного решения к другому
для любой свободной клетки таблицы, содержащей опорное решение, существует единственный цикл, содержащий эту клетку и часть клеток, занятых опорным решением.
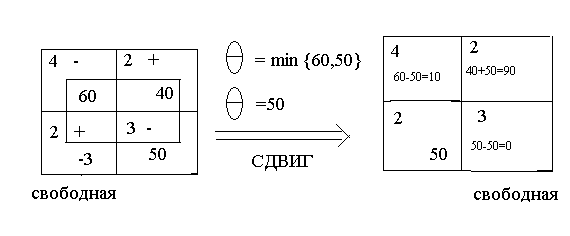
Если таблица содержала опорное решение, при сдвиге на
 по любому циклу, содержащему одну
свободную клетку, получим опорное
решение.
по любому циклу, содержащему одну
свободную клетку, получим опорное
решение.

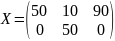
Критерий оптимальности:
Если
перевозка осуществляется, то цена в
пункте потребления
 равна
цене в пункте производства
равна
цене в пункте производства
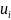 плюс
транспортные затраты
плюс
транспортные затраты
2.Распределительный метод
строится опорный план ТЗ
для каждой свободной клетки строят цикл (единственный)
для каждой клетки (l,k) находят
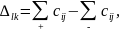
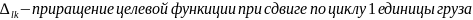
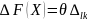
опорное решение можно улучшить, если
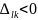
Если
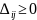 (для
любых свободных клеток) - план
оптимален
(для
любых свободных клеток) - план
оптимален
3.Метод дифференциальных рент
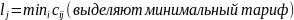
Заполняются клетки с выделенным
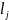
В избыточных строках (+) запасы не распределены; в не заставленных не удовлетворены все потребности
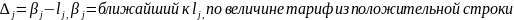
min Δj= Δ- промежуточная рента
к тарифам отрицательных строк добавляют Δ
в новой таблице заполняют строки(столбцы) с одной заполненной клеткой и вычисляют:
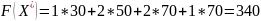
|
ai\bj |
b1=80 |
b2=70 |
b3=70 |
Избыток/недостаток |
+1 |
|||||||||||
Запас распределен → |
а1 = 100 |
80 1 |
20 2 |
4 |
- 50 |
||||||||||||
Запас не распределен→ |
а2 = 120 |
2 |
4 |
70 |
+50 |
||||||||||||
|
Δj разность |
1 |
2 |
- |
min Δj= Δ=1 |
||||||||||||
|
|
||||||||||||||||
|
ai\bj |
80 |
70 |
70 |
|
|
|
|
|
|
|||||||
|
100 |
30 2 |
70 3 |
5 |
|
|
|
|
|
|
|||||||
|
120 |
50 2 |
4 |
70 1 |
|
|
|
|
|
|
|||||||
Все
запасы распределены: 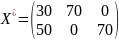
4.«Венгерский» метод
(применяется, например, для решения ТЗ о назначениях транспортного типа)
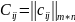
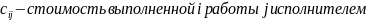
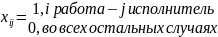
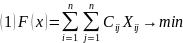
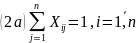
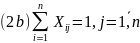
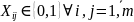
В
|
5) отмечают «независимые 0»(в разных строчках и столбцах) |

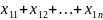
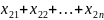
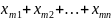
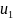
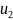
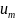
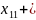
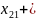 …
…
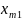

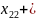
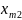
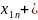
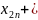
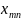
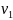


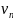
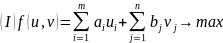
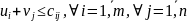
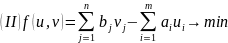
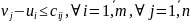
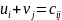
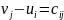
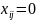
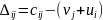

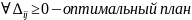
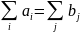 =200
=200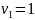
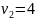
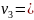 2
2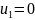

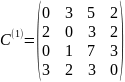
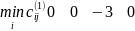
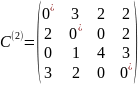
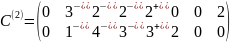
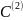 проводят
минимальное число горизонтальных и
вертикальных прямых, чтобы вычеркнуть
в матрице все нулевые элементы
проводят
минимальное число горизонтальных и
вертикальных прямых, чтобы вычеркнуть
в матрице все нулевые элементы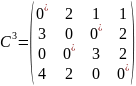
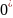 заменяют
на 1, а все остальные на 1
заменяют
на 1, а все остальные на 1