Вопрос 17) Теорема Безу. Остаток от деления многочлена f(X) на линейный двучлен X–a равен значению многочлена в точке а, т. Е. Числу f(a).
Доказательство.Разделим F(x) на x–a с остатком, т. е. представим его в виде Как было сказано выше, остаток R является константой. Подставим x=a : что и требовалось доказать.
Следствие.
Для того чтобы многочлен F(x) делился
на двучлен x–a, необходимо и достаточно,
чтобы F(a)=0, т. е. чтобы а было корнем
многочлена x.
Схема
Горнера - способ деления многочлена 
на
бином 
.
Работать придётся с таблицей, первая
строка которой содержит коэффициенты
заданного многочлена. Первым элементом
второй строки будет число а, взятое
из бинома
:
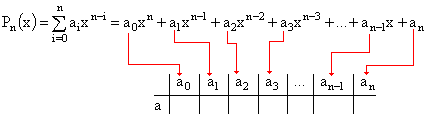
После
деления многочлена n-ой степени на
бином
,
получим многочлен, степень которого на
единицу меньше исходного, т.е. равна 
Вопрос 18) Основна́я теоре́ма а́лгебры-Всякий отличный от константы многочлен (от одной переменной) с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
Доказательсво: Самое простое доказательство этой теоремы даётся методами комплексного анализа. Используется тот факт, что функция, аналитическая на всей комплексной плоскости и не имеющая особенностей на бесконечности, есть константа. Посему, функция 1/p, где p — многочлен, должна иметь хоть один полюс на комплексной плоскости, а, соответственно, многочлен имеет хоть один корень
Следствие: Немедленным следствием из теоремы является то, что любой многочлен степени над полем комплексных чисел имеет в нём ровно корней, с учётом кратности корней.
Вопрос 19) Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни.
Если 
—
корни многочлена
(каждый
корень взят соответствующее его кратности
число раз), то коэффициенты 
выражаются
в виде симметрических
многочленов от
корней, а именно:
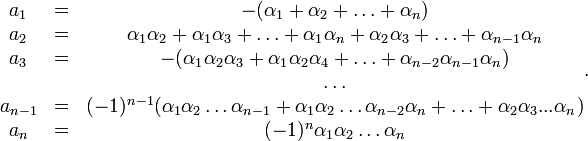
Иначе
говоря 
равно
сумме всех возможных произведений
из 
корней.
Если
старший коэффициент многочлена 
,
то для применения формулы Виета необходимо
предварительно разделить все коэффициенты
на 
(это
не влияет на значение корней многочлена).
В этом случае формула Виета дают выражение
для отношений всех коэффициентов к
старшему. Из последней формулы Виета
следует, что если корни многочлена
целочисленные, то они являются делителями
его свободного члена, который также
целочисленен.
Вопрос 20) Рациональной дробью(рациональной функцией) называется отношением двух многочленом . Рациональная дробь называется правильной, если степень многочлена P(x) меньше степени многочлена Q(x), в противном случае – неправильной
Покажем, что всякую правильную рациональную дробь можно разложить на сумму простейших дробей.
Пусть
дана правильная рациональная дробь 
.
Причём последовательное применение данной теоремы ко второму слагаемому данной теоремы приводит:
(2-134)
Где
многочлен,
степень которого ниже степени знаменателя.
И аналогично формуле (2-134) можно получить:
.