Вопрос13) Однородной слау называется система, все правые части которой равны нулю одновременно

Теорема (о структуре общего решения). Пусть  , тогда:

• если  , где   — число переменных системы, то существует только тривиальное решение;

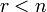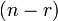• если  , то существует   линейно независимых решений рассматриваемой системы: 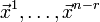 , причём её общее решение имеет вид: 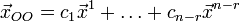 , где 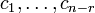  — некоторые константы.

Вопрос 14) Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы

^{Вопрос 15)} Структура общего решения неоднородной системы уравнений

Рассмотрим неоднородную систему   и соответствующую ей однородную систему  . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.

Свойства решений неоднородной системы уравнений

1. Разность двух решений   и   неоднородной системы есть решение однородной системы.

Действительно, из равенств   и   следует, что  .

2. Пусть   — решение неоднородной системы. Тогда любое решение   неоднородной системы можно представить в виде

, где   — решение однородной системы.

В самом деле, для любого решения   неоднородной системы разность   по свойству 1 является решением однородной системы, т.е.   — решение однородной системы.

Теорема 5.4 о структуре общего решения неоднородной системы.

Пусть   — решение неоднородной системы, а   — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец

(5.15)

при любых значениях [i]произвольных постоянных   является решением неоднородной системы, и, наоборот, для каждого решения   этой системы найдутся такие значения произвольных постоянных  , при которых это решение   удовлетворяет равенству (5.15).[/i]

Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.

Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.

Вопрос 16) Многочленом называется рациональное выражение, в котором над переменной величиной производятся только действия сложения, вычитания и умножения

Определение. Два многочлена P(x) и Q(x) относительно х с любыми действительными коэффициентами будем считать равными P(x) = Q(x) лишь в том случае, если равны их коэффициенты при одинаковых степенях х.

Значения таких многочленов очевидно равны. Существует утверждение обратное этому: если значения двух многочленов равны при всех значениях х , то такие многочлены равны, их коэффициенты совпадают при одинаковых степенях х.

Многочлены можно складывать. Суммой двух многочленов P(x) и Q(x) называется многочлен, у которого коэффициент при каждой степени х равен сумме коэффициентов при той же степени в многочленах P(x) и Q(x).

Многочлены можно вычитать. Разностью двух многочленов P(x) и Q(x) называется многочлен, у которого коэффициент при каждой степени х равен разности коэффициентов при той же степени в многочленах P(x) и Q(x).

Многочлены можно умножать. Чтобы умножить два многочлена P(x) и Q(x), нужно каждый член многочлена P(x) умножить на каждый член многочлена Q(x) и полученные результаты сложить.

Сложение, умножение и вычитание многочленов – основные арифметические действия над многочленами.

Пусть P(x) = Q(x)S(x), P(x) и Q(x) два многочлена, причем степень многочлена P(x) не меньше степени многочлена Q(x) и, если существует такой многочлен S(x), что выполняется равенство

P(x) = Q(x)S(x), то говорят, что многочлен P(x) делится нацело на многочлен Q(x). P(x), Q(x), S(x) называются соответственно делимое, делитель, частное. Если такого многочлена не существует, то многочлен P(x) не делится на Q(x). В этом случае, как и при рассмотрении деления с числами производится деление с остатком.

Разделить многочлен P(x) на Q(x) с остатком это значит представить многочлен P(x) в виде равенства P(x) = Q(x)S(x) + R(x), где R(x) остаток, причём степень R(x) меньше степени Q(x).При делении многочленов с остатком справедлива следующая теорема.

Для любых двух многочленов P(x) и Q(x) всегда можно найти и притом однозначно два многочлена S(x) и R(x), для которых справедливо равенство P(x) = Q(x)S(x) + R(x).

Деление двух многочленов осуществляется углом.